Закон распределения данных, точечные оценки параметров
Законом распределением случайной величины называют соответствие между возможными значениями и их вероятностями.
Точечное оценивание - это вид статистического оценивания, при котором значение неизвестного параметра q приближается отдельным числом.
Суть точечного оценивания в том, что для τq строится одна статистика t(x) = τ, которая принимается за оценку τq, т.е. t(x) = τ
«Хорошей» оценкой является такая оценка, которая наиболее близка к истинному значению τq, т.е. когда ее значения в каком-то смысле сконцентрированы вокруг истинного значения τq [1]
Задача точечного оценивания
Исследуется случайная величина X, распределение которой относится к параметрическому множеству Fq (x), где q (q1,..., qk) – неизвестный k-мерный параметр.
Имеется выборка наблюденных значений случайной величины Fq (x): τ = τ (q) oбъема выборки n. Требуется построить точечную оценку (статистику) для данной функции τ = τ (q) и исследовать качество данной оценки.
Cвойства точечных оценок t=t(x)
a) Несмещенность: Et(x) = t(q) (EX – математическое ожидание случайной величины Fn(x)) или асимптотическая несмещенность Et(x) ¾¾¾®t(q), при n®¥ [2].
б) Состоятельность: Одно из самых очевидных требований к точечной оценке заключается в том, чтобы можно было ожидать достаточно хорошего приближения к истинному значению параметра при достаточно больших значениях объема выборки n. Это означает, что оценка t(x) должна сходиться к истинному значению t(q) при n®¥. Это свойство оценки и называется состоятельностью. Поскольку речь идет о случайных величинах, для которых имеются разные виды сходимости, то и данное свойство может быть точно сформулировано по-разному:
- если t(x) сходится к истинному значению t(q) с вероятностью 1 (почти наверное), то тогда оценка называется сильно состоятельной;
- если имеет место сходимость по вероятности, то тогда оценка называется слабо состоятельной.
Условие состоятельности является практически обязательным для всех используемых на практике оценок. Несостоятельные оценки используются крайне редко [1].
в) Эффективность несмещенной оценки характеризуется дисперсией Dt(x) и используется для сравнения качества несмещенных оценок.
Одновременное выполнение этих желательных свойств не всегда возможно, поэтому представление о «хорошей» оценке зависит от цели и возможностей исследования, определяющих приоритетные свойства оценки. Так, для малых выборок часто важна несмещенность оценки, а для больших – асимптотическая несмещенность и состоятельность. А иногда, сознательно отказываясь от одних свойств оценок, добиваются выполнения других, более важных с точки зрения исследования свойств.
Интервальная оценка среднего
Интервальное оценивание — один из видов статистического оценивания, предполагающий построение интервала, в котором с некоторой вероятностью находится истинное значение оцениваемого параметра. [2].

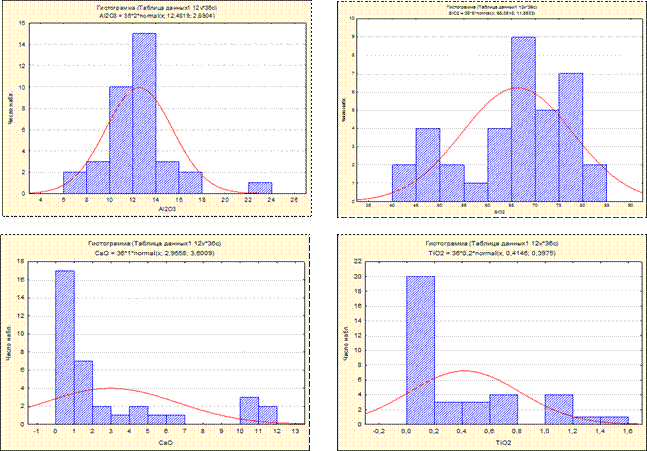

Рисунок 2. Гистограммы по переменным
Корреляционный анализ
Метод обработки статистических данных, заключающийся в изучении коэффициентов корреляции между переменными.
При этом сравниваются коэффициенты корреляции между одной парой или множеством пар признаков для установления между ними статистических взаимосвязей.
Корреляционный анализ применяется только для анализа связи количественных и/или качественных порядковых признаков.
Корреляция линейная - англ. correlation, linear; Корреляция, при которой отношение степени изменения одной переменной к степени изменения другой переменной является постоянной величиной.
Корреляционный момент. Для прерывных случайных величин корреляционный момент выражается формулой 
а для непрерывных – формулой 
Корреляционный момент есть характеристика системы случайных величин, описывающая, помимо, рассеивания величин  и
и  , еще и связь между ними.
, еще и связь между ними.
Коэффициент корреляции Пирсона (r-Пирсона) применяется для исследования взаимосвязи двух переменных, измеренных в метрических шкалах на одной и той же выборке. Он позволяет определить, насколько пропорциональная изменчивость двух переменных.
Данный коэффициент разработали Карл Пирсон, Фрэнсис Эджуорт и Рафаэль Уэлдон в 90-х годах XIX века. Коэффициент корреляции изменяется в пределах от минус единицы до плюс единицы. [7]
Коэффициент корреляции r-Пирсона характеризует существование линейной связи между двумя величинами. Если связь криволинейная то он не будет работать.
Чтобы приступать к расчетам коэффициента корреляции r-Пирсона необходимо выполнение следующих условий:
- Исследуемые переменные X и Y должны быть распределены нормально.
- Исследуемые переменные X и Y должны быть измерены в интервальной шкале или шкале отношений.
- Количество значений в исследуемых переменных X и Y должно быть одинаковым.
При расчете коэффициент линейной корреляции Пирсона используется специальная формула. Величина коэффициента корреляции варьируется от 0 до 1.
Слабыми сторонами линейного коэффициента корреляции Пирсонаявляются:
- Неустойчивость к выбросам.
- С помощью коэффициента корреляции Пирсона можно определить только силу линейной взаимосвязи между переменными, другие виды взаимосвязей выявляются методами регрессионного анализа. [6]
Обработав исходные данные удалось получить таблицу корреляции Таблица №4. Обработав полученные данные удалось проследить зависимость разных элементов друг от друга, диаграммы рессеяния с зависимостью указаны на рисунке № 3. Диаграммы рассеяния – это вид графического отображения данных, когда каждое наблюдение изображается точкой на координатной плоскости, где оси соответствуют переменным (X - горизонтальной, а Y - вертикальной оси). Диаграмма рассеяния визуализирует зависимость между двумя переменными X и Y
Таблица №4
Таблица корреляционного анализа


Рисунок 3. Диаграммы рассеяния
Регрессионный анализ
В линейный регрессионный анализ входит широкий круг задач, связанных с построением (восстановлением) зависимостей между группами числовых переменных x=(x1,…,xk) и y=(y1,…,yk).
Предполагается, что X - независимые переменные (предикторы, объясняющие переменные) влияют на значения Y - зависимых переменных (откликов, объясняемых переменных). По имеющимся эмпирическим данным (X_i,Y_i)i=1,…,n требуется построить функцию ∫ (X), которая приближенно описывала бы изменение Y при изменении X: y ≈f(x)
Предполагается, что множество допустимых функций, из которого подбирается ∫〖(X)〗 является параметрическим: ∫〖(X)〗=f(x,θ)
где - θ неизвестный параметр (вообще говоря, многомерный). При построении ∫〖(X)〗 будем считать, что y=f(x,θ)+ε
где первое слагаемое – закономерное изменение Y от X, а второе -ε - случайная составляющая с нулевым средним; f(x,θ) является условным математическим ожиданием Y при условии известного X и называется регрессией Y по X.
Пусть n раз измерены значения факторов x_1,…,x_k и соответствующие значения переменной y; предполагается, что y_(i)= β_0+β_(ix_ij)+⋯+β_k β_ik+ε_i,i=1,…,n
(второй индекс у x относится к номеру фактора, а первый – к номеру наблюдения); предполагается также, что Mε_i=0, Mε_i^2=0^2
M(ε_i ε_j)=0, i≠j
т.е. ε_i- некоррелированные случайные величины. Соотношения (2) удобно записывать в матричной форме: y=xβ+ε
где y=(y_1,…,y_k) вектор-столбец значений зависимой переменной, t - символ транспонирования, β=(β_0,β_1,…,β_k вектор-столбец (размерности k) неизвестных коэффициентов регрессии,ε=(ε_1,…,ε_n) - вектор случайных отклонений,
-матрица n×(k+1); в i-й строке (1,x_ij,…,x_jk) находятся значения независимых переменных в i-м наблюдении первая переменная – константа, равная 1.
Построим оценку β для вектора β так, чтобы вектор оценок y=xβ зависимой переменной минимально (в смысле квадрата нормы разности) отличался от вектора заданных значений: ‖y-y‖^2=‖y-xβ‖^2→min no β. [5]
Решением является (если ранг матрицы X равен k+1 оценка
β=(x^i x) x^i y
Нетрудно проверить, что она несмещенная.
Множественная линейная регрессия предполагает линейную связь между переменными в уравнении, и нормальным распределением остатков. Если эти предположения нарушаются, окончательные заключения могут оказаться неточными. Нормальный вероятностный график остатков наглядно показывает наличие или отсутствие больших отклонений от высказанных предположений.
Таблица №5
Таблица описательных статистики


Рисунок 4. Нормальный вероятностный график остатков
Кластерный анализ
Кластерный анализ — это общий термин для целого ряда методов, используемых для группировки объектов, событий или индивидов в классы (кластеры) на основе сходства их характерных признаков. Несмотря на отсутствие единого определения кластера, во всех его определениях особо подчеркиваются такие условия, как сходство, однородность и близость. Если воспользоваться специальной терминологией, то кластеры можно определить, как однородные подгруппы, формируемые методом, который минимизирует дисперсию внутри групп (кластеров) и максимизирует дисперсию между группами.
Методики кластеризации используются для установления сходных подгрупп объектов или индивидов и для построения таксономии. Таким образом, они помогают исследователю в описании структуры совокупности объектов и отношений между ними, а также в формулировании законов и утверждений относительно классов объектов.
Если обобщить различные классификации методов кластеризации, то можно выделить ряд групп (некоторые методы можно отнести сразу к нескольким группам и потому предлагается рассматривать данную типизацию как некоторое приближение к реальной классификации методов кластеризации): [8]
1. Вероятностный подход. Предполагается, что каждый рассматриваемый объект относится к одному из k классов.
• K-средних (K-means)
• K-medians
• EM-алгоритм
• Алгоритмы семейства FOREL
• Дискриминантный анализ
2. Подходы на основе систем искусственного интеллекта. Весьма условная группа, так как методов AI очень много и методически они весьма различны.
• Метод нечеткой кластеризации C-средних (C-means)
• Нейронная сеть Кохонена
• Генетический алгоритм
3. Логический подход. Построение дендрограммы осуществляется с помощью дерева решений.
4. Теоретико-графовый подход.
• Графовые алгоритмы кластеризации
5. Иерархический подход. Предполагается наличие вложенных групп (кластеров различного порядка). Алгоритмы в свою очередь подразделяются на агломеративные (объединительные) и дивизивные (разделяющие). По количеству признаков иногда выделяют монотетические и политетические методы классификации.
• Иерархическая дивизивная кластеризация или таксономия. Задачи кластеризации рассматриваются в количественной таксономии.
6. Другие методы. Не вошедшие в предыдущие группы.
Статистические алгоритмы кластеризации, ансамбль кластеризаторов, алгоритмы, семейства KRAB,алгоритм, основанный на методе просеивания,DBSCAN и др.
Подходы 4 и 5 иногда объединяют под названием структурного или геометрического подхода, обладающего большей формализованностью понятия близости[9]. Несмотря на значительные различия между перечисленными методами все они опираются на исходную «гипотезу компактности»: в пространстве объектов все близкие объекты должны относиться к одному кластеру, а все различные объекты соответственно должны находиться в различных кластерах.
Все методы кластерного анализа состоят из четырех основных шагов: а) выбор мер и произведение измерений характерных признаков объектов или индивидов, подлежащих классификации; б) задание меры сходства; в) формулирование правил и определение порядка формирования кластеров; г) применение этих правил к данным для формирования кластеров. Так как каждый шаг предполагает выбор из множества возможных процедур, был разработан широкий спектр методик кластеризации.
На первом шаге принимается решение о том, какие характерные признаки или свойства будут использоваться в качестве основы классификации. Конечно, это решение будет зависеть от проблемы исследования и природы классифицируемых объектов. Хотя обычно все признаки имеют одинаковые веса, не исключается возможность выбора процедуры приписывания различных весов.
Принимаемое на втором шаге решение связано с выбором подходящей меры сходства. Это м. б. число общих признаков, корреляция между признаками, метрика (пространства классификации) или к.-л. др. мера.
На третьем шаге выбирается сам метод классификации. Агломеративные методы начинают с анализа отдельных объектов или индивидов и объединяют их в группы; методы расслоения начинают с анализа полной группы и делят ее на подгруппы. Классификация по одному признаку приводят к классам, все элементы которых имеют по крайней мере один общий отличительный признак; классификация, основывается на сравнении нескольких признаков, приводят к группам, которые обладают рядом общих свойств, но не обязательно обладают одним общим отличительным признаком.
Принимаемое на четвертом шаге решение касается момента остановки процедуры классификации или, проще говоря, определения количества сформированных групп. Это может определяться как внутренними критериями (например, естественным разбиением полной группы на подгруппы), так и внешними критериями (т. е. тем, какая схема классификации приводит к наиболее полезным закономерностям).
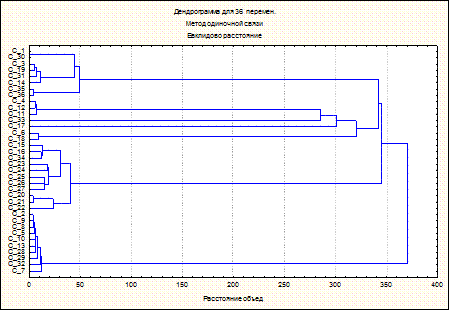 |
Рисунок 5.1. Дендрограмма переменных по элементам

Рисунок 5.2. Дендрограмма переменных по скважинам

Рисунок 6. График средних для каждого кластера

Таблица №6
Таблица средних кластеров
| Кластер 1 | Кластер 2 | |
| C_1 | 63,388 | 3,282636 |
| C_2 | 68,361 | 2,749 |
| C_3 | 78,163 | 1,935091 |
| C_4 | 68,773 | 2,733909 |
| C_5 | 67,582 | 2,869273 |
| C_6 | 73,616 | 2,273727 |
| C_7 | 64,755 | 3,143909 |
| C_8 | 67,841 | 2,821909 |
| C_9 | 68,026 | 2,787727 |
| C_10 | 71,577 | 2,572 |
| C_11 | 65,345 | 3,037091 |
| C_12 | 69,715 | 2,677546 |
| C_13 | 70,425 | 2,586273 |
| C_14 | 82,473 | 1,567364 |
| C_15 | 45,514 | 4,834363 |
| C_16 | 43,399 | 5,017091 |
| C_17 | 44,512 | 4,940273 |
| C_18 | 76,427 | 2,047091 |
| C_19 | 79,214 | 1,785455 |
| C_20 | 77,372 | 2,071545 |
| C_21 | 77,514 | 2,026454 |
| C_22 | 83,728 | 1,475636 |
| C_23 | 51,755 | 4,314909 |
| C_24 | 53,758 | 4,180909 |
| C_25 | 65,769 | 3,150909 |
| C_26 | 62,19 | 3,286273 |
| C_27 | 58,636 | 3,648182 |
| C_28 | 72,282 | 2,442182 |
| C_29 | 74,369 | 2,27 |
| C_30 | 63,388 | 3,282636 |
| C_31 | 78,462 | 1,850182 |
| C_32 | 68,182 | 2,779818 |
| C_33 | 78,106 | 2,069818 |
| C_34 | 46,686 | 4,745364 |
| C_35 | 48,777 | 4,665182 |
| C_36 | 47,776 | 4,767364 |
Факторный анализ
С возрастанием количества анализируемых признаков быстро растет трудность изучения и классификации характеризуемых ими объектов. Между тем, любые сложнопостроенные системы, как правило, управляются сравнительно небольшим набором факторов. Выявлению и анализу этих факторов посвящен широкий круг вычислительных процедур, обычно объединяемых названием «факторный анализ». Следует однако, помнить, что в названной области выделяется несколько самостоятельных процедур: метод главных компонент (МГК), R–метод факторного анализа, Q–метод факторного анализа, анализ главных координат, анализ соответствия. Все эти методы основаны на выделении собственных значений и собственных векторов ковариационной или корреляционной матрицы, поскольку заранее предполагается, что в наборе многомерных наблюдений скрыта простая структура, выражающаяся через дисперсии и ковариации переменных.
Метод главных компонент позволяет выявить группы элементов, наиболее тесно связанных с тем или иным мощным фактором. Элементы, однонаправлено изменяющие свое состояние под действием общего фактора, могут быть объединены в комбинации, называемые главными компонентами. Число последних намного меньше исходного числа параметров, в то же время они несут практически всю полезную информацию об изменчивости свойств, заключенную в исходной совокупности.
Главные компоненты вычисляются по формулам:
1ГК = ∑ωilxi = ω1l ·х1 + ω1х2 +.... +ωn1хn;
2ГК = ∑ωi2xi;
3ГК = ∑ωi3xi и т.д..
Здесь xi - значения параметров, ωij - факторные нагрузки (это влияние j -го фактора на i -й элемент, т.е. своего рода коэффициент корреляции между ними).
Таким образом, для нахождения главных компонент нам необходимо вычислить матрицу факторных нагрузок W. Она определяется из соотношения:
W = uΛ½
где u - матрица собственных векторов, а Λ - матрица собственных чисел корреляционной матрицы R. Элементы матрицы Λ определяются как корни характеристического уравнения:
|R-λ׀| = 0, где I - единичная матрица.
Вычислив этот определитель, получаем уравнение, степень которого и число полученных корней равны числу строк в корреляционной матрице R. При этом λ1 >λ2 >λ3... >λn, a ∑λi = n. Матрица u, находится из выражения:
(R - λ1)u=0
Подставляя в это уравнение найденные значения λi, получаем для каждого λi вектор значений ui. [7]
Таблица №7
| Матрица факторных нагрузок | ||
| Фактор 1 | Фактор 2 | |
| Na2O | -0,093441 | 0,478012 |
| MgO | -0,761341 | 0,454429 |
| Al2O3 | -0,095213 | 0,752748 |
| SiO2 | 0,935997 | -0,300714 |
| P2O5 | 0,543560 | 0,550328 |
| S* | 0,004238 | -0,761256 |
| K2O | 0,601771 | 0,479837 |
| CaO | -0,925268 | -0,117932 |
| TiO2 | -0,956019 | -0,005561 |
| MnO | 0,184793 | -0,023983 |
| Ti2O3 | -0,954002 | -0,178549 |
| ППП | -0,878921 | 0,137920 |
| Общ.дис. | 5,617994 | 2,270090 |
| Доля общ | 0,468166 | 0,189174 |
Как видим, 1-й фактор значимо влияет на все элементы. Такой фактор обычно называют генеральным. Генеральный фактор отрицательно сказывается на контрастности корреляционной матрицы, обуславливая перекрытие выделяемых групп. Дать главным факторам геологическую интерпретацию не всегда возможно, но когда это удается, информативность метода резко возрастает. В частности, в рассмотренном примере со 2-м фактором, видимо, связан процесс карбонатизации пород. Дать интерпретацию 1-му фактору сложнее. Возможно, это песчаники.
Метод главных компонент можно использовать и для распознавания образов. Для этого в координатах двух ГК выносятся значения для эталонных объектов и локализуются области, отвечающие этим объектам (рис. 7.)

Рисунок 7. Определение промышленного типа месторождения по методу главных компонентов.
а - 1-й промтип, б - 2-й промтип, в – непромышленнные объекты, г - изучаемое рудопроявление.
Таким образом МГК сводится к линейному преобразованию М исходных переменных в новых переменных, каждая из которых является линейной комбинацией исходных переменных. При этом МГК не является статистическим методом и мы практически не имеем формальных критериев для отбрасывания некоторых переменных или компонент, дающих очень малый вклад в суммарную дисперсию. О правильности своих действий мы можем судить только после проведения анализа МГК.
В отличие от МГК, факторный анализ считается статистическим методом, поскольку в его основе лежат некоторые предположения о природе изучаемой совокупности. Предполагается, что связь между m переменными является отражением корреляционной зависимости каждой из переменных с р взаимно некоррелированными факторами, причем р<m (если р = m, модель эквивалентна МГК). Поэтому дисперсию для m переменных можно вычислить с помощью дисперсии р – факторов плюс вклад, происхождение которого одинаково для всех переменных.
В Q-методе факторного анализа, в отличие от R-метода, анализируются взаимосвязи между наблюдениями, а не переменными.
Одно из главных препятствий в применении геологами различных модификаций факторного анализа заключено в абстрактности понятий собственных векторов и собственных значений корреляционных матриц. Между тем, эти категории имеют вполне определенный содержательный и геометрический смысл. На рис. 5 видно, что строки корреляционной матрицы можно представить как произвольные оси двумерного эллипсоида, тогда собственные вектора, дают направление главных осей эллипсоида, а корень из величины собственного значения – длину главных полуосей. Поскольку собственные значения включают в себя дисперсии переменных, очевидно, что и факторы отражают дисперсии (точнее, стандартные отклонения). При этом наклон и длина главных осей эллипсоида наглядно свидетельствуют о влиянии фактора на значения конкретной переменной.

Рисунок 8. Графическое изображение собственных векторов корреляционной матрицы.
Поскольку одна из главных задач факторного анализа - сокращение размерности исходного пространства признаков, важнейшим вопросом является выбор количества сохраненных факторов. Формального ответа на этот вопрос не существует, поэтому в большинстве случаев рекомендуется сохранять столько факторов, сколько имеется собственных чисел, больших 1, то есть сохраняются факторы, вклад которых в дисперсию больше, чем у каждой из исходных переменных. Эта рекомендация полезна в тех случаях, когда исходные данные хорошо скоррелированы и первые 2-3 фактора дают основной вклад в общую дисперсию. Если же переменные скоррелированы слабо, то половина и даже больше факторов может иметь собственные числа большие единицы. Число факторов получается слишком большим, причем вклад каждого из них в дисперсию невелик, а содержательная интерпретация затруднительна. В таких случаях применение факторной модели следует признать нецелесообразным.
В ряде случаев бывает затруднительно дать интерпретацию факторов даже если переменные хорошо скоррелированы. Перекрытие групп переменных зачастую обусловлено тем, что положение р ортогональных факторных осей в m-мерном пространстве определяется положением m–р ненужных ортогональных осей в выборочном пространстве. Исключив из рассмотрения ненужные оси, мы можем произвести вращение оставшихся факторных осей таким образом, чтобы выделенные группы наилучшим образом расположились в новых координатах. В наиболее часто используемом методе (метод варимакс Кайзера) вращение осуществляется до тех пор, пока проекции каждой переменной на факторные оси не окажутся близкими либо к нулю, либо к ±1. Чаще всего такое вращение приводит к тому, что для каждого фактора мы получаем несколько больших значений нагрузок и много близких к нулю. Это существенно облегчает содержательную интерпретацию факторов. Если же вращение факторных осей лишь ухудшает первоначальный результат, это свидетельствует либо о взаимной коррелированности факторов, либо о неприменимости выбранной факторной модели.
Графическое представление процедуры вращения факторных осей для двумерного случая дано на рис..

Рисунок 9. Вращение факторных осей для двумерного случая.
Проекции векторов переменных на факторные оси соответствуют их факторным нагрузкам. Видно, что после вращения разделение элементов на группы значительно улучшилось. При этом длина векторов и их относительное положение не изменились. [4]
Таким образом, факторный анализ сочетает в себе преимущества и возможности как методов группирования, так и распознавания образов. В частности, он может быть использован как вариант множественной регрессии для вычисления востановленных значений переменной:
Хвосст. = S⋅ωj⋅Z′j+х⋅ε΄,
где S – диагональная матрица m х m оценок стандартов m переменных;
ωj – факторная нагрузка j фактора;
Z´j – вектор-строка значений фактора j;
х - среднее значение параметра по выборочным данным;
ε΄ -вектор-строка размером N (число наблюдений) вида {1, 1, 1,.... 1}.
Таким способом можно оценить влияние каждого выделенного фактора (процесса) на распределение конкретного элемента и геометризовать в пространстве интенсивность этого влияния. Эта задача обычна при создании генетических моделей и прогнозо-поисковых комплексов. [10]
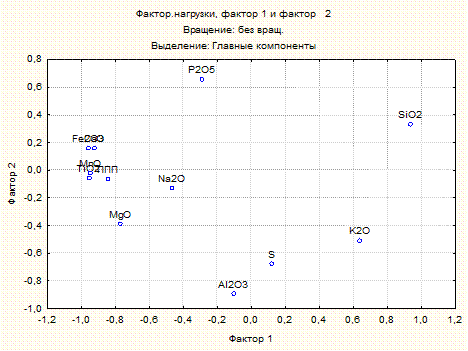
Рисунок 10. Фактор нагрузки
Заключение
Результаты контрольной работы помогли решить задачи достигнуть основную цель, которая дала понять и выяснить распределение полезных компонентов в пределах Черемховского участка, по данным полученным в результате опробования керна скважин и проведения рентгенофлуорисцентного анализа проб:
Было проведено 5 анализов:
1. Статистический анализ – анализ с помощью, которого были получены статистические характеристики для каждого компонента, которые образуют магматические горные породы (SiO2, S, TiO2, Al2O3, Fe2O3, MnO, MgO, CaO, Na2O, K2O, P2O5, ППП), представленные в таблице 2.
2. Корреляционный анализ – анализ, заключался в изучении коэффициентов корреляции между переменными, в результате, которого была создана таблица корреляции по всем элементам (таблица 4), где явно прослеживалась линейная взаимосвязь, на основании, которой были представлены диаграммы рассеяния (рисунок 3).
3. Регрессионный анализ – анализ, смысл которого, заключался в построении зависимостей между группами числовых переменных; в результате анализа была составлена таблица предсказанных значений и остатков, с зависимой переменной SiO2, на основании, которой был составлен нормальный вероятностный график остатков, который наглядно показывает отсутствие больших отклонений от высказанных предположений.
4. Кластерный анализ – ряд методов, который использовался для группировки объектов в кластеры на основе сходства их характерных признаков; в результате анализа «иерархическая классификация» была составлена дендрограмма горизонтальная, которая показывает степень близости кластеров, и последовательность их объединения и разделения, где в нашем случае наиболее дальше расположен элемент SiO2.
5. Факторный анализ – проведение анализа заключалось в выявлении влияния факторных нагрузок на элементы, в результате, чего была составлена таблица факторных нагрузок, и диаграмма факторных нагрузок, на котором явно прослеживается сосредотачивание группы элементов или их присутствие по отдельности.
В результате проведения всех анализов, можно предположительно сделать вывод о том, что результаты флуоресцентного анализа верны, выделено 2 кластера. Предположительно это силикаты, а точнее алюминиевый ряд гранатов.
В результате автор работы научился применять математические методы моделирования для обработки геологической информации, в программе «Statistica», которая является программным пакетом для статистического анализа, разработанного компанией StatSoft. Научился формулировать геологические задачи в пригодном виде для их решения. Научился применять наиболее эффективные методы. Также понял основные принципы геолого-математического моделирования.
Можно считать, что все поставленные задачи выполнены в полном объеме.
Список использованной литературы
1. Распознавание: [Электронный ресурс]. – URL: https://www.machinelearning.ru/ wiki/index.php?title=Эффективность. (Дата обращения 23.05.18).
2. Энатская Н. Ю., Хакимуллин Е. Р. «Математическая статистика. Учебное пособие» – Московский государственный институт электроники и математики. М., 2011. – 118с.
3. Гуськов, О.И. Математические методы в геологии. Сборник задач / О.И. Гуськов, П. И. Кушнарев, С.М. Таранов. – М.: Недра,2007. – 205 с.
4. Каждан, А.Б. Математические методы в геологии. Учебник для вузов / А.Б. Каж- дан, О.И. Гуськов, А.А. Шимановский. – М.: Недра, 2010. – 251 с.
5. Шестаков, Ю.С. Математические методы в геологии. Учебник для вузов. – Крас- ноярск: КИЦМ, 2008. – 208 с. б) дополнительная литература:
6. Беус, А.А. Руководство по предварительной математической обработке геохими- ческих данных при поисковых работах. М.: МГУ, 2006. – 118 с.
7. Ликеш И., Ляга Й. Основные таблицы математической статистики. - М.: Финансы и статистика, 1985. - 356 с.
8. Бериков В. С., Лбов Г. С. Современные тенденции в кластерном анализе // Всероссийский конкурсный отбор обзорно-аналитических статей по приоритетному направлению «Информационно-телекоммуникационные системы», 2008. — 26 с.
9. Вятченин Д. А. Нечёткие методы автоматической классификации. — Минск: Технопринт, 2004. — 219 с.
10. Дэвис Д. Статистический анализ данных в геологии. Книга 1. - М.: Недра, 1990. - 319 с.