Нормы расхода материалов

Задача 8.1.

Оптимизация местоположения склада методом центра тяжести.

Определите координаты оптимального местоположения складского комплекса и рассчитайте суммарные транспортные затраты на доставку продукции, опираясь на следующие исходные данные:

 

Вариант 9

№	Объект	Грузы, т/год	Тариф, руб/ткм	Коорд-ты
X	Y
	A
	B
	C
	D
	E

 

При решении задачи используйте метод центра тяжести. При ручных вычислениях с калькулятором выполните 2-3 итерации. При вычислениях в электронных таблицах Excel выполните 5-7 итераций.

Введем следующие условные обозначения:

Ÿ n – количество поставщиков и заказчиков;

Ÿ q_i – объем грузопотока i -го поставщика/заказчика, т/год;

Ÿ r_i – транспортный тариф i -го поставщика/заказчика, руб/ткм;

Ÿ x_i, y_i – координаты i -го поставщика/заказчика;

Ÿ x₀, y₀ – координаты складского комплекса;

Ÿ d_0i – расстояние между складским комплексом и i -м поставщиком/заказчиком.

Требуется определить оптимальные значения величин x₀, y₀, при которых будет выполняться следующее условие:

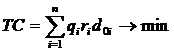(8.1)

где TC (Total Cost) – суммарные затраты на транспортировку, руб/год.

 

 

Нахождение оптимальных координат x₀, y₀ осуществляется с помощью итерационного сходящегося алгоритма. Количество итераций определяется требованиями к степени точности получаемого решения.

 

Алгоритм решения задачи методом центра тяжести:

Шаг 0.Начальный расчет величин x₀, y₀:

; .

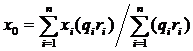На основании расчетов, приведенных в таблице 8.2, определяем начальные значения координат оптовой базы: x₀ = 512300/12800 = 40,02; y₀ = 729800/12800 = 57,02;

 

Таблица 8.2

 

№ п/п	Объект	xiqiri	yiqiri	qiri
	A
	B
	C
	D
	E
Сумма

 

Шаг 1. Расчет расстояний между складским комплексом и множеством поставщиков/заказчиков (см. табл. 8.3, графа 3):

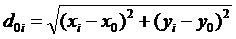
d₀₁ = =40,61

d₀₂= = 12,97

d₀₃= = 45,61

d₀₄= = 47,2

d₀₅= 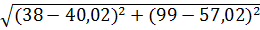= 42,03

Шаг 2. Расчет суммарных затрат на транспортировку (см. табл. 8.3, графа 4):

Шаг 3. Повторный расчет координат оптовой базы (см. табл. 8.3, графы 5-7):

; .

№ п/п	Объект	d0i	qirid0i	xiqiri/d0i	yiqiri/d0i	qiri/d0i
	A	40,61		5121,89	1969,95	78,8
	B	12,97		15612,95	23939,86	346,95
	C	45,61		175,4	3727,25	43,85
	D	47,2		779,66	440,68	33,9
	E	42,03		1356,17	3533,19	35,69
Сумма	-		23046,07	33610,93	539,19

 

В соответствии с проведенными вычислениями, определяем новые координаты оптовой базы: x₀ =23046,07/539,19=42,74; y₀ =33610,93/539,19=62,34. Отметим также, что при старых координатах оптовой базы (40,02;57,02) суммарные затраты на транспортировку, согласно табл. 8.3., составляют: TC = 418102 руб/год.

Шаг 4. Повторять шаги 1, 2 и 3 до тех пор, пока суммарные транспортные затраты TC не перестанут изменяться на значимую величину.

Новые координаты оптовой базы: x₀ = 42,74; y₀ = 62,34.

Повторим шаги 1, 2 и 3.

Шаг 1. Расчет расстояний между складским комплексом и множеством поставщиков/заказчиков (см. табл. 9.1, графа 3):

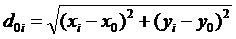
Произведем расчет с помощью программы Excel

Шаг 2. Расчет суммарных затрат на транспортировку (см. табл. 9.1, графа 4):

Шаг 3. Повторный расчет координат оптовой базы (см. табл. 9.1, графы 5-7):

; таблица.9.1.

№ п/п	Объект	d0i	qirid0i	xiqiri/d0i	yiqiri/d0i	qiri/d0i
	A	43,47	139109,12	4784,73	1840,28	73,61
	B	7,03	31648,55	28792,79	44148,95	639,84
	C	44,88		178,25	3787,83	44,56
	D	53,14	85027,68	692,48	391,40	30,10
	E	36,96	55447,8	1541,99	4017,29	40,57
Сумма	-	400994,14	35990,25	54185,76	828,7

 

В соответствии с проведенными вычислениями, определяем новые координаты оптовой базы: x₀ =43,43; y₀ =65,39. Отметим также, что при старых координатах оптовой базы (42,74; 62,34) суммарные затраты на транспортировку, согласно табл.9.1., составляют: TC = 400994,14 руб/год.

Сравним ТС₁ и ТС₂, числа 418102 и 400994,14. Разница этих величин значительна. Повторим шаги 1, 2 и 3 до тех пор, пока суммарные транспортные затраты TC не перестанут изменяться на значимую величину.

Новые координаты оптовой базы: x₀ =43,43; y₀ = 65,39.

Шаг 1. Расчет расстояний между складским комплексом и множеством поставщиков/заказчиков (см. табл. 9.2, графа 3):

Аналогично ведем расчеты при помощи Exсel.

Шаг 2. Расчет суммарных затрат на транспортировку (см. табл. 9.2, графа 4):

Шаг 3. Повторный расчет координат оптовой базы (см. табл. 9.2, графы 5-7):

; .

Таблица 9.2

№ п/п	Объект	d0i	qirid0i	xiqiri/d0i	yiqiri/d0i	qiri/d0i
	A	45,79		4542,477	1747,106	69,88425
	B	3,94		51395,94	78807,11	1142,132
	C	44,04		181,653	3860,127	45,41326
	D	56,23		654,4549	369,9093	28,45456
	E	34,05		1674,009	4361,233	44,05286
Сумма	-		58448,53	89145,48	1329,937

 

В соответствии с проведенными вычислениями, определяем новые координаты оптовой базы: x₀ =43,95; y₀ = 67,03.

Сравним ТС₂ и ТС₃, числа 400994 и 393381. Разница этих величин значительна. Повторим шаги 1, 2 и 3 до тех пор, пока суммарные транспортные затраты TC не перестанут изменяться на значимую величину.

Шаг 1. Расчет расстояний между складским комплексом и множеством поставщиков/заказчиков (см. табл. 9.3, графа 3):

Аналогично ведем расчеты при помощи Exсel.

Шаг 2. Расчет суммарных затрат на транспортировку (см. табл. 9.3, графа 4):

Шаг 3. Повторный расчет координат оптовой базы (см. табл. 9.3, графы 5-7):

; .

Таблица 9.3

№ п/п	Объект	d0i	qirid0i	xiqiri/d0i	yiqiri/d0i	qiri/d0i
	A	47,01		4424,591	1701,766	68,07062
	B	2,23		90807,17	139237,7	2017,937
	C	43,81		182,6067	3880,393	45,65168
	D	57,95		635,0302	358,9301	27,61001
	E	32,52		1752,768	4566,421	46,12546
Сумма	–		97802,17	149745,2	2205,395

 

В соответствии с проведенными вычислениями, определяем новые координаты оптовой базы: x₀ = 44,35; y₀ = 67,9

Сравним ТС₂ и ТС₃, числа 393381и 389587. Разница этих величин незначительна. Новые координаты оптовой базы: x₀ = 44,35; y₀ = 67,9.

С помощью калькулятора мы просчитали итерации. Определили координаты оптимального местоположения складского комплекса и рассчитали суммарные транспортные затраты на доставку продукции.

№ итерации	Координаты	TC, руб/год
X*	Y*
	42,74	62,34
	43,43	65,39
	43,95	67,03
	44,35	67,9
…	…	…	…

Склад будет иметь координаты (44,35;67,9). Суммарные затраты ТС=389587руб/год.

 

 

Задача 8.2.

Две производственные фирмы А и В, занимающиеся розливом минеральной воды, находятся на расстоянии S_AB км друг от друга. Производственные затраты фирм равны З_пр у.д.е. на единицу продукции.

Транспортировка продукции до потребителей осуществляется с помощью собственного парка автомобилей и транспортный тариф на перевозку одной единицы продукции составляет Т у.д.е./км (табл. 8.5).

Необходимо определить границы рынка для обеих фирм, если для расширения рынка сбыта своей продукции фирма Арешает использовать распределительный склад С, находящийся на расстоянии S_AC км от нее и на расстоянии S_CB км от фирмы-конкурента. Затраты, связанные с арендой складских помещений, составляют 3_склад у.д.е. на единицу продукции.

 

Таблица 8.5.

Номер варианта	SAB, км	Зпр, у.д.е./на ед. продукции	Т, у.д.е./км	SAC, км	SCB, км	3склад, у.д.е. за ед.
А	В	А	В
				0,9	0,8			1,4

 

Решение:

Продвигая свой товар на рынок сбыта, каждая фирма должна определить границы рынка, где она будет иметь преимущества. Если предположить, что качество товара разных производителей одинаково, то границы рынка будут напрямую зависеть от себестоимости продукции и затрат, связанных с доставкой товара к месту потребления, которые в сумме составляют продажную цену товара:

Ц = 3 + Т • х,

где Ц — цена реализации товара (без учета налогов и наценок), руб.;

3 — производственные затраты, руб.;

Т — транспортный тариф на перевозку груза, руб./км;

х — расстояние от продавца до потребителя товара, км.

Границей рынка будет точка безубыточности для фирм, т. е. территория, где цена реализации товара одной фирмы (произво­дитель А) будет равна цене другой фирмы (производитель В):

Ц _А = Ц _В,

или

3_A + T • x_A = 3_B + T • (d-x_A),

где d — расстояние между фирмами А и В.

В первую очередь определим границы рынка для фирм-производителей А и В в случае отсутствия склада С. Для этого составим и решим следующее уравнение:

Ц_А = Ц_В, т.е.

3_Апр + Т_А • х = 3_Впр + Т_в • (517-х)

14 у.д.е. + 0,9 у.д.е. * х = 16 у.д.е. + 0,8 у.д.е. * (517-х)

0,9х + 0,8х = 16 + 413,6 – 14

1,7х = 415,6

х = 244,5 (км.)

После введения в эксплуатацию склада С, уравнение примет следующий вид:

14 у.д.е. + 1,4 у.д.е. + 0,9 у.д.е. * х = 16 у.д.е. + 0,8 у.д.е. * (264-х)

0,9х + 0,8х = 16 + 211,2 – 15,4

1,7х = 211,8

х = 124,6 (км.)

Расчеты показали, что при использовании склада С границы рынка фирмы А расширятся и составят 377,5 км. (124,5 + 253). Границы рынка фирмы В расширятся и составят 508,5 км. (244,5 + 264).

 

Задача 8.3.

Компания ОАО «XYZ» планирует создание складского комплекса для хранения и сбыта продовольственных и промышленных товаров. Требуется рассчитать полезную и общую площадь склада, пропускную способность и месячный оборот склада, средний срок хранения груза.

Показатель		Вариант
Расчетная емкость склада, т	Е
Использование емкости склада	g	0,60
Плановый грузооборот, т/год	Q
Количество раб. дней в году	D
Средняя плотность груза, т/м3	r	0,45
Высота укладки, м	H
Плотность укладки	b	0,64
Использование площади склада	α	0,50

 

Показатель	Алгоритм расчета
Полезная площадь склада, м2	Sпол = E / (H ´ r ´ b)
Общая площадь склада, м2	Sобщ = Sпол / a
Средний срок хранения груза, дней	tср = Dp ´ g ´ E / Q
Пропускная способность склада, т	F = Е / tср
Месячный оборот склада	По = Dp / tср

 

Решение:

1. Полезная площадь склада

S_пол = 4500/4*0,45*0,64 = 3906,25 м² .

2. Общая площадь склада

S_общ = 3906,25/0,50 = 7812,5 м².

3. Средний срок хранения груза

t_ср = 250*0,60*4500/90000 = 8 дней.

4. Пропускная способность склада

F= 4500/8 = 562,5 т.

5. Месячный оборот склада

П_о = 30/8 = 3,75.

 

 

Задача 8.5.

Определить величину оборотного и страхового запасов материалов и необходимую общую площадь склада. Нормы расхода материалов приведены в табл. 8.9.

Сроки поставки материалов:

· сталь сортовая конструкционная – 1 раз в месяц;

· сталь сортовая легированная – 2 раза в квартал;

· сталь листовая – 1 раз в месяц;

· латунные трубки – 1 раз в квартал.

Остальные исходные данные по вариантам сведены в табл. 8.10 и 8.11.

Таблица 8.9

Нормы расхода материалов

 

Материал	Нормы расхода по изделиям, кг/шт.
А	Б	В	Г
Сталь сортовая конструкционная
Сталь сортовая легированная
Сталь листовая	-
Латунные трубы			-

 

Таблица 8.10

Квартальнаяпрограмма выпуска изделия, шт.

Изделия	Вариант 9
А
Б
В
Г

 

Таблица 8.11

Исходные данные

Показатель	Вариант 9
Время доставки материалов от поставщиков, дн	Сталь
латунные трубки
Допустимая нагрузка, т/м2	сталь сортовая
сталь листовая	3,4
латунные трубки	1,7
Коэффициент использования грузовой площади склада	0,7

Решение:

Квартальная потребность по видам материалов (M_i) определяется по формуле:

,

где N_j – квартальнаяпрограмма выпуска j -го изделия, шт.;

– норма расхода i -го материала на j -е изделия, кг.

М₁= 1000*30 + 350*100 + 200*300 + 100*50 = 130000

М₂= 1000*80 + 350*60 + 200*30 + 100*15 = 108500

М₃= 350*500 + 200*750 + 100*60 = 331000

М₄= 1000*25 + 350*30 + 100*20 = 37500

Среднесуточная потребность (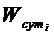) по видам материалов

W_сут1 = (130000/1000)/90 = 1,44

W_сут2 = (108500/1000)/90 = 1,21

W_сут3 = (331000/1000)/90 = 3,67

W_сут4 = (37500/1000)/90 = 0,42

Максимальный текущий запас ():

,

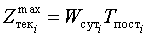где – период между двумя очередными поставками i -го материала, дн.

= 1,44 * 30 = 43,2

= 1,21 * 45 = 54,45

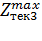= 3,67 * 30 = 110,1

= 0,42 * 90 = 37,8

Страховой запас ()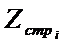

,

где – время суточного восстановления запаса i -го материала (включая время на оформление срочной поставки, погрузку, транспортировку, разгрузку).

Z_стр1 = 1,44 * 9 = 12,96

Z_стр2 = 1,21 * 9 = 10,89

Z_стр3= 3,67 * 9 = 33,03

Z_стр4= 0,42 * 8 = 3,36

Максимальный производственный запас

= 43,2 + 12,96 = 56,16

= 54,45 + 10,89 = 65,34

= 110,1 + 33,03 = 143,13

= 37,8 + 3,36 = 41,16

Общая площадь склада (S_общ)

,

где i =1, …, m – количество видов материалов;

q_i – допустимая нагрузка на 1 м² склада по виду материала, т;

k – коэффициент использования грузовой площади склада

S_общ. = 56,16/(1*0,7) + 143,13/(3,4*0,7) + 41,16/(1,7*0,7) = 174,96 м².

 

Задача 8.6.

На основе данных, представленных в табл. 8.12, необходимо рассчитать совокупный материальный поток на складе.

Обозначения в таблице:

входной материальный поток — Q;

доля товаров, поставляемых в нерабочее время, — d₁;

доля товаров, подлежащих распаковке на участке приемки, — d₂;

доля товаров, подлежащих комплектованию, — d₃;

доля товаров, поставляемых централизованно, — d₄;

доля доставленных товаров, подлежащих ручной разгрузке, — d₅;

доля товаров, подлежащих ручной погрузке, — d₆;

кратность обработки товаров на участке хранения — d₇.

Таблица 8.12

Номер варианта	Q	d1	d2	d3	d4	d 5	d6	d7

Решение:

Грузопоток — показатель, характеризующий процесс перемещения грузов на определенном участке работы склада. Его величина определяется количеством груза, перемещенного по данному участку в единицу времени (час, смену, сутки, месяц, квартал, год).

Совокупный МП определяется по формуле

Р = Р_РР + Р_МР + Р_РП + Р_МП +Р_Э + Р_ПК +Р_Х+ Р_ПГ,

где Р — совокупный материальный поток;

Р_РР, Р_мр — материальный поток при ручной и механической разгрузке соответственно;

 

P_РП, Р_МП — материальный поток при ручной и механической погрузке соответственно;

Р_Э — материальный поток на экспедиционных участках;

Р_ПК — материальный поток на участках приемки и комплектации;

Р_Х — материальный поток в зоне хранения;

Р_ПГ — внутрискладское перемещение грузов.

Грузопоток при ручной разгрузке определяется по следующей формуле:

P_PP = Q × d₅: 100,

где Q - входной поток (грузооборот склада), т/год.

Рассчитаем грузопоток при ручной разгрузке:

P_PP = 2510*32/100 = 803,2

Грузопоток при механической разгрузке определяется по формуле

P_MP = Q (1 - d₅ /100).

Рассчитаем грузопоток при механической разгрузке:

P_MP = 2510*(1 – 32/100) = 1706,8

Аналогично определяется грузопоток при ручной и механи­ческой погрузке.

Рассчитаем грузопоток при ручной и механи­ческой погрузке соответственно:

P_РП =Q * d₆ / 100

P_РП = 2510*64/100 = 1606,4

Р_МП =Q* (1 – d₆ /100)

Р_МП = 2510*(1 – 64/100) = 903,6

Материальный поток на экспедиционных участках рассчиты­вается по формуле

P_Э = Q (d₁ + d₄): 100.

Рассчитаем материальный поток на экспедиционных участках:

P_Э = 2510*(13+50)/100 = 1581,3

Подобным образом определяется материальный поток на участках приемки и комплектации:

P_ПK = Q (d₂ + d₃): 100.

Определим материальный поток на участках приемки и комплектации:

P_ПK = 2510*(26 + 46)/100 = 1807,2

В зоне хранения в результате множества таких операций, как, например, перекладывание товара с одного яруса на другой или отбор товара, возникает группа материальных потоков, сумма ко­торых может быть представлена как величина, кратная грузообо­роту склада:

P_Х = Q × d₇.

P_Х = 2510*2 = 5020

Внутрискладское перемещение грузов равно сумме выходных грузовых потоков всех участков, кроме последнего:

Р_ПГ = Q _{разгрузка} + Q × d₁: 100+ Q × d₂: 100 + Q_{хранение} +

+ Q × d₃: 100 + Q × d₄: 100.

Р_ПГ =

2510 + 2510*13/100 + 2510*26/100 + 2510 + 2510*46/100 + 2510*50/100 =

= 2510 + 326,3 + 652,6 + 2510 + 1154,6 + 1255 = 8408,5

Совокупный МП определяется по формуле:

Р = Р_РР + Р_МР + Р_РП + Р_МП +Р_Э + Р_ПК +Р_Х+ Р_ПГ

Р = 803,5 + 1706,8 + 1606,4 + 903,6 + 1581,3 + 1807,2 + 5020 + 8408,5 = 21837,3 ед. груза/ ед.времени.

 

 

Задача 8.7.

На склад для разгрузки поступает простейший поток грузовиков с интенсивностью λ = 3 грузовика/ч. Разгрузка одного грузовика занимает t_обсл = 15 мин = 0,25 ч. Найти параметры этой одноканальной СМО с фиксированным временем обслуживания.

Решение:

λ = 3 грузовика/ч.

t_обсл = 15 мин = 0,25 ч.

μ = 1/ t_обсл = 1/0,25 = 4 грузовика/ч.

Средняя длина очереди L_оч = 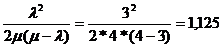грузовика.

Среднее время ожидания в очереди Т_оч = L_оч / λ = 1,125/3 = 0,375 ч = 0,375×60 = 22,5 мин.

Вывод: в результате практической работы, мы научились решать задачи логистики складирования.

 

Список литературы:

1. Неруш Ю.М., Неруш А.Ю. Практикум по логистике: Учебное пособие. – М.: ТК Велби, изд-во Проспект, 2008. С.74-114.

2. Гаджинский А.М. Современный склад. Организация, технологии, управление и логистика: Учебно-практическое пособие. М.: Проспект, ТК Велби, 2007. 176 с.

3. Черкесов А.Г. Экономическая теория. Математические модели: Учеб. пособие. СПб.: Изд-во СПбГПУ, 2003. 52 с.