МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ФИЗИЧЕСКИЙ ФАКУЛЬТЕТ
Кафедра лазерной физики и спектроскопии
РАЗГРУЗКА РЕЗОНАТОРА ПОСРЕДСТВОМ ГЕНЕРАЦИИ ВТОРОЙ ГАРМОНИКИ
Курсовая работа
Новицкой Розы Игоревны
студентки 3 курса, специальности
физика (научно-исследовательская
деятельность)
Научный руководитель:
кандидат физико-математических наук
доцент Сташкевич И. В.
 Минск, 2016
Минск, 2016
Содержание
Введение....................................................................................................... 2
1 Метод разгрузки резонатора с помощью генерации второй гармоники 3
1.1 Теоретико-методологический обзор................................................. 3
1.2 Описание метода................................................................................. 4
1.3 Схема установки................................................................................. 4
2 Построение модели.................................................................................. 6
2.1 Характеристики лазера...................................................................... 6
2.2 Точечная модель активной среды..................................................... 7
2.3 Балансные уравнения......................................................................... 7
2.4 Метод расчета..................................................................................... 9
3 Режим генерации основной частоты...................................................... 10
3.1 Особенности моделирования........................................................... 10
3.2 Генерация с переходом в стационарное состояние......................... 10
4 Режим генерации второй гармоники..................................................... 12
4.1 Особенности моделирования........................................................... 12
4.2 Расчет формы выходного импульса................................................ 13
5 Анализ полученных результатов.......................................................... 15
5.1 Зависимость длительности импульса от мощности накачки.......... 15
5.2 Зависимость длительности импульса от коэффициента потерь..... 15
Заключение................................................................................................ 17
Список использованных источников........................................................ 18
Введение
В настоящее время основным методом получения коротких импульсов лазерного излучения большой мощности является генерация гигантского импульса. В этом случае накачка производится до тех пор, пока инверсия населенностей не достигнет максимального значения. Тогда включается добротность резонатора, и число фотонов в нем начинает быстро увеличиваться, что приводит к возникновению короткого интенсивного импульса. В данном методе важно значение времени жизни частиц на верхнем уровне, которое должно быть достаточно большим.
Одним из альтернативных методов является разгрузка резонатора посредством формирования импульсов излучения второй гармоники. Его основным преимуществом является гораздо более качественное лазерное излучение на выходе и независимость от времени жизни на уровнях. В данном случае энергия импульса запасается в резонаторе в виде излучения и выводится только после достижения системой стационарного режима генерации. Такой метод может быть использован для создания коротких импульсов высококогерентного лазерного излучения в видимом диапазоне длин волн.
При использовании данного метода разгрузки резонатора необходимо учитывать, что интенсивность излучения в резонаторе достигает достаточно большой величины. Её максимальное значение ограничивается величиной световой прочности элементов установки, при которой система еще способна исправно функционировать.
Курсовая работа посвящена теоретическому моделированию и анализу метода разгрузки резонатора с помощью генерации второй гармоники и расчетам основных характеристик выходного импульса. Также рассмотрено влияние мощности накачки и коэффициента потерь на длительность импульса.
1 Метод разгрузки резонатора с помощью генерации второй гармоники
1.1 Теоретико-методологический обзор
Техника разгрузки резонатора позволяет вывести энергию, накопленную в лазере, за время, равное времени полного прохода резонатора. Для этого могут быть использованы различные методы и установки [1]. Один из основных методов заключается в выведении пучка из лазера с глухими зеркалами с помощью устройства с переменным коэффициентом отражения (рисунок 1.1). До определенного времени он равен нулю, а когда интенсивность излучения в резонаторе становится максимальной, резко возрастает до значения, близкого к 100%. Часто для этого используются электрооптические модуляторы на ячейках Поккельса или акустооптические ячейки. Такие устройства позволяют разгрузить резонатор за два прохода.

Рисунок 1.1 – Принцип работы лазера с разгрузкой резонатора.
Разгрузка резонатора является общим методом, применяемом в лазерах с синхронизацией мод, непрерывных лазерах и лазерах с модуляцией добротности. Особый интерес представляет случай лазеров с синхронизацией мод. При этом разгрузку проводят в тот момент времени, когда внутрирезонаторный импульс достигает максимума, и на выходе резонатора формируется единственный мощный импульс длительностью порядка 10-12 – 10-14 секунд.
1.2 Описание метода
Рассмотренный метод разгрузки резонатора позволяет получить короткие импульсы лазерного излучения в видимом диапазоне длин волн. Для этого используется преобразование излучения неодимового лазера во вторую гармонику и дальнейшее выведение его из резонатора в виде импульсов определенной длительности и интенсивности. Высокая когерентность и качественность излучения обеспечиваются тем, что перед формированием импульса система достигает стационарного режима генерации, необходимого для стабилизации пространственного распределения излучения в резонаторе и оптимизации параметров пучка.
Управление генерацией второй гармоники осуществляется с помощью электрооптического кристалла, работающего по принципу ячейки Поккельса.
1.3 Схема установки
На рисунке 1.2 приведена схема установки для разгрузки резонатора.
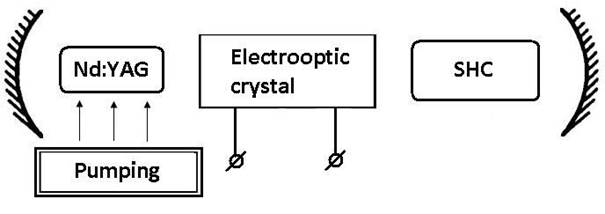
Рисунок 1.2 – Схема установки.
Резонатор ограничен двумя сферическими зеркалами и включает в себя три основных элемента: лазерный элемент, электрооптический кристалл и кристалл второй гармоники.
Лазерный элемент представляет собой кристалл иттрий-алюминиевого граната (ИАГ, или YAG - yttrium aluminum garnet)Y3Al5O12, легированного ионами неодима Nd (концентрация ионов 1%). Лазер работает по стандартной четырехуровневой схеме и генерирует излучение на длине волны 1064 нм.
Преобразование излучения во вторую гармонику возможно в анизотропном кристалле второй гармоники (KTP/DKDP) при выполнении условий фазового синхронизма (например, равенство показателей преломления необыкновенной волны на удвоенной частоте и обыкновенной волны на основной частоте). Для этого кристалл располагается под определенным углом к направлению падения излучения.
Электрооптический кристалл является управляющим элементом, при подаче напряжения на него начинается генерация второй гармоники. Так, если напряжение равно нулю, проходящее излучение сохраняет линейную поляризацию и условия фазового синхронизма в кристалле второй гармоники не выполняются. Определенный уровень напряжения создает разность показателей преломления обыкновенной и необыкновенной волн, соответствующую круговой поляризации излучения. При этом выполняются условия фазового синхронизма, и генерация второй гармоники становится возможной.
Рассмотренная схема имеет два последовательных режима работы: генерация излучения основной частоты (сосредоточенного внутри резонатора) с переходом в стационарный режим и формирование импульсов излучения второй гармоники. Переключение между этими двумя режимами и осуществляется с помощью изменения напряжения на электрооптическом кристалле.
2 Построение модели
2.1. Характеристики лазера
В качестве лазерного элемента в работе рассматривается кристалл Nd:YAG с торцевой накачкой полупроводниковым диодом, работающий по четырехуровневой схеме. На рисунке 2 представлена схема уровней и переходов, соответствующая такому режиму генерации.

Рисунок 2 – Схема переходов и уровней энергии Nd:YAG; длины волн указаны в нм, энергии в см-1.
Генерация происходит на длине волны 1064 нм при вынужденных переходах с уровня 4F3/2 на уровень 4I11/2 (расщепление уровней не учитывается). Возбуждение ионов активной среды из основного состояния осуществляется с помощью торцевой накачки полупроводниковым диодом на длине волны 808 нм. Время жизни ионов на уровне 4F5/2 составляет порядка 10 нс, переходы с него на нижележащий метастабильный уровень 4F3/2 являются безизлучательными. Такие переходы также происходят с уровня 4I11/2 (время жизни – 30 нс) в основное состояние 4I9/2.
Основные параметры системы приведены в таблице 1 [2].
Таблица 1 – Значения длины волн накачки и генерации, сечений поглощения и излучения, времени жизни на уровне 4F3/2 и показателя преломления лазерного кристалла Nd:YAG.
| Кристалл | длина волны накачки λ0, нм | длина волны генерации λ, нм | Сечение поглощения σа, 10-20 см2 | Сечение излучения σе, 10-20 см2 | Время жизни на уровне 4F3/2 τ2, мс | Показатель преломления n |
| Nd:YAG | 7.7 | 1.82 |
Характеристики резонатора и активной среды: длина активного элемента Lar = 4 см, длина прокачиваемой области lar = 1 см, длина резонатора Lc = 20 cм, диаметр области, на которую фокусируется излучение накачки da = 0.03 cм.
2.2 Точечная модель активной среды
В рамках рассматриваемой задачи применимо приближение точечной модели активной среды. При этом предполагается, что время поперечной релаксации системы мало по сравнению со временем продольной релаксации и временем жизни фотона в резонаторе, что выполняется для твердотельных лазеров (в том числе и неодимового). Такая модель может быть использована для описания однородных сред и предполагает, что все пространство активной среды сведено в одну точку. Таким образом, пространственное изменение параметров системы, таких как населенности уровней и плотность потока фотонов в резонаторе, не рассматривается, учитывается только их временная зависимость.
Точечная модель активной среды позволяет применять балансные (скоростные) уравнения типа Статца-Де Марса для описания динамики генерации [3].
2.3 Балансные уравнения
Процесс генерации неодимового лазера по четырехуровневой схеме описывается балансными уравнениями (2.1). Решая данную систему уравнений, можно получить зависимости населенностей на уровнях и плотности потока фотонов в резонаторе от времени.
 (2.1)
(2.1)
Здесь ni и τi, где i =1,2,3, – плотности населенности [см-3] и времена жизни [мкс] нижнего лазерного уровня (4I11/2), уровней 4F3/2 и 4F5/2 соответственно. Объемная плотность ионов неодима в кристалле при концентрации 1% равна Ns = 1.38·1020 см-3. Слагаемые вида ni /τi описывают изменение населенности частиц на уровнях за счет спонтанных переходов. Вероятности спонтанных переходов с поглощением и испусканием считаются равными, поэтому они не вносят вклада в изменение плотности потока фотонов в резонаторе.
S – плотность потока фотонов в резонаторе, R0 – плотность потока фотонов накачки [фотон·см-2∙мкс-1]. Она определяется мощностью накачки P [Вт] и рассчитывается по формуле
 , (2.2)
, (2.2)
где sar – площадь области активной среды, на которую фокусируется излучение накачки.
Сечения излучения σе и поглощения σа [10-20 см2] описывают вероятности соответствующих процессов в системе.
Величина μ характеризует степень заполнения резонатора активной средой; rtc - величина, обратная времени жизни фотона в резонаторе [мкс-1]; vc – скорость света в среде [см/мкс]. Величины μ и rtc рассчитываются по формулам (2.3) и (2.4) соответственно.
 (2.3)
(2.3)
 (2.4)
(2.4)
Здесь ρ – коэффициент отражения одного из выходных зеркал (другого – 100%); γ – коэффициент неактивных потерь в резонаторе, описывает всевозможные потери, не связанные с выходом излучения через зеркала (например, рассеяние и поглощение элементами внутри резонатора) и равен 0.003 для стандартного неодимового лазера.
Таким образом, коэффициент vcμ определяет вклад в усиление плотности потока фотонов при прохождении излучения внутри активного вещества, а слагаемое Srtc описывает потери излучения в резонаторе, обусловленные его выходом через полупрозрачное зеркало.
2.4 Метод расчета
Решение нелинейной системы дифференциальных уравнений (2.1) находилось явным методом Рунге-Кутта четвертого порядка с адаптацией шага. Для этого в программе Mathcad использовался оператор Rkadapt (x, 0, t, N, D).
Здесь x – матрица искомых величин в начальный момент времени, x = (10-10, 0, 0, 0). Тепловой заселенностью уровней пренебрегаем, т.к. она несущественна в рассматриваемой задаче (менее 1% для нижнего из уровней 4I11/2). Второй и третий аргументы – начальный и конечный момент времени соответственно. N – количество точек решения дифференциальных уравнений. D – векторная функция, определяющая правую часть системы (2.1).
В соответствии с двумя режимами работы системы моделирование проводится в два этапа, каждому из которых соответствует определенные значения характеристик системы. Параметры t и NN также различны и зависят от масштаба по времени и динамики генерации на данном этапе.
3 Режим генерации основной частоты
3.1 Особенности моделирования
Режим генерации основной частоты с переходом в стационарный режим является необходимым этапом перед формированием импульсов излучения второй гармоники. Стационарный режим генерации соответствует установившемуся во времени и пространстве излучению внутри резонатора.
На данном этапе напряжение на электрооптическом кристалле равно нулю и генерации второй гармоники не происходит. Все излучение основной частоты должно быть заключено внутри резонатора, для чего подбираются выходные зеркала с коэффициентом отражения ρ≈1 на длине волны 1064 нм. Накачка производится непрерывно с постоянной мощностью, которая определяет интенсивность излучения в резонаторе. Расчет проводился с плотностью узлов 100 точек на мкс.
3.2 Генерация с переходом в стационарное состояние
Решением системы уравнений является зависимость плотности потока фотонов основной частоты S1 в резонаторе от времени. Данная зависимость для мощности накачки P = 2 Вт представлена на рисунке 3.1.

Рисунок 3.1 – Зависимость плотности потока фотонов в резонаторе от времени, мощность накачки 2 Вт.
Интенсивность генерации при постоянном возбуждении имеет пичковую структуру с выходом на стационарное значение. Из графика видно, что для достижения стационарного режима при данных условиях системе потребовалось около 5 мкс. Как показано на рисунке 3.2, это время зависит от мощности накачки.

Рисунок 3.2 – Зависимость времени, необходимого для перехода в стационарный режим генерации, от мощности накачки.
С ростом мощности накачки величина времени убывает монотонно и в среднем составляет около 4-5 мкс.
Таким образом, этап генерации основной частоты заключается в формировании устойчивого распределения излучения внутри резонатора и занимает порядка нескольких микросекунд. После этого можно переходить к генерации импульсов излучения второй гармоники.
Режим генерации второй гармоники
4.1 Особенности моделирования
Для перехода в этот режим необходимо подать определенное напряжение на электрооптический кристалл. При этом часть энергии излучения основной частоты будет преобразовываться во вторую гармонику. При моделировании считалось, что интенсивность излучения второй гармоники пропорциональна квадрату интенсивности первой. Такое приближение неприменимо при значительных интенсивностях (соответственно, и мощностях накачки), тогда зависимость становится более сложной. В расчетах использовались мощности меньшие 10 Вт, при которых условие квадратичной зависимости выполняется. Коэффициент пропорциональности определялся из условия, что при интенсивности излучения внутри резонатора I1 = 1МВт·см-2 1% энергии преобразуется во вторую гармонику.
Для эффективного формирования выходного импульса одно из зеркал резонатора необходимо сделать практически полностью прозрачным для излучения второй гармоники, а второе – полностью отражающим. Часть энергии излучения выводится из резонатора в виде импульсов второй гармоники, поэтому интенсивность излучения основной частоты внутри резонатора будет уменьшаться. Этот эффект при моделировании учитывался во введении зависимости коэффициента отражения одного из выходных зеркал от плотности потока фотонов первой гармоники (4.1).
 (4.1)
(4.1)
Т.е., чем больше плотность потока фотонов в резонаторе, тем больше коэффициент преобразования во вторую гармонику и тем сильнее уменьшается интенсивность излучения основной частоты.
Начальные значения параметров системы (S1 и ni) на данном этапе принимались равными их значениям в стационарном режиме генерации на предыдущем этапе.
Расчет проводился с плотностью узлов 1000 точек на мкс.
4.2 Расчет формы выходного импульса
Для нахождения зависимости интенсивности излучения основной частоты внутри резонатора от времени решалась система уравнений вида (2.1) с учетом вышеприведенных особенностей, после чего по формуле (4.2) определялась интенсивность выходного импульса.
 (4.2)
(4.2)
Зависимость интенсивности импульса излучения второй гармоники I2 от времени представлена на рисунке 4.1.

Рисунок 4.1 – Зависимость интенсивности выходного импульса от времени, мощность накачки 6 Вт.
Полученный импульс имеет ступенчатую структуру в начале, т.к. время переключения электрооптического затвора считалось бесконечно малым (в реальных устройствах оно составляет порядка 1 нс).
В данном случае системе потребовалось около 2 мкс для перехода в стационарный режим. Длительность полученного импульса соответствует его полуширине и составляет примерно 12 нс, что гораздо меньше этого времени.
Длительность импульса, как и его интенсивность, зависит от мощности накачки. На рисунке 4.2 показана форма генерируемых при разных мощностях накачки импульсов.

Рисунок 4.2 – Зависимости интенсивности выходного импульса от времени для мощностей накачки 2, 4 и 6 Вт.
С увеличением мощности импульс становится более интенсивным и коротким. Исследование зависимости длительности импульса от мощности накачки проводится в следующей главе.