Задача 13. Могут ли следующие уравнения быть преобразованы в уравнения, линейные по параметрам?
а) 
б) 
в) 
г) 
Решение. Уравнения б) и г) не могут быть преобразованы в уравнения линейные по параметрам, т.е. они нелинейные по параметрам
А а) и в) могут, если прологарифмировать обе части уравнения.
а) 
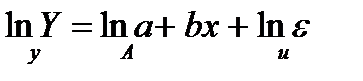
 - уравнение линейное по параметрам
- уравнение линейное по параметрам
в) 
 - уравнение линейное по параметрам
- уравнение линейное по параметрам
Решение типовых задач:
Пример 1
По семи территориям Уральского района за 200Х г. известны значения двух признаков (табл. 1.1).
Таблица 1.1
| Номер региона | Расходы на покупку продовольственных товаров в общих расходах, %, у | Среднедневная заработная плата одного работающего, тыс. руб., х |
| 68,8 | 4,5 | |
| 58,3 | 5,9 | |
| 62,6 | 5,7 | |
| 52,1 | 7,2 | |
| 54,5 | 6,2 | |
| 57,1 | 6,0 | |
| 51,0 | 7,8 |
Требуется: 1. Для характеристики зависимости у от х рассчитать параметры следующих функций:
а) линейной; б) степенной; в) показательной; г) полулогарифмической; д) обратной; е) равносторонней гиперболы.
2. Найти показатели тесноты связи по каждой модели.
3. Оценить каждую модель через показатель детерминации, среднюю ошибку аппроксимации  ,
,  - критерий Фишера и выбрать наилучшую из них.
- критерий Фишера и выбрать наилучшую из них.
Решение: 1а. Для расчета параметров а и b линейной регрессии 
решаем систему нормальных уравнений относительно:  и
и  :
:

По исходным данным рассчитываем  ,
, 



Таблица 1.2 
| у | х | ух | х2 | у2 | 
| 
| Аi | |
| 68,8 | 4,5 | 309,6 | 20,25 | 4733,44 | 67,1 | 1,7 | 2,47 | |
| 58,3 | 5,9 | 343,97 | 34,81 | 3398, 89 | 59,3 | -1,0 | 1,72 | |
| 62.6 | 5,7 | 356, 82 | 32,49 | 3918,76 | 60,4 | 2,2 | 0,51 | |
| 56,7 | 7,2 | 375,12 | 51,84 | 2714,41 | 52,2 | -0,1 | 0,19 | |
| 55,0 | 6,2 | 337,9 | 38,44 | 2970,25 | 57,7 | -3.2 | 5,87 | |
| 54,3 | 342,6 | 3260,41 | 58,8 | -1,7 | 2,98 | |||
| 7,8 | 397,8 | 60,84 | 2601,00 | 48,9 | 2,1 | 4,12 | ||
| Итого | 404,4 | 43,3 | 2463,81 | 274,67 | 23597,16 | 404,4 | 0,0 | 20,86 |
| Среднее значение | 57,77 | 6,186 | 351,97 | 39,24 | 3371,02 | - | - | 3,48 |

| 5,80 | 0,9676 | ||||||

| 33,65 | 0,9363 |
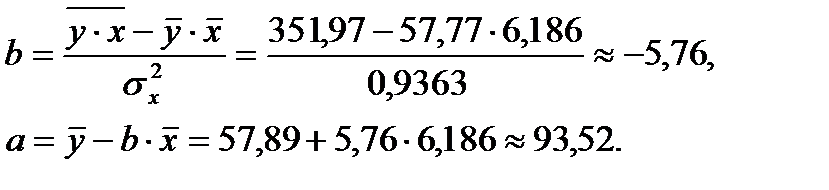
Уравнение регрессии:  С увеличением среднедневной заработной платы на 1 руб. доля расходов на покупку продовольственных товаров снижается в среднем на 0,35 процентных пункта.
С увеличением среднедневной заработной платы на 1 руб. доля расходов на покупку продовольственных товаров снижается в среднем на 0,35 процентных пункта.
Рассчитаем линейный коэффициент парной корреляции:

Связь умеренная, обратная.
Определим коэффициент детерминации:

Вариация результата на 7,7% объясняется вариацией факторах х. Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчетные) значения ух. Найдем величину средней ошибки аппроксимации  :
:

Точность модели высокая, в среднем расчетные значения отклоняются от фактических на 2,98 %.
Рассчитаем F-критерий:
 . Табличное значение F-критерия при числе степеней свободы 1 и 5 и уровне значимости 0,05 составит Fт =6,61. Т.е. фактическое значение больше табличного, это указывает на статистическую значимость уравнения регрессии.
. Табличное значение F-критерия при числе степеней свободы 1 и 5 и уровне значимости 0,05 составит Fт =6,61. Т.е. фактическое значение больше табличного, это указывает на статистическую значимость уравнения регрессии.
1б. Построению степенной модели  предшествует процедура линеаризации переменных. В примере линеаризация производится путем логарифмирования обеих частей уравнения:
предшествует процедура линеаризации переменных. В примере линеаризация производится путем логарифмирования обеих частей уравнения:
 где
где  Для расчетов используем данные табл. 1.3. Рассчитаем С и b:
Для расчетов используем данные табл. 1.3. Рассчитаем С и b:

Получим линейное уравнение: 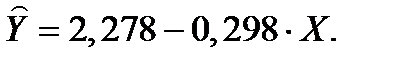
Выполнив его потенцирование, получим:

Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата  . По ним рассчитаем показатели: тесноты связи - индекс корреляции рху и среднюю ошибку аппроксимации
. По ним рассчитаем показатели: тесноты связи - индекс корреляции рху и среднюю ошибку аппроксимации  :
:


Характеристики степенной модели указывают, что она несколько лучше линейной функции описывает взаимосвязь.
Таблица 1.3
| Y | X | YX | Y2 | X2 | 
| 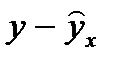
| 
| 
| |
| 4,2316 | 1, 5042 | 6, 364 | 17,901 | 4,228 | 68,6 | 0,2 | 0,04 | 0,29 | |
| 4,0660 | 1,7754 | 7,2174 | 16,532 | 4,071 | 58,6 | -0,3 | 0,09 | 0,52 | |
| 4,1374 | 1,7404 | 7.198 | 17,115 | 4,092 | 59,9 | 2,7 | 7,29 | 4,31 | |
| 3,9532 | 1,9741 | 7,803 | 15,626 | 3,957 | 52,3 | -0,2 | 0,04 | 0,39 | |
| 3,948 | 1,8252 | 7,296 | 15,984 | 4,042 | 56,9 | -2,4 | 5,76 | 4,4 | |
| 4,0452 | 1, 7926 | 8,076 | 16,362 | 4,062 | 58,1 | -1,0 | 1,0 | 1,75 | |
| 3, 932 | 2,0543 | 2,9487 | 15,461 | 3,910 | 49,9 | 1,1 | 1,21 | 2.16 | |
| Итого | 28,362 | 12,664 | 51,203 | 114,981 | 23,098 | 404,3 | 0,1 | 15,43 | 13,79 |
| Среднее значениее | 4, 052 | 1,8090 | 7,315 | 16,426 | 3,30 | 1,97 | |||

| 0,0854 | 0,1659 | |||||||

| 0,0073 | 0,0275 |
1в. Построению уравнения показательной кривой 
предшествует процедура линеаризации переменных при логарифмировании обеих частей уравнения:

где 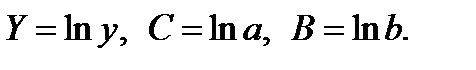
Для расчетов используем данные табл. 1.4.Значения параметров регрессии А и В составили:

Получено линейное уравнение: 
Произведем потенцирование полученного уравнения и запишем его в обычной форме:
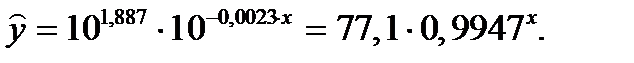
Тесноту связи оценим через индекс корреляции  :
:
 Связь умеренная.
Связь умеренная.  , что говорит о повышенной ошибке аппроксимации, но в допустимых пределах. Показательная функция чуть хуже, чем степенная, она описывает изучаемую зависимость.
, что говорит о повышенной ошибке аппроксимации, но в допустимых пределах. Показательная функция чуть хуже, чем степенная, она описывает изучаемую зависимость.
Таблица 1.4
| Y | x | Yx | Y2 | х2 | 
| 
| 
| Ai | |
| 4,2316 | 4,5 | 19,0422 | 17,901 | 20,25 | 60,7 | 8,1 | 65,61 | 11,8 | |
| 4,0660 | 5,9 | 23,9894 | 16,532 | 34,81 | 56,4 | 4,8 | 23,04 | 7,8 | |
| 4,1374 | 5,7 | 23,5832 | 17,115 | 32,49 | 56,9 | 3,0 | 9,00 | 5,0 | |
| 3,9532 | 7,2 | 28,4256 | 15,626 | 51,84 | 55,5 | 1,2 | 1,44 | 2,1 | |
| 3,948 | 6,2 | 24,4776 | 15,984 | 38,44 | 56,4 | -1,4 | 1,96 | ||
| 4,0452 | 24,2712 | 16,362 | 60,0 | -5,7 | 32,49 | 10,5 | |||
| 3, 932 | 7,8 | 30,6696 | 15,461 | 60,84 | 57,5 | -8,2 | 67,24 | 16,6 | |
| Итого | 28,362 | 43,3 | 174,4588 | 114,981 | 274,67 | 403,4 | -1,8 | 200,78 | 56,3 |
| Среднее значение | 4, 052 | 6,186 | 24,9237 | 16,426 | 39,238 | 28,68. | 8,0 | ||

| 0,0425 | 5,86 | |||||||

| 0,0018 | 34,3396 |
1г. Уравнение равносторонней гиперболы  линеаризуется при замене:
линеаризуется при замене:  Тогда
Тогда 
Для расчетов используем данные таблицы 1.5.
Таблица 1.5
| y | z | yz | z2 | y2 | 
| 
| 
| Ai | |
| 68,8 | 0,0222 | 1,5255 | 0,000492 | 4733,44 | 61,8 | 7,0 | 49,00 | 10,2 | |
| 61,2 | 0,0169 | 1,0373 | 0,000287 | 3745,44 | 56,3 | 4,9 | 24,01 | 8,0 | |
| 59,9 | 0,0175 | 1,0472 | 0,000306 | 3588,01 | 56,9 | 3,0 | 9,00 | 5,0 | |
| 56,7 | 0,0162 | 0,9175 | 0,000262 | 3214,89 | 55,5 | 1,2 | 1,44 | 2,1 | |
| 0,0170 | 0,000289 | 3025,00 | 56,4 | -1,4 | 1,96 | 2,5 | |||
| 54,3 | 0,0212 | 1,1504 | 0,000449 | 2948,49 | 60,8 | -6,5 | 42,25 | 12,0 | |
| 49,3 | 0,0181 | 0,8931 | 0,000328 | 2430,49 | 57,5 | -8,2 | 67,24 | 16,6 | |
| Итого | 405,2 | 0,1291 | 7,5064 | 0,002413 | 23685,76 | 405,2 | 0,0 | 194,90 | 56,5 |
| Среднее значение | 57,9 | 0,0184 | 1,0723 | 0,000345 | 3383,68 | 27,84 | 8,1 | ||

| 5,74 | 0,002145 | |||||||

| 32,9476 | 0,000005 |
Значения параметров регрессии а и b составили:

Получено уравнение: 
Индекс корреляции:  Коэффициент аппроксимации:
Коэффициент аппроксимации:  . Для уравнения равносторонней гиперболы получена наибольшая оценка тесноты связи:
. Для уравнения равносторонней гиперболы получена наибольшая оценка тесноты связи:  (по сравнению с линейной, степенной и показательной регрессиями),
(по сравнению с линейной, степенной и показательной регрессиями),  остается на допустимом уровне:
остается на допустимом уровне:
2. 
где Fтабл=6,6>Fфакт, а=0,05.
где
Следовательно, принимается гипотеза Н0 о статистически незначимых параметрах этого уравнения. Этот результат можно объяснить сравнительно невысокой теснотой выявленной зависимости и небольшим числом наблюдений.
Пример 2
По территориям региона приводятся данные за 2008 г. (табл. 1.6).
Таблица 1.6
| Номер региона | Среднедушевой прожиточный минимум в день одного трудоспособного, руб., х | Среднедневная заработная плата, руб., у |
Требуется:
1. Построить линейное уравнение парной регрессии у от х.
2. Рассчитать линейный коэффициент парной корреляции и среднюю ошибку аппроксимации.
3. Оценить статистическую значимость параметров регрессии и корреляции.
4. Выполнить прогноз заработной платы у при прогнозном значении среднедушевого прожиточного минимума х, составляющем 107% от среднего уровня.
5. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал.
Решение: 1. Для расчета параметров уравнения линейной регрессии строим расчетную таблицу (табл. 1.7).
Таблица 1.7
| x | у | ух | х2 | у2 | 
| 
| 
| |
| -16 | 12,0 | |||||||
| -4 | 2,7 | |||||||
| -23 | 17,2 | |||||||
| 2,6 | ||||||||
| 1.9 | ||||||||
| 10,8 | ||||||||
| 0,0 | ||||||||
| 0,0 | ||||||||
| 5,3 | ||||||||
| 3,1 | ||||||||
| -10 | 5,8 | |||||||
| Итого | 68,8 | |||||||
| Среднее значение | 85,6 | 155,8 | 13484,0 | 7492,3 | 24531,4 | 5,7 | ||

| 12,95 | 16,53 | ||||||

| 167,7 | 273,4 |
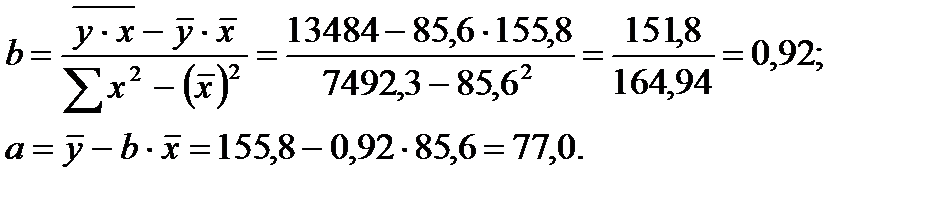
Получено уравнение регрессии: 
С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,92 руб.
2. Тесноту линейной связи оценит коэффициент корреляции:

Это означает, что 52% вариации заработной платы (у) объясняется вариацией факторах - среднедушевого прожиточного минимума. Качество модели определяет средняя ошибка аппроксимации:
Качество построенной модели оценивается как хорошее, так как  не превышает 8-1 0%.
не превышает 8-1 0%.
3. Оценку статистической значимости параметров регрессии проведем с помощью t -статистики Стьюдента и путем расчета доверительного интервала каждого из показателей.
Выдвигаем гипотезу Н0 о статистически незначимом отличии показателей от нуля:  .
.
Tтабл для числа степеней свободы  и
и  составит 2,23.
составит 2,23.
Определим случайные ошибки  :
:

Тогда 
Фактические значения t -статистики превосходят табличные значения:

поэтому гипотеза Н0 отклоняется, т.е.  и
и  не случайно отличаются от нуля, а статистически значимы.
не случайно отличаются от нуля, а статистически значимы.
Рассчитаем доверительный интервал для a и b. Для этого определим предельную ошибку для каждого показателя:

Доверительные интервалы:






Анализ верхней и нижней границ доверительных интервалов говорит о том, что с вероятностью  параметры a и b, являются статистически значимыми.
параметры a и b, являются статистически значимыми.
4. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит:  тыс. руб., тогда прогнозное значение прожиточного минимума составит:
тыс. руб., тогда прогнозное значение прожиточного минимума составит:
 тыс. руб.
тыс. руб.
5. Ошибка прогноза составит с учетом e:
 тыс. руб.
тыс. руб.
Предельная ошибка прогноза, которая в 95% случаев не будет превышена, составит:

Доверительный интервал прогноза:

 руб.;
руб.;  руб.
руб.
Выполненный прогноз среднемесячной заработной платы оказался надежным  , но недостаточно точным, так как диапазон верхней и нижней границ доверительного интервала
, но недостаточно точным, так как диапазон верхней и нижней границ доверительного интервала  составляет 1,95 раза:
составляет 1,95 раза:

Пример 3. По группе предприятий, производящих однородную продукцию, известно, как зависит себестоимость единицы продукции у от факторов, приведенных в табл. 1.8.
Таблица 1.8
| Признак-фактор | Уравнение парной регрессии | Среднее значение фактора |
| Объем производства, млн руб., х1 | 
| 
|
| Трудоемкость единицы продукции, чел.-час, х2 | 
| 
|
| Оптовая цена за 1 т энергоносителя, млн. руб., х3 | 
| 
|
| Доля прибыли, изымаемой государством, %, х4 | 
| 
|
Требуется:
1. Определить с помощью коэффициентов эластичности силу влияния каждого фактора на результат.
2.Ранжировать факторы по силе влияния.
Решение:
1. Для уравнения равносторонней гиперболы 

Для уравнения прямой 

Для уравнения степенной зависимости 


Для уравнения показательной зависимости  :
:

2. Сравнивая значения  , ранжируем xj по силе их влияния на себестоимость единицы продукции:
, ранжируем xj по силе их влияния на себестоимость единицы продукции:
а)  ; в)
; в)  ;
;
б)  ; г)
; г)  .
.
Для формирования себестоимости продукции группы предприятий первоочередное значение имеют цены на энергоносители; в гораздо меньшей степени влияют трудоемкость продукции и отчисляемая часть прибыли. Фактором снижения себестоимости выступает размер производства: с ростом его на 1% себестоимость единицы продукции снижается на -0,97%.
Пример 4. Зависимость потребления продукта А от среднедушевого дохода по данным 20 семей характеризуется следующим образом:
уравнение регрессии  ;
;
индекс корреляции  ;
;
остаточная дисперсия  .
.
Требуется: Провести дисперсионный анализ полученных результатов.
Решение: Результаты дисперсионного анализа приведены в табл. 1.9.
Таблица 1.9
| Вариация результата у | Число степеней свободы | Сумма квадратов отклонений, S | Дисперсия на одну степень свободы, D | Fфакт | Fтабл

|
| Общая | 
| 6,316 | – | – | – |
| Факторная | 
| 5,116 | 5,116 | 76,7 | 4,41 |
| Остаточная | 
| 1,200 | 0,0667 | – | – |

В силу того что Fфакт = 76,7 > Fтабл = 4,4, гипотеза о случайности различий факторной и остаточной дисперсий отклоняется. Эти различия существенны, статистически значимы, уравнение надежно, значимо, показатель тесноты связи надежен и отражает устойчивую зависимость потребления продукта А от среднедушевого дохода.
Задача 14.
Определить зависимость урожайности озимой пшеницы от количества внесенных удобрений  ,где х - количество удобрений в центнерах (ц) на 1 гектар (га), у - урожайность в ц на 1 га.
,где х - количество удобрений в центнерах (ц) на 1 гектар (га), у - урожайность в ц на 1 га.
| х | |||||
| у |
Расчетная таблица
| х | у | х2 | х3 | х4 | ху | ух2 | 
|
| 
| |
| 6,2 | -0,2 | 0,04 | ||||||||
| 8,5 | 0,5 | 0,25 | ||||||||
| 10,4 | -0,4 | 0,16 | ||||||||
| 11,9 | 0,1 | 0,01 | ||||||||
| 13,0 | ||||||||||
| 0,46 |
МНК для модели:

 (*)
(*)
Решаем систему (*), методом треугольников, получим:



 – уравнение регрессии.
– уравнение регрессии.
