Введение в эконометрику.

Методические указания

К самостоятельной работе

по дисциплине «Эконометрика»

Направление подготовки: 38.03.01 «Экономика»

Профили подготовки: «Финансы и кредит», «Бухгалтерский учет, анализ и аудит», «Налоги и налогообложение»

 

Квалификация (степень) выпускника: 63 бакалавр

Форма обучения: заочная

 

 

Тула 2017

 

 

Методические указания для практических занятий рассмотрены и утверждены на заседании кафедры «Финансы и менеджмент» института права и управления,

протокол № _1_ от” _30_” августа_ 2017_г.

Зав. кафедрой __________________________А.Л. Сабинина

 

 

Тема 1. Линейная модель парной регрессии. МНК.

Введение в эконометрику.

Курс предполагает знание разделов математики:

а) Линейная алгебра: Векторное пространство, линейное подпространство, базис, размерность. Линейные операторы. Матрицы, операции с матрицами, ранг и обратная матрица. Системы линейных уравнений. Собственные векторы и собственные числа линейных операторов.

б) Математическая статистика:

Операция суммирования.

Пусть величина X задается последовательностью данных x_1,x_2,…,x_n.,каждое из которых можно записать как x_i, 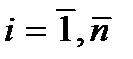. Сумма`этих чисел обозначается следующим образом:

Если из контекста ясно, каковы начальный и конечный суммируемые члены, то часто используют сокращенные обозначения

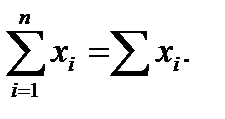
Сумма квадратов этих чисел обозначается следующим образом

Обозначим средние величины X, X² и XY соответственно как: 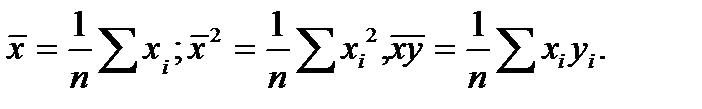Имеет место неравенство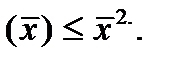

Правила суммирования (a,b –константы):

.

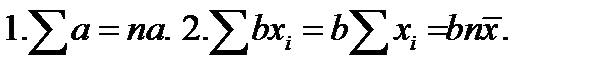
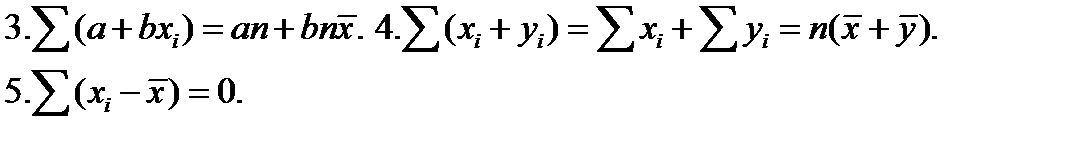
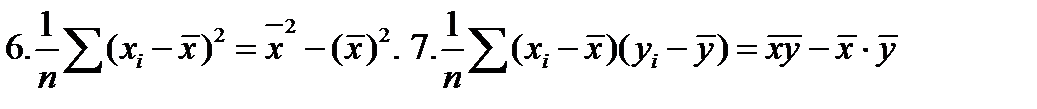в) Теория вероятностей: Случайные величины (СВ), дискретные непрерывные, их характеристики и свойства. Функция распределения СВ и ее плотность распределения. Ковариация. Дисперсия и корреляция. Законы распределения СВ. Случайной величиной (переменной) называется величина, которая под воздействием случайных факторов может с определенными вероятностями принимать те или иные значения из некоторого множества чисел. Случайные величины обозначаются большими буквами, а их возможные значения – малыми.

Для полной характеристики СВ указываются не только ее значения, но и их вероятности. Универсальным способом задания СВ X является задание ее функции распределения.

Функцией распределения F(x) СВ X называется вероятность того, что величина X принимает значение меньшее x, т.е. F(x)=P(X<x), x? R.

Свойства функции распределения:

1.0≤F(x)≤1 при любых x? R.

2. P(x₁≤X≤x₂) = F(x₂) – F(x₁).

3. F(x) – неубывающая функция.

4. lim F(x) =0, lim F(x) = 1

_{x→-∞ x →∞}

СВ бывают дискретными и непрерывными.

Дискретной называется СВ, которая принимает отдельные, изолированные друг от друга значения. Число возможных значений ДСВ конечно и счетно. Ее лучше задавать не в виде функции распределения, а в виде ряда распределения. При табличном задании ряда распределения первая строка таблицы содержит возможные значения СВ, а вторая – соответствующие им вероятности, т.е. p_i = P(X =x_i), Sp_i= 1.

Пример: Случайная величина Х задана ряда распределения:

 

ХX
Рp	0,1	0.2	0,3	0.4

 

Найти математическое ожидание, дисперсию и среднеквадратическое отклонение СВ Х, функцию распределения F(x).

1) М(Х)=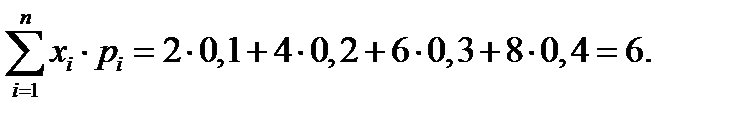

2)

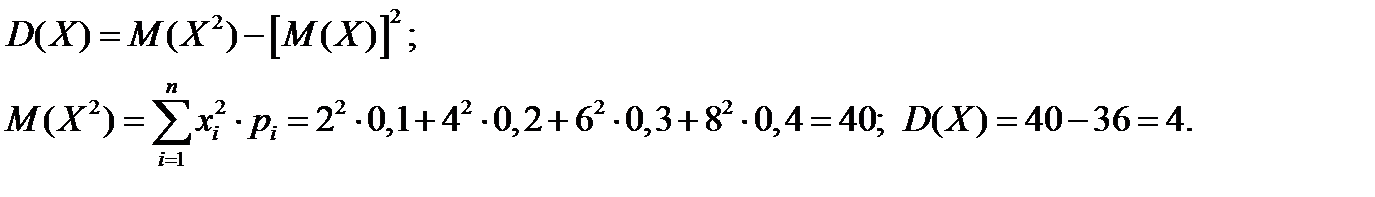
3)

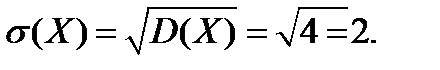
4)

 

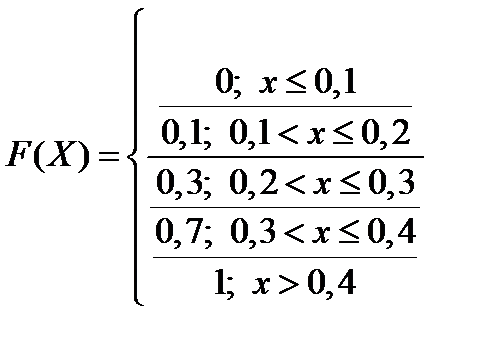
При табличном задании ряда распределения первая строка таблицы содержит возможные значения СВ, а вторая – соответствующие им вероятности, т.е. p_i = P(X =x_i), Sp_i= 1.

Графическое изображение ряда распределения называется полигоном распределения.

Непрерывной называется СВ, множество значений которой непрерывно заполняет некоторый числовой промежуток. Число возможных значений НСВ бесконечно.

Задать НСВ рядом распределения невозможно, поэтому ее задают функцией распределения F(x). Вместо вероятности НСВ используют плотность распределения вероятностей f(x). Плотность вероятности определяется: f(x) = F’(x). Из определения производной вытекает

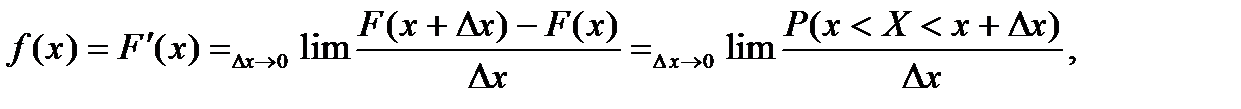
т.е. предел отношения вероятности попадания СВ X в интервал (x,x+Dx) к длине этого интервала при Dx→0 равен значению плотности распределения вероятностей f(x).

Свойства плотности распределения:

1. f(x) ≥ 0 при любых x? R.

2. P(x₁≤X≤x₂) =

3.

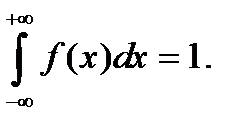
В основе математической статистики лежат понятия генеральной и выборочной совокупностей.

Генеральная совокупность – это множество всех значений (исходов) СВ, которые она может принять в процессе наблюдения. Например, данные о доходах всех жителей страны.

Выборочная совокупность (выборка) – это множество наблюдений, составляющих лишь часть генеральной совокупности. Для СВ важную роль помимо функции распределения играют числовые характеристики ее распределении.

Числовые характеристики распределения.

I. Генеральная совокупность

Математическим ожиданием ДСВ называется сумма произведений всех ее значений на соответствующие им вероятности, т.е.

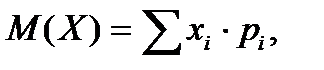где суммирование осуществляется по всем возможным значениям СВ.

Математическое ожидание НСВ определяется выражением 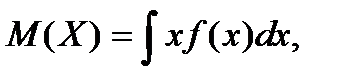где интегрирование осуществляется на всем интервале, в котором определена

Математическое ожидание СВ – это среднее ее значение по генеральной совокупности, обозначается 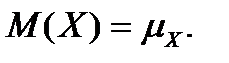Геометрически математическое ожидание СВ – это центр ее распределения.

Свойства математического ожидания (a,b – константы; X,Y – CВ);

1. M(a) = a

2. M(bX) = bM(X).

3. M(a+bX) = a + bM(X).

4. M(X + Y) = M(X) + M(Y).

5.

Математическое ожидание функции g(X) определяется выражением

где суммирование осуществляется по всем возможным значениям 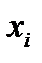. В частности, если 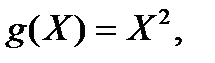то 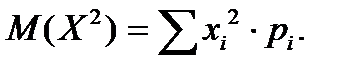Случайные величины X,Y называются независимыми, если 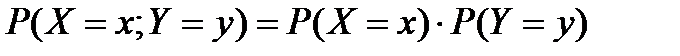для любых значений x,y.

Следствие. Если СВ X,Y независимы, то

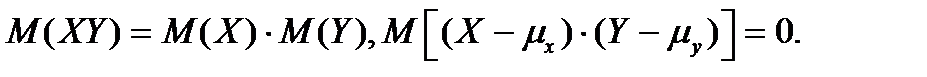
Теоретическая (генеральная) дисперсия СВ определяется как математическое ожидание квадрата отклонения СВ X относительно ее средней, т.е.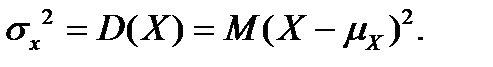

Замечание. Если ясно, о какой переменной идет речь, нижний индекс в

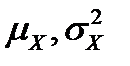можно не указывать.

Для вычисления дисперсии часто используется другое выражение, получаемое из определения дисперсии:

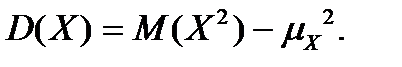
Дисперсия является мерой рассеяния СВ относительно средней (центра). Размерность дисперсии не совпадает с размерностью СВ.

Стандартным отклонением СВ X называется корень квадратный из ее дисперсии, т.е. 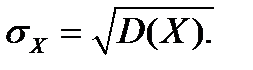Стандартное отклонение показывает, насколько в среднем отклоняется СВ в совокупности относительно средней (центра).

Свойства дисперсии:

1. D(a) = 0.

2. D(bX)= b²D(X).

3. D(a + bX) = b²D(X).

Следствие. Если СВ X,Y независимы, то 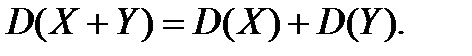Заметим, что M(X) и D(X) – это числовые характеристики генеральной совокупности (числа), а не функции.

Нормальное распределение СВ X характеризуется лишь двумя параметрами: средним значением и дисперсией Это обозначается как X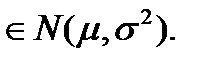

График плотности нормального распределения f(x) колоколообразный симметричный вид. Максимум этой функции находится в точке x =μ, а разброс

Относительно этой точки определяется параметром σ. Чем меньше значение s

, тем более острый и высокий максимум f(x).

П. Выборочная совокупность.

Пусть из генеральной совокупности с распределением F(X) извлекается выборка объема n. Считаем, что выборочные наблюдения X₁,X₂,…X_n независимы и имеют одинаковые распределения.

Выборочной средней называется среднее арифметическое наблюдаемых значений СВ в выборке, т.е.

.

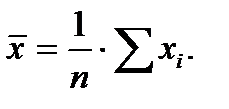Выборочной дисперсией (вариацией) называется среднее арифметическое квадратов отклонений наблюдаемых значений СВ от среднего значения, т.е.

.

Свойства выборочной дисперсии:

.

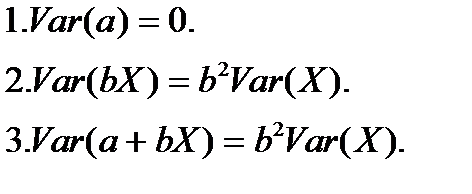Значения `x, Var(X) являются числовыми характеристиками выборочной совокупности.

Для разных выборок, взятых из одной и той же генеральной совокупности выборочные средние и выборочные дисперсии будут различны, т.е. выборочные характеристики являются СВ. Из условия, что все выборочные наблюдения X₁,X₂,…X_n независимы и имеют одинаковые распределения, вытекают следующие соотношения: 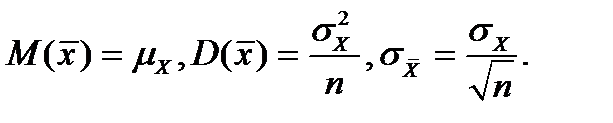Центральная предельная теорема закона больших чисел устанавливает, что распределение средней выборочной `x при достаточно большом n является нормальным, т.е.

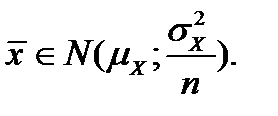
Пример: Вычислить выборочные характеристики по исходным данным

 

№ п\п
Х

 

Исходные данные (х) и расчетные показатели (х²) представить в виде расчетной таблицы:

№п\п х х²

1 2 4

2 6 36

3 10 100

4 14 196

5 18 324

Итого 50 660

Среднее 10 132

Выборочные характеристики:

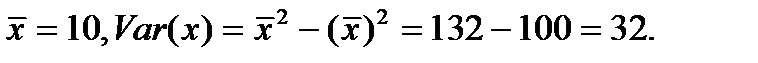
Задача 1.

Определить выборочную ковариацию и построить диаграмму рассеяния между потребительскими расходами на бензин и его реальной ценой в США с 1973-1982 гг.

 

 

Год	Расходы (млрд. долл.)	Индекс реальных цен
	26,2 24,8 25,6 26,8 27,7 28,3 27,4 25,1 25,2 25,6	103,5 127,0 126,0 124,8 124,7 121,6 149,7 188,8 193,6 173,9

 

Выборочная ковариация является мерой взаимосвязи между двумя переменными. На рисунке 1 эти данные представим в виде диаграммы рассеяния.

 

Р

180 140 25 26 27 28 У

 

Рис. 1. Диаграмма рассеяния

Показатель выборочной ковариации позволяет выразить данную связь единым числом. Для его вычисления находим сначала среднее значение цены и спроса на бензин. Затем заполняем таблицу для расчета.

 

, , ; .

 

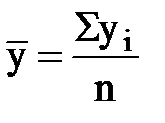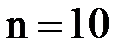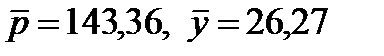Показатель выборочной ковариации позволяет выразить данную связь единым числом. Для его вычисления находим сначала среднее значение цены и спроса на бензин. Затем заполняем таблицу для расчета.

 

, , ; .

 

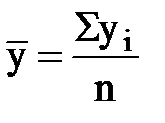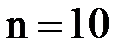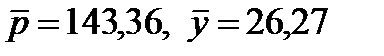Таблица для расчета:

Год	р	у
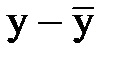
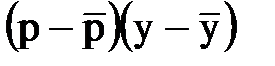
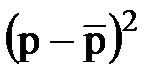
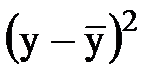
	103,5 127,0 126,0 124,8 124,7 121,6 149,7 188,8 193,6 173,9	26,2 24,8 25,6 26,8 27,7 28,3 27,4 25,1 25,2 25,6	-39,86 -16,36 -17,36 -18,56 -18,66 -21,76 6,34 45,44 50,24 30,54	-0,07 -1,47 -0,67 0,53 1,43 2,03 1,13 -1,17 -1,07 -0,67	2,79 24,05 11,63 -9,84 -26,68 -44,17 7,16 -53,16 -53,76 -20,46	1588,82 267,65 301,37 344,47 348,20 473,50 40,20 2064,79 2524,06 932,69	0,01 2,16 0,45 0,28 2,05 4,12 1,28 1,37 1,15 0,45
Сумма	1433,6	262,7			-162,44	8885,75	13,30
Среднее	143,36	26,27			-16,24	888,58	1,33

Затем вычисляем отклонения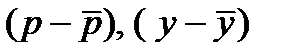

б) выборочная дисперсия;

;

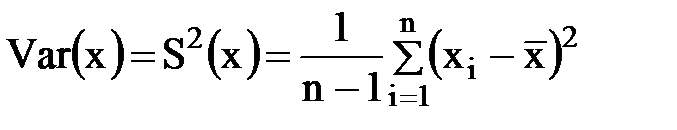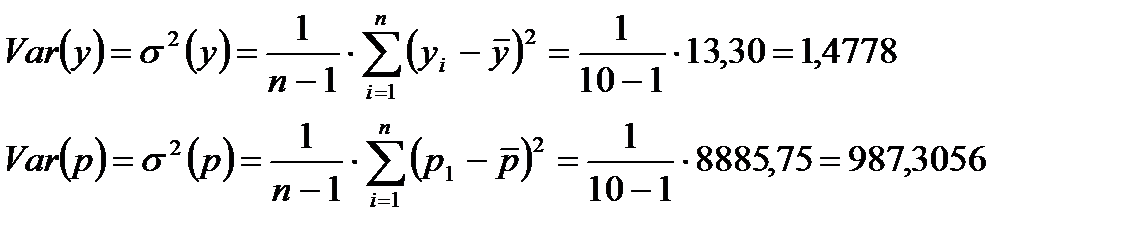
Найдем произведение по годам, сложим их и найдем среднее значение. Эта величина называется выборочной ковариацией.

в) выборочна ковариация:

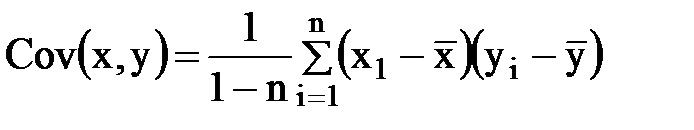
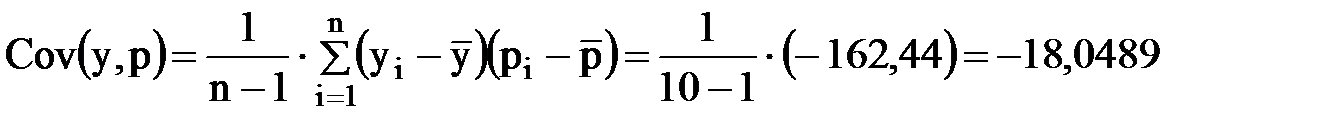
Отрицательная связь выражается отрицательной ковариацией.

г) выборочный коэффициент корреляции:

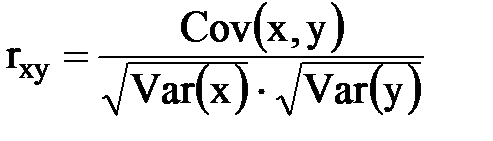. Для нашей задачи:

.

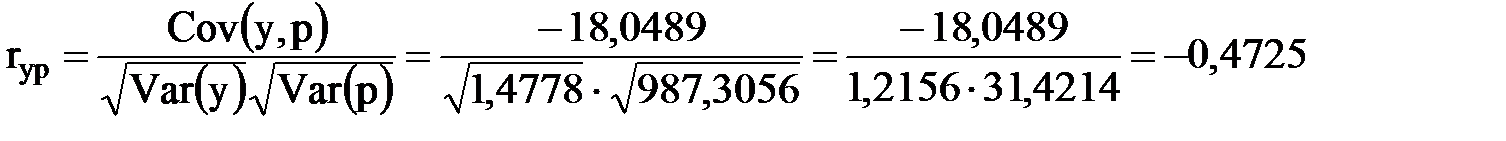Коэффициент r_yp является безразмерной величиной и измеряется в пределах от .

Для характеристики степени или силы связи используют шкалу Чеддока

Показатель тесноты связи	0,1-0,3	0,3-0,5	0,5-0,7	0,7-0,9	0,9-0,999
Характеристика силы связи	слабая	умеренная	заметная	высокая	весьма высокая

 

Значит у нас получилась связь умеренная линейная, а знак минус говорит о том, что в уравнении регрессии коэффициент при х имеет знак минус, т.е. , такая связь называется обратной.

Если r_ху>0, то говорят, что связь прямая.

Задача 2.

Найти коэффициент корреляции между производительностью труда У (тыс. руб.) и энерговооруженностью труда Х (кВт) (в расчете на одного работающего) для 14 предприятий региона по следующим данным:

Хi	2.8	2.2	3.0	3.5	3.2	3.7	4.0	4.8	6.0	5.4	5.2	5.4	6.0	9.0
Yi	6.7	6.9	7.2	7.3	8.4	8.8	9.1	9.8	10.6	10.7	11.1	11.8	12.1	12.4

Ответ: 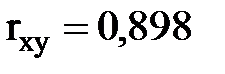связь прямая, высокая