Алгоритм обратного распространения — backpropagation algorithm — основывается на многослойной нейронной сети. В нём используется не менее трёх слоёв нейронов. Для простоты мы трёхслойные сети и будем рассматривать. Три слоя: входной, скрытый и выходной.
Таким образом на выходном слое:
на скрытом слое:
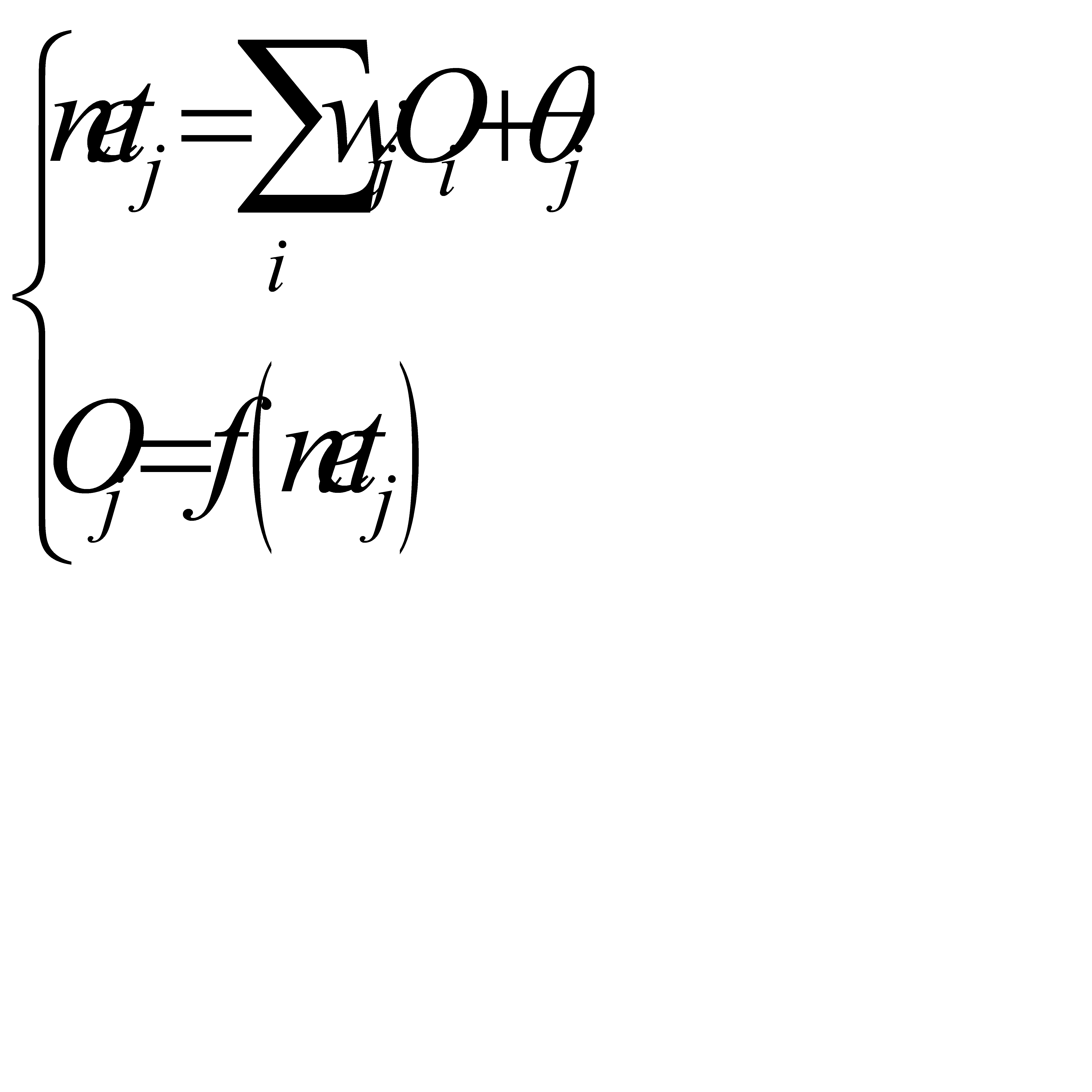
где
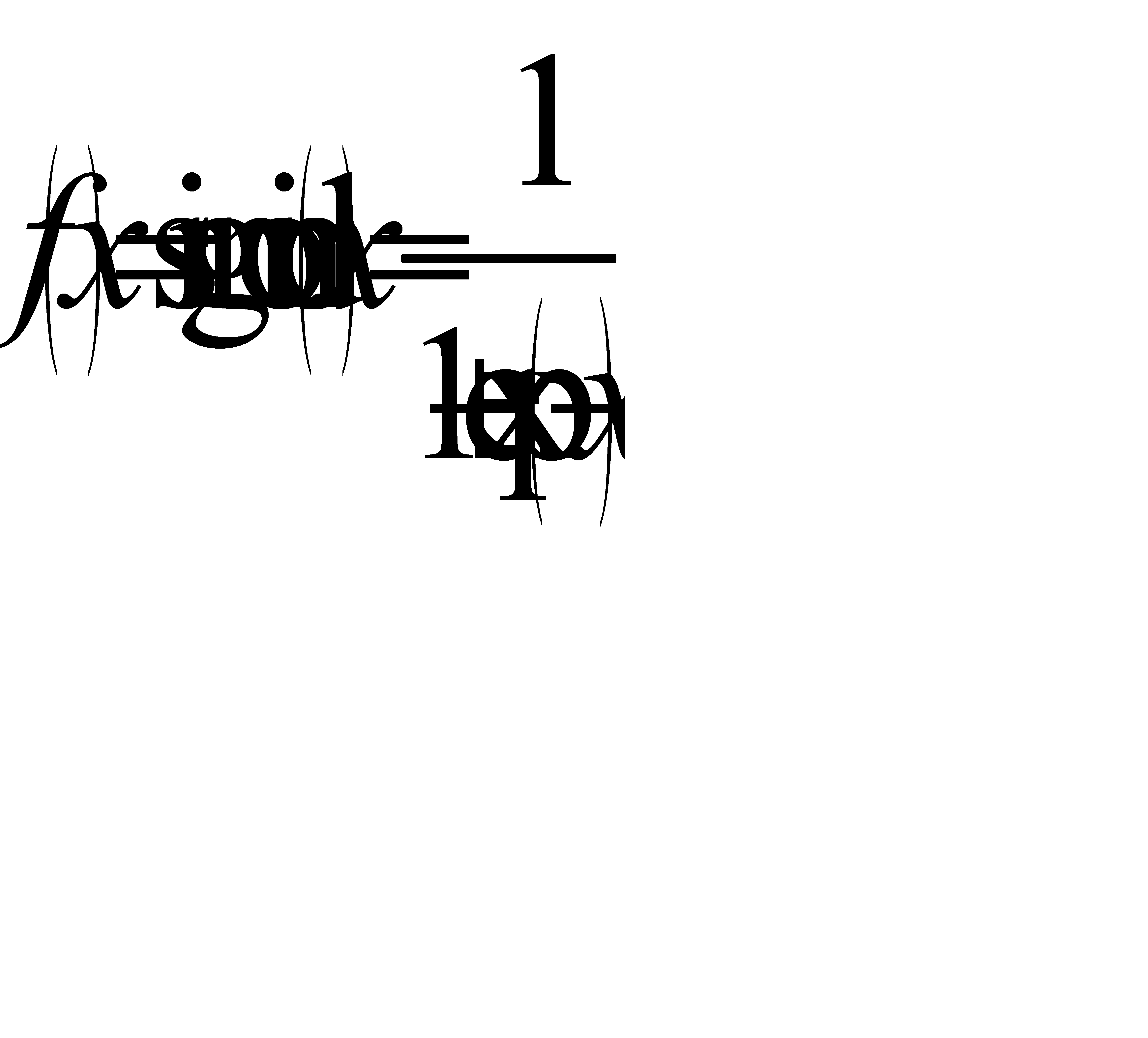
Процедура обучения включает представление набора пар входных и выходных образов. Т.е. мы должны показать нашей нейросети, что должно быть на выходе, когда на входе какая-то комбинация сигналов. Сначала нейронная сеть на основе входного образа создаёт собственный выходной образ, а затем сравнивает его с целевым выходным образом. Если различий между фактическим и целевым образами нет, то обучения не происходит. В противном случае веса связей изменяются таким образом, чтобы различие уменьшилось. Мерой различия при этом является функция квадрата ошибки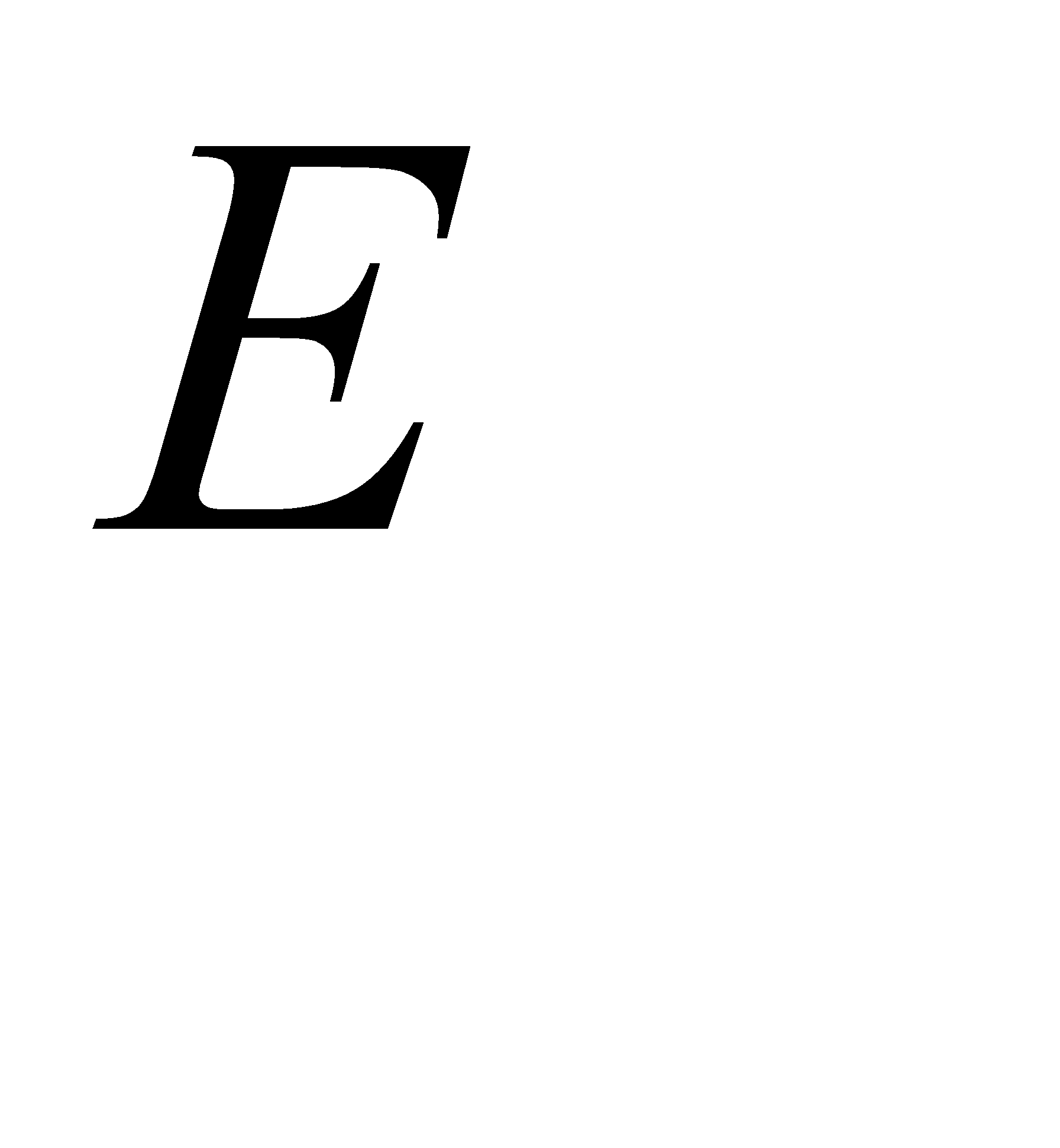 
, задаваемая следующим образом:
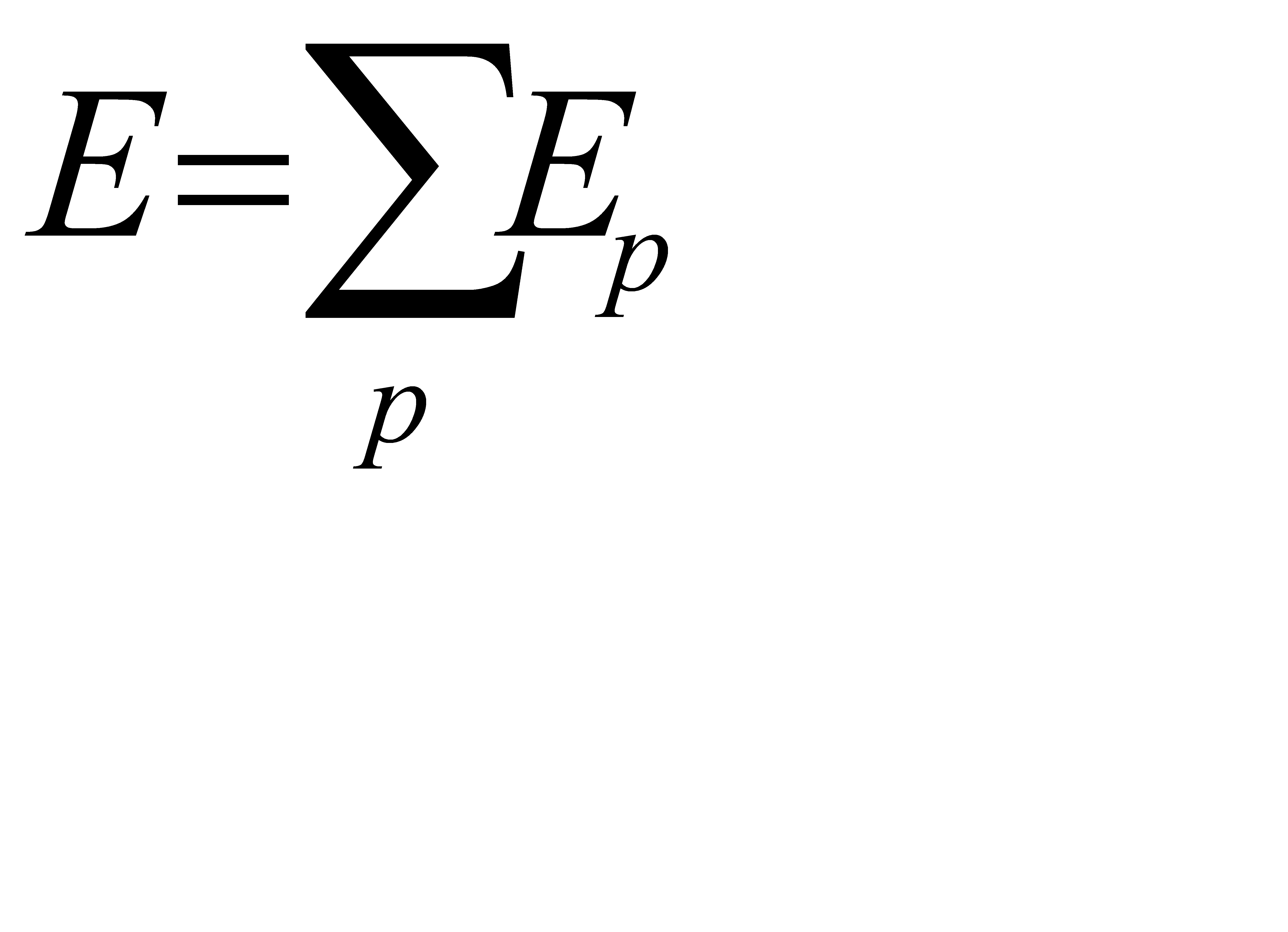
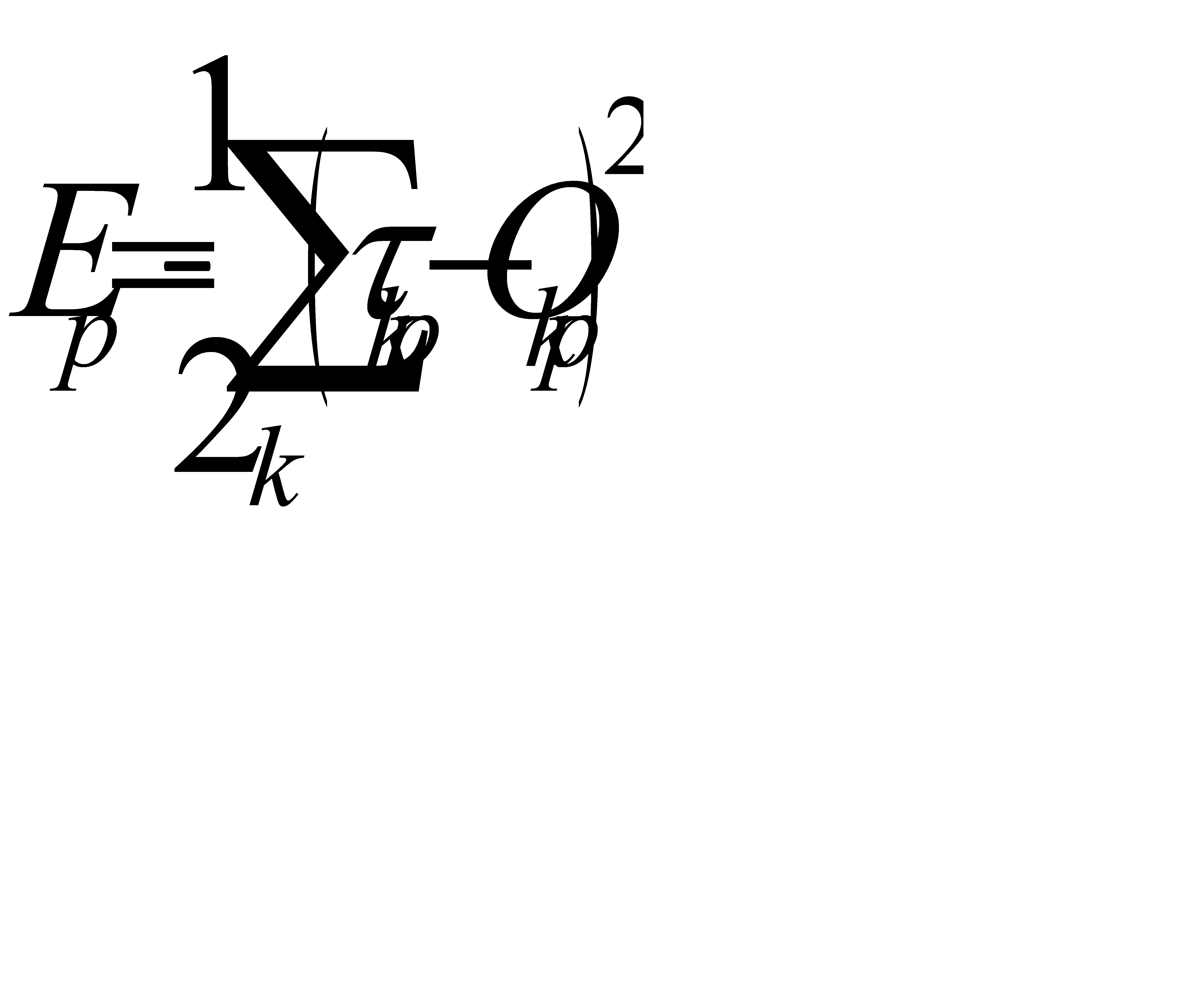
где
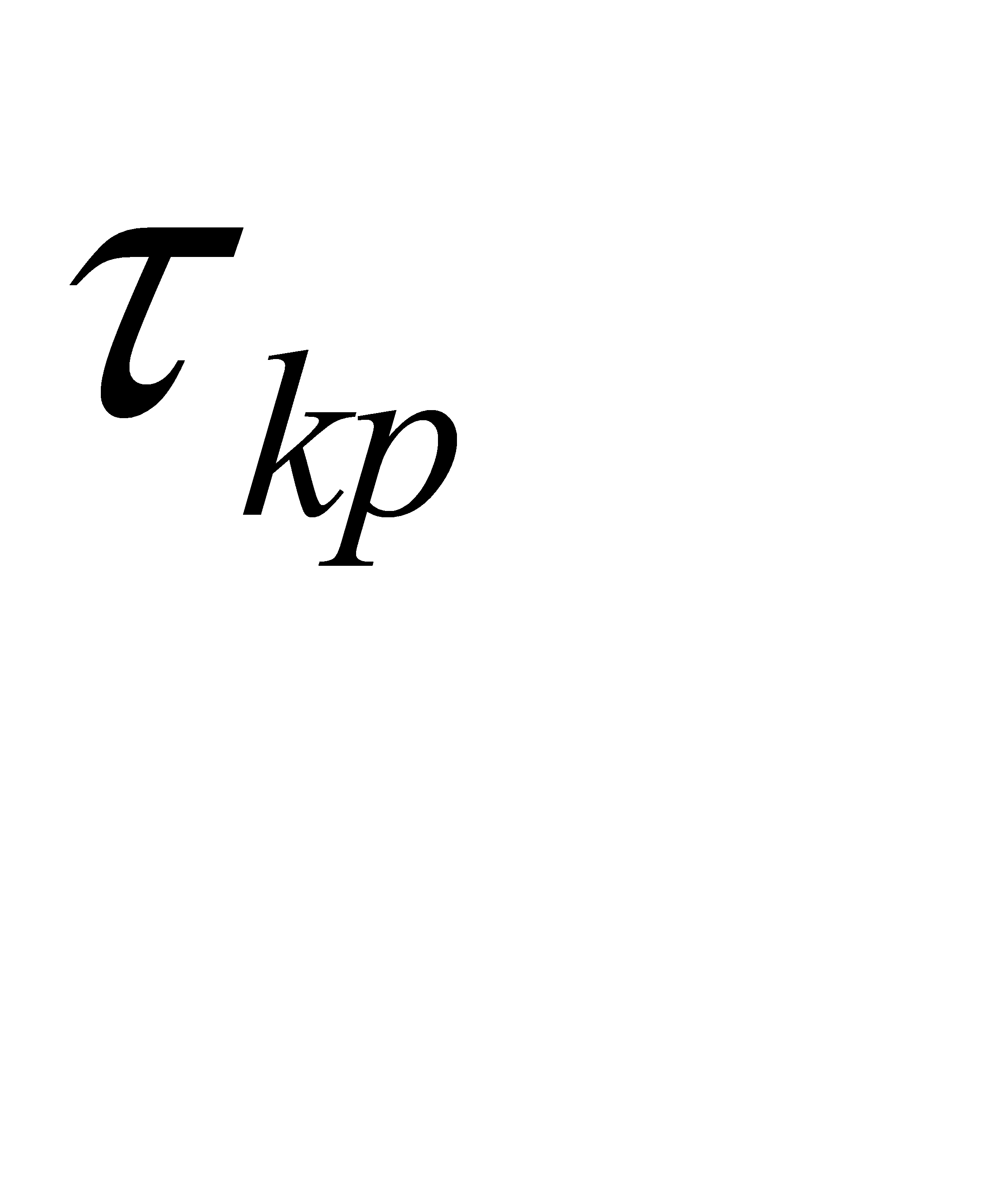— желаемый вход для 
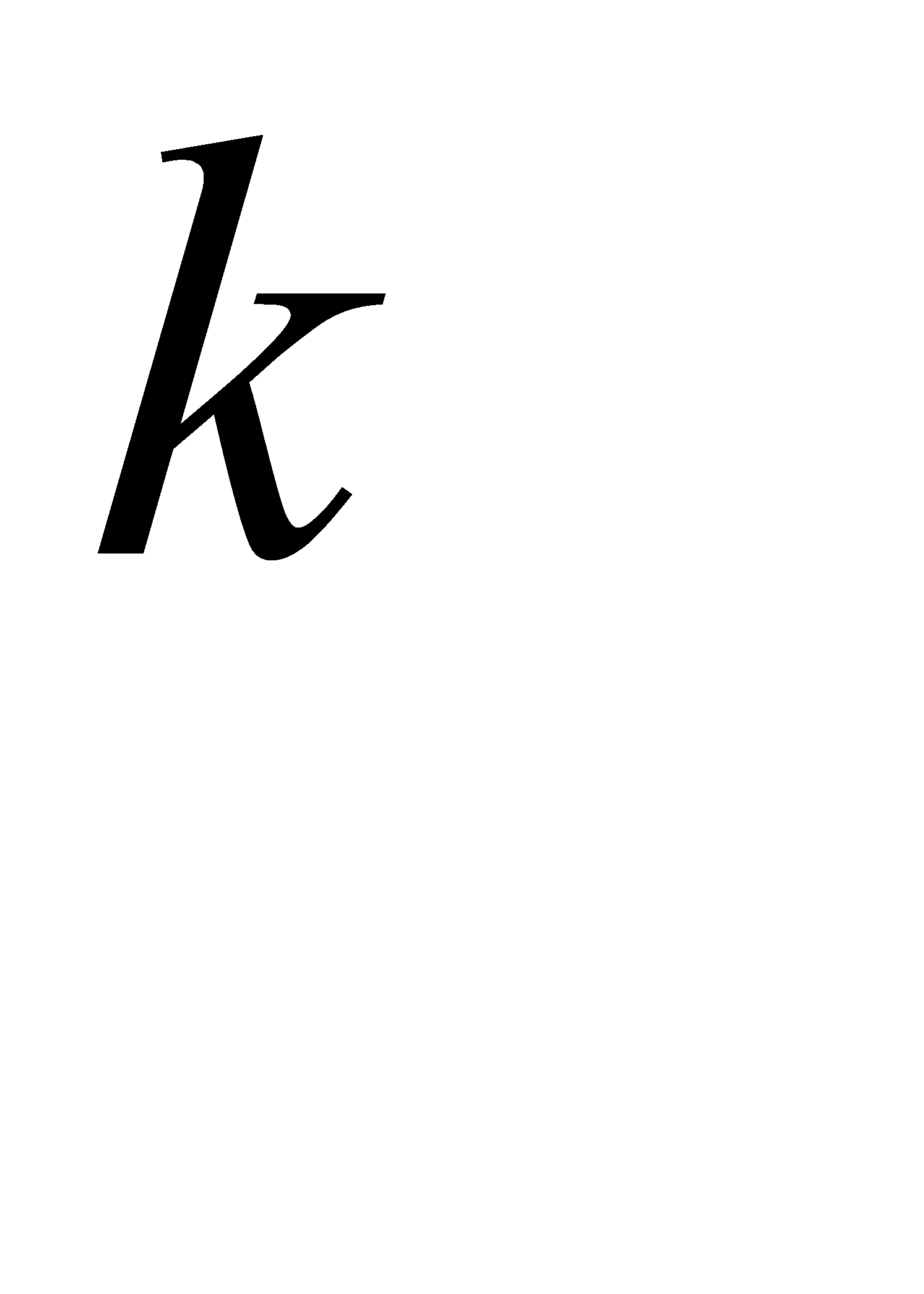-й компоненты 
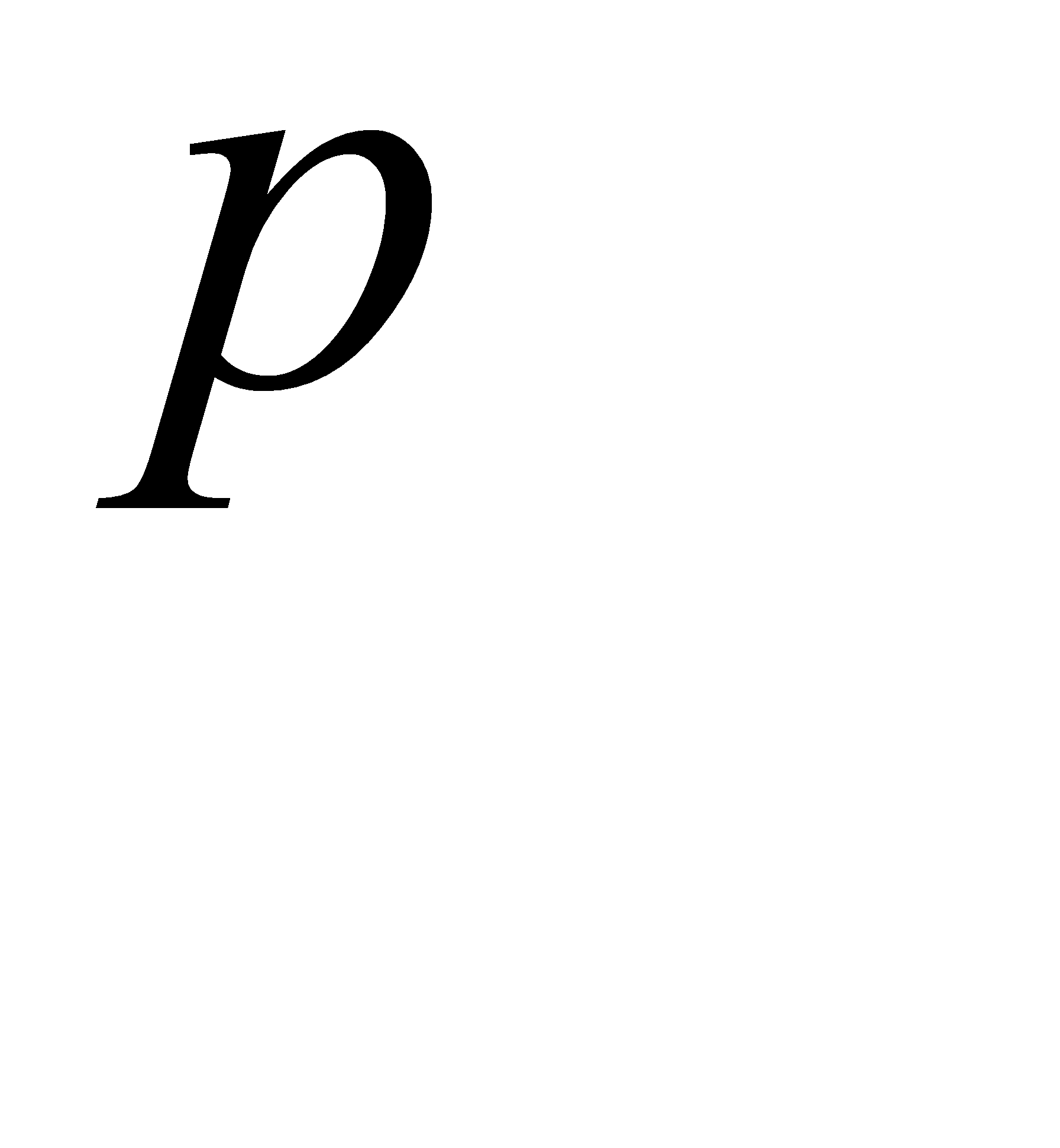-го выходного образа,
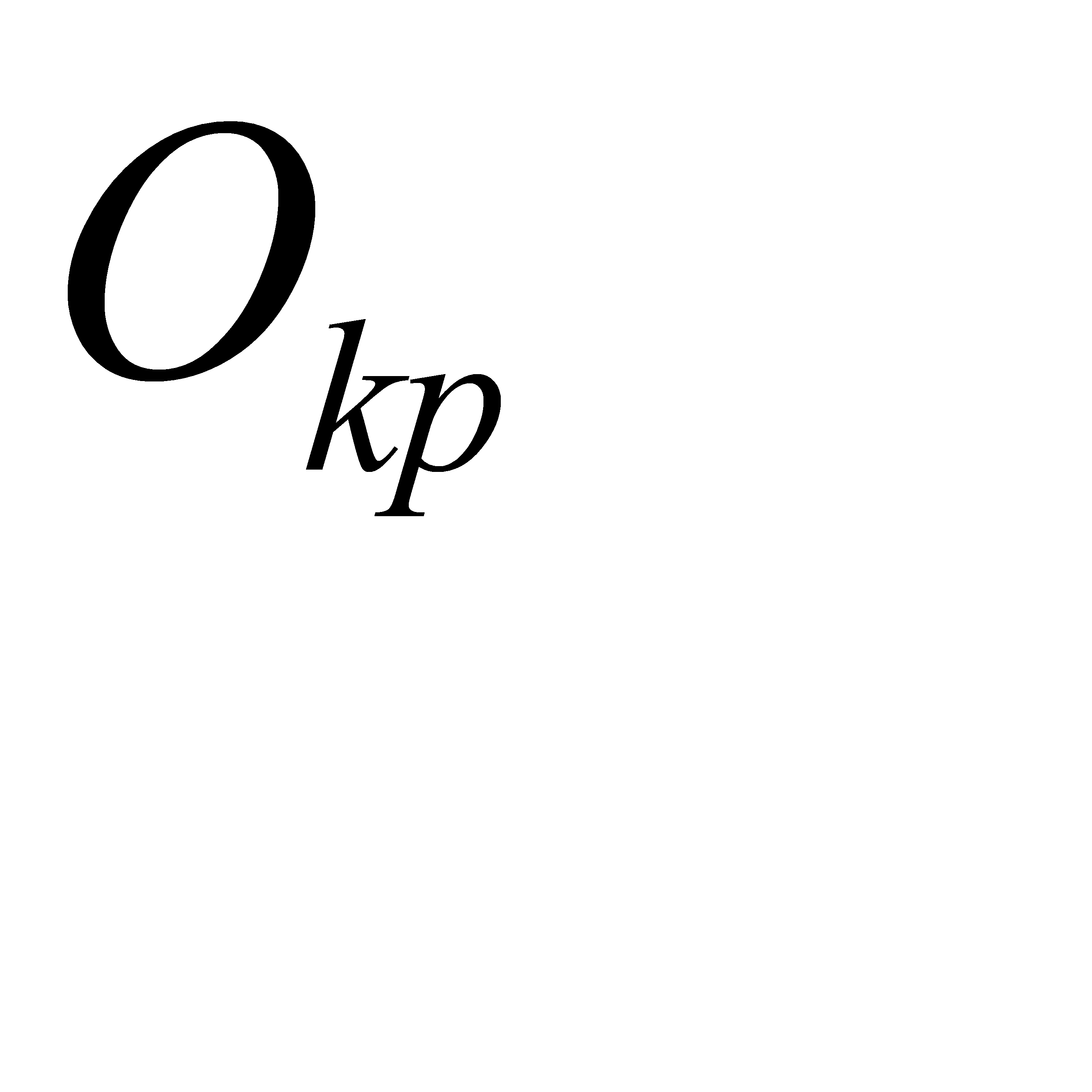— соответствующий фактический выход.
Таким образом,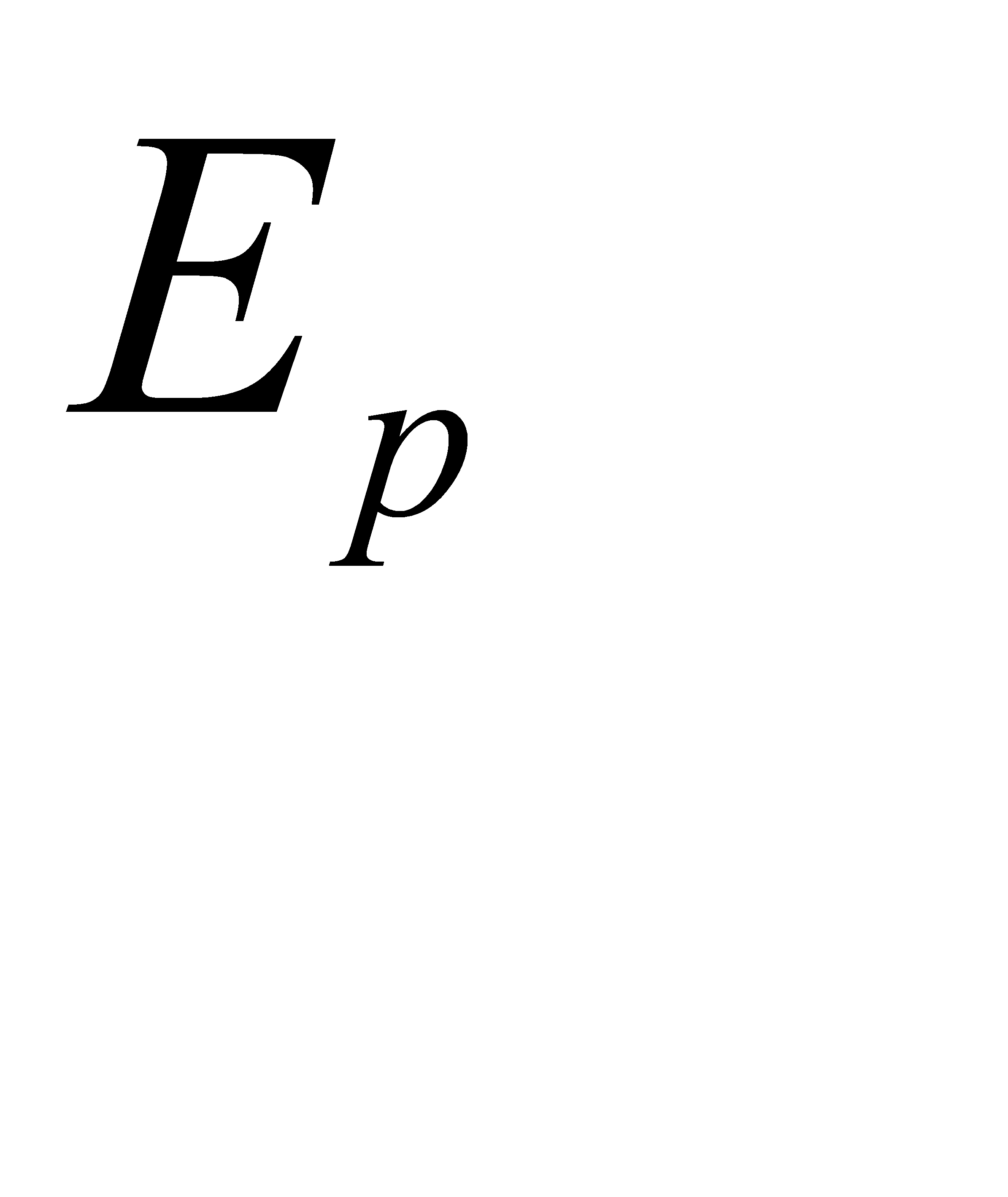 
— мера ошибки вход-выход для 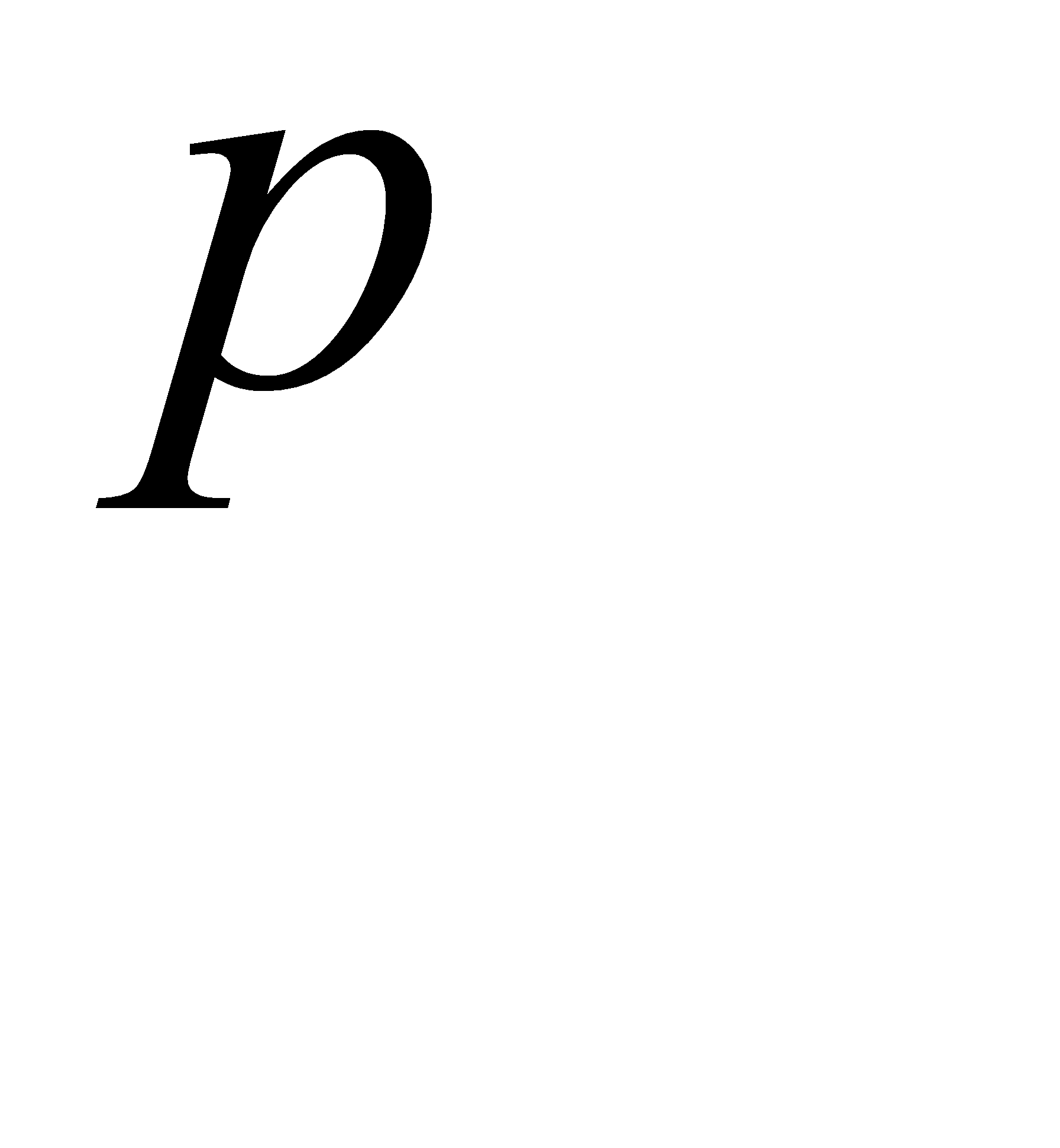-го образа, а 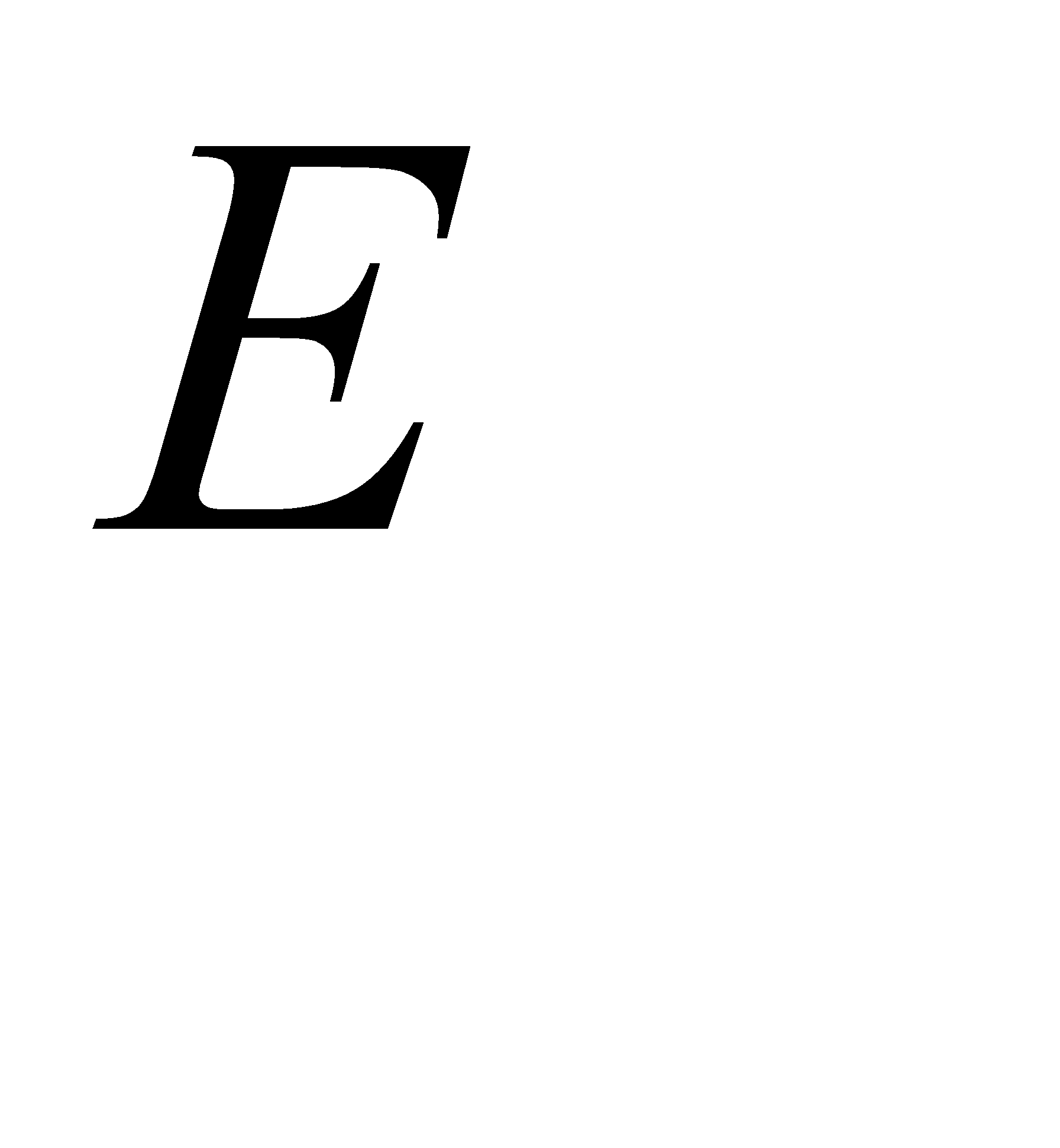— общая мера ошибки.
Задача алгоритма — добиться минимума этой ошибки, управляя весовыми коэффициентами. Можно воспользоваться градиентным методом наискорейшего спуска.
{рисунок}
Я не буду здесь подробно расписывать правила для входных и выходных слоёв, чтобы не загружать вас лишней математикой. А сразу перейду к порядку реализации алгоритма обратного распространения.
Алгоритм этот может быть представлен в виде следующих шагов:
Шаг 1. Присвоить начальные значения величинам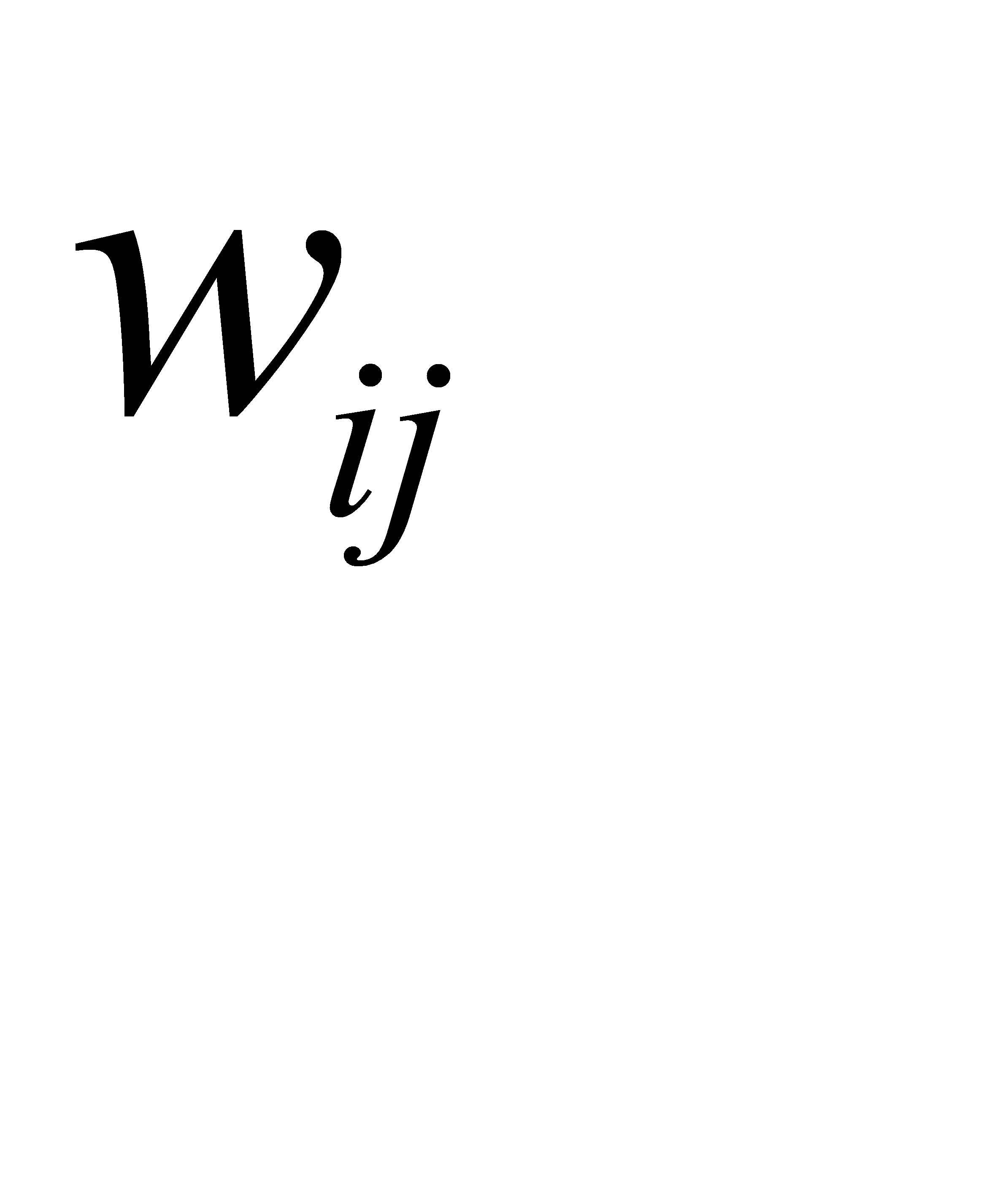 
, 
, 
, 
, 
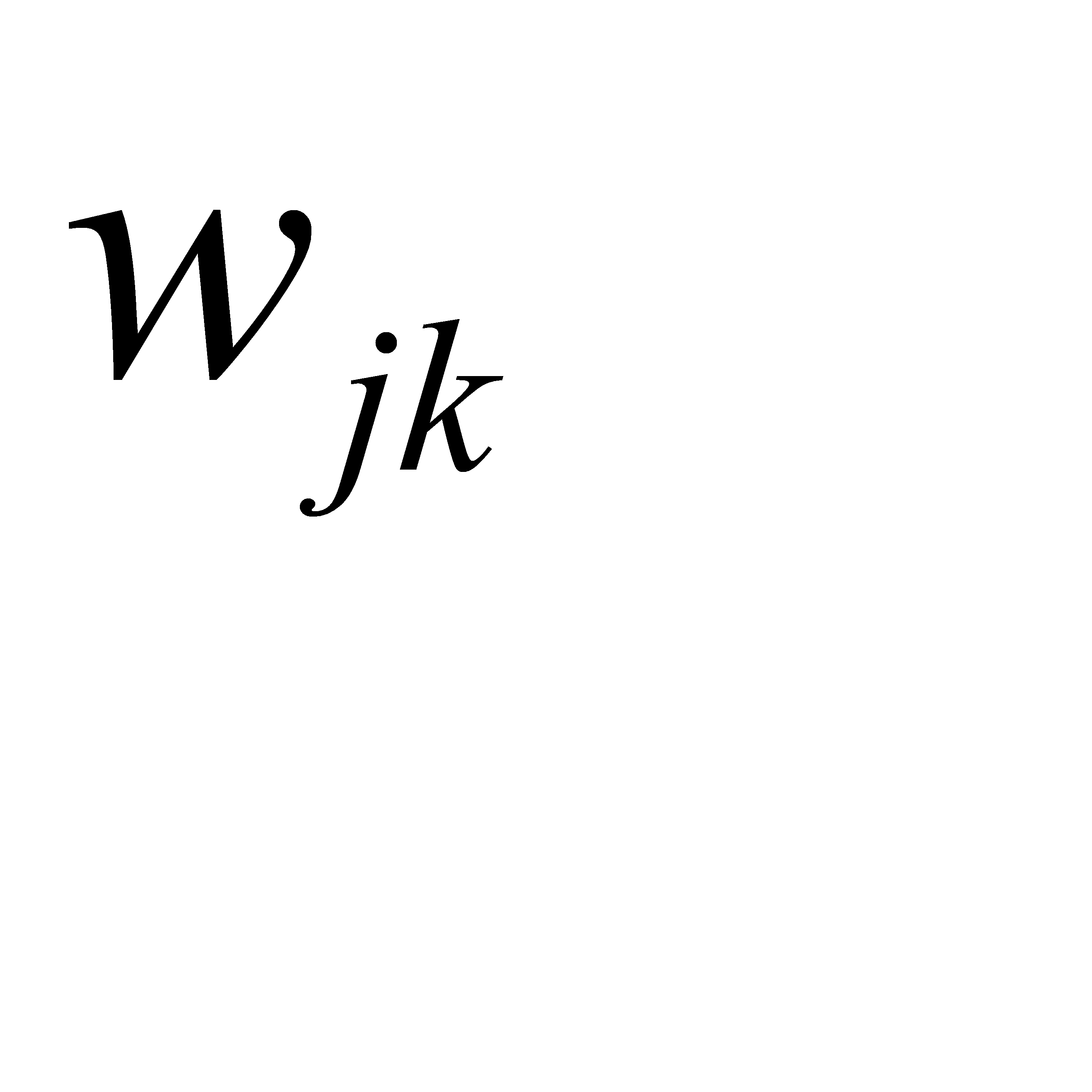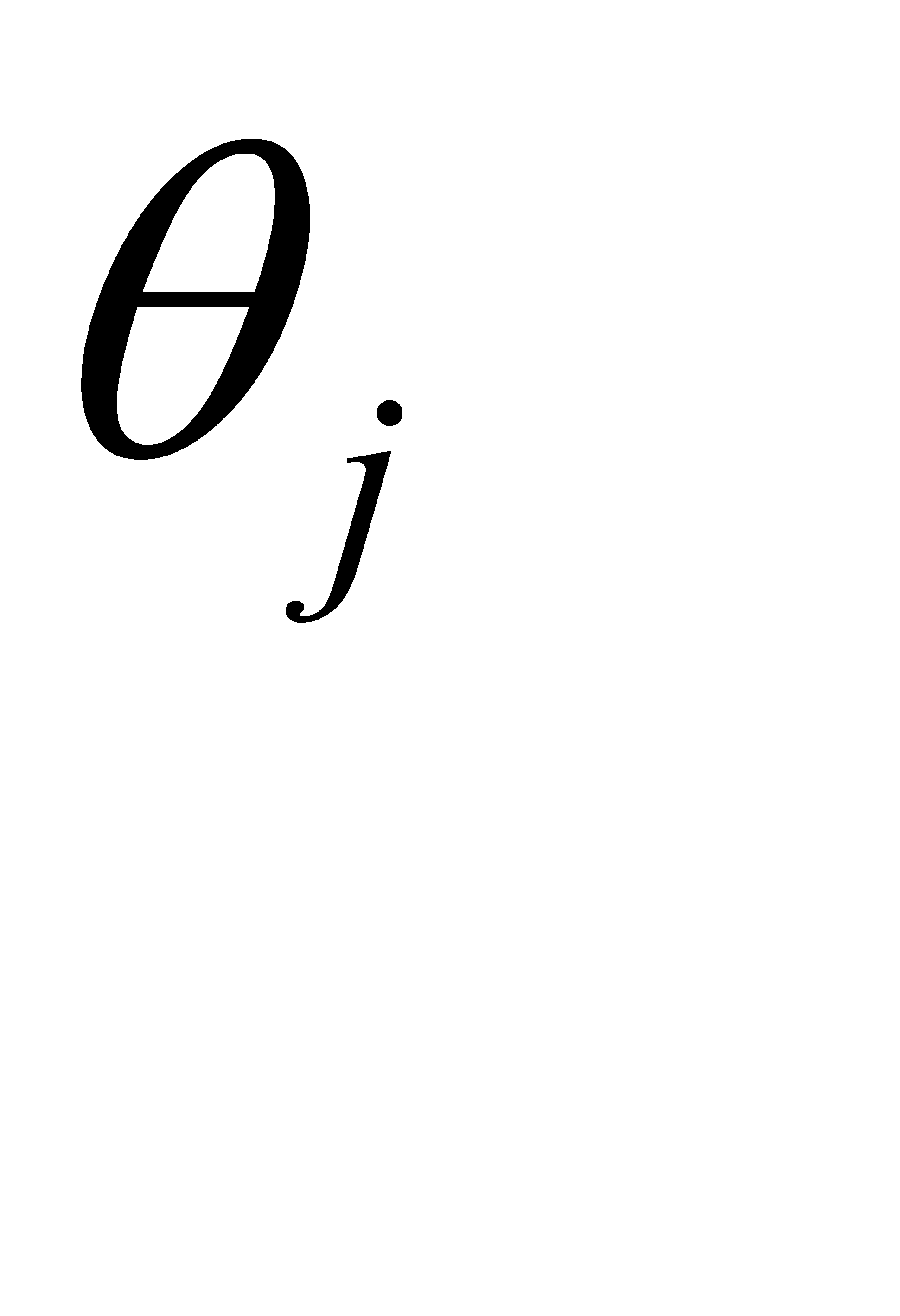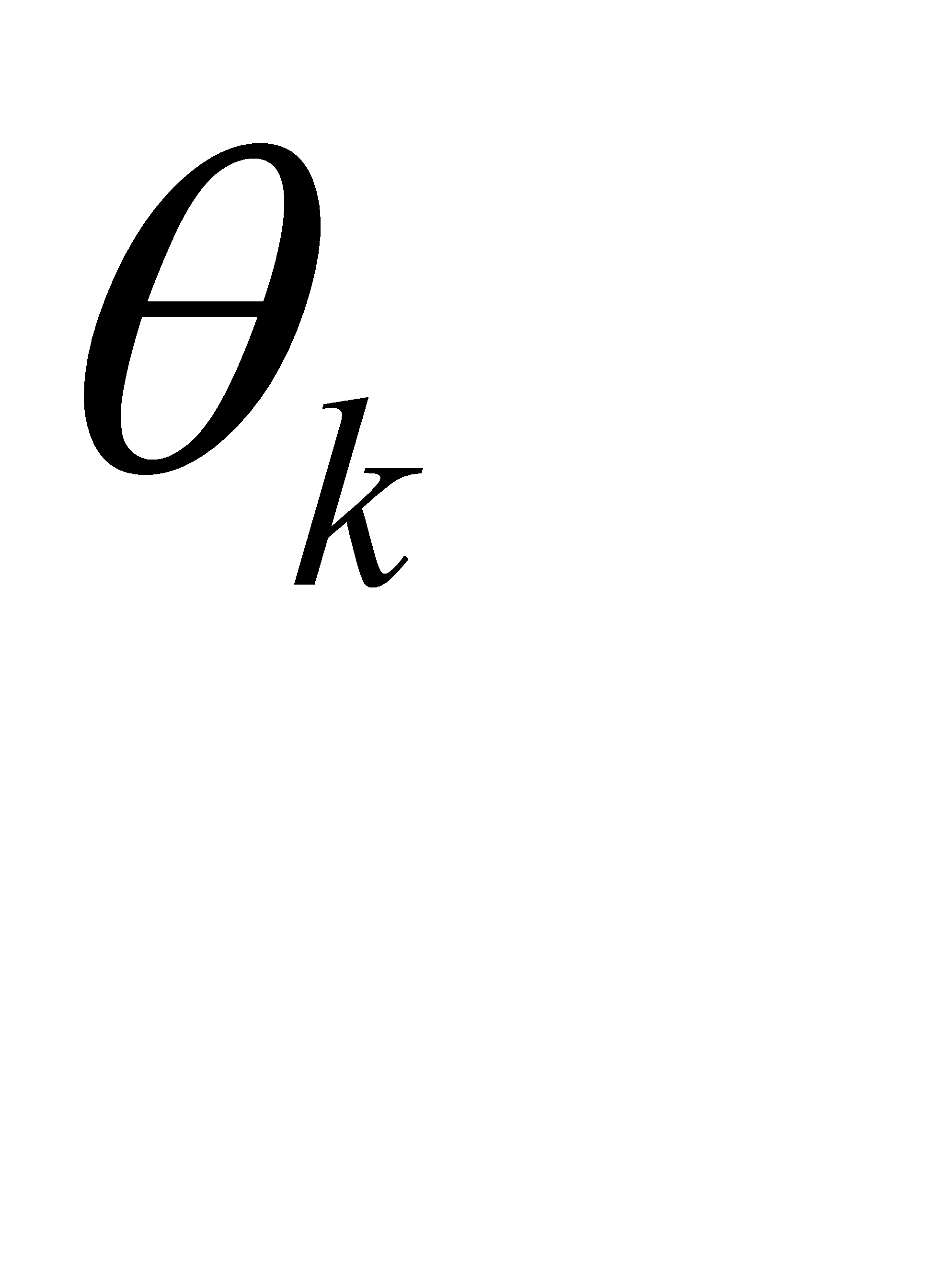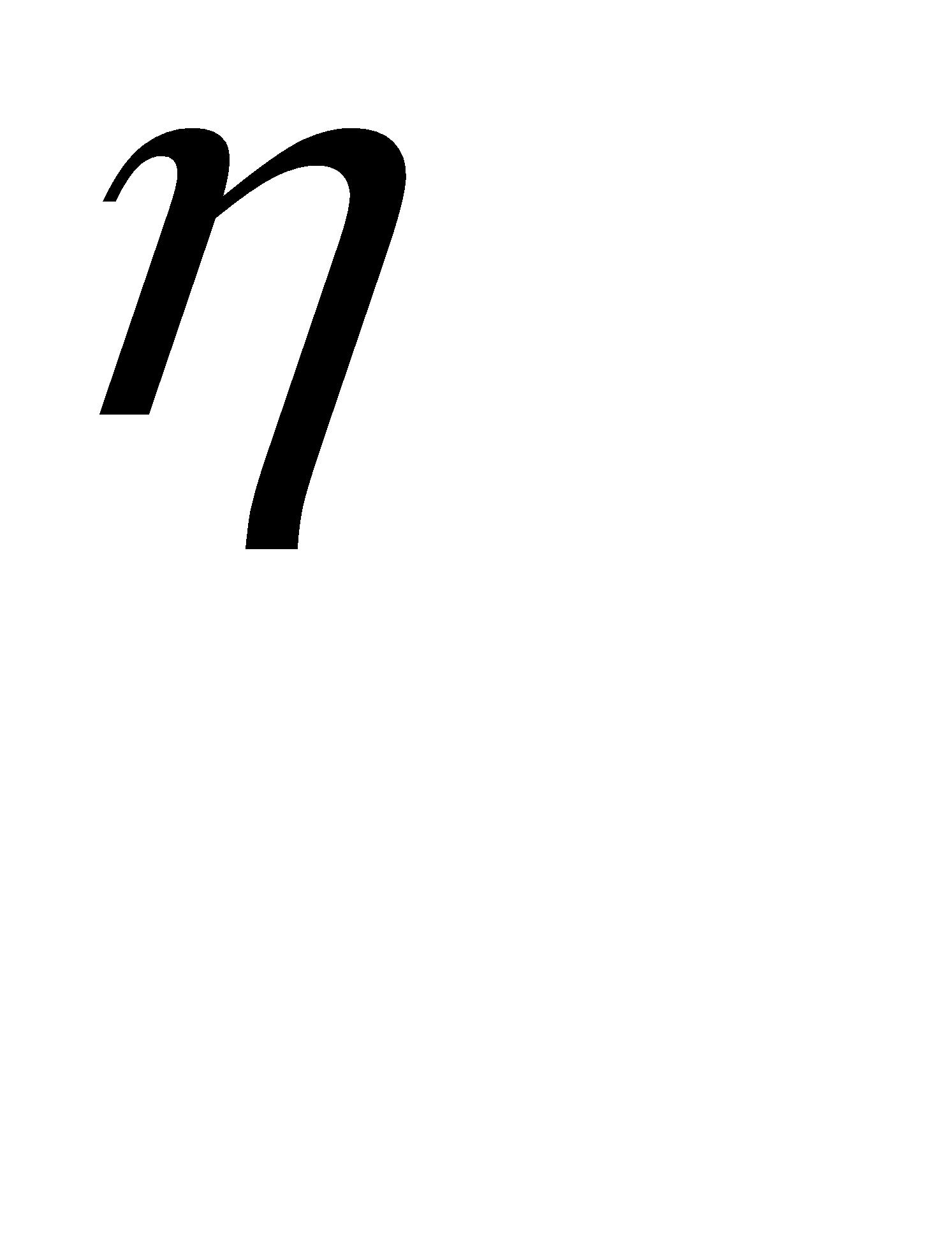и 
.
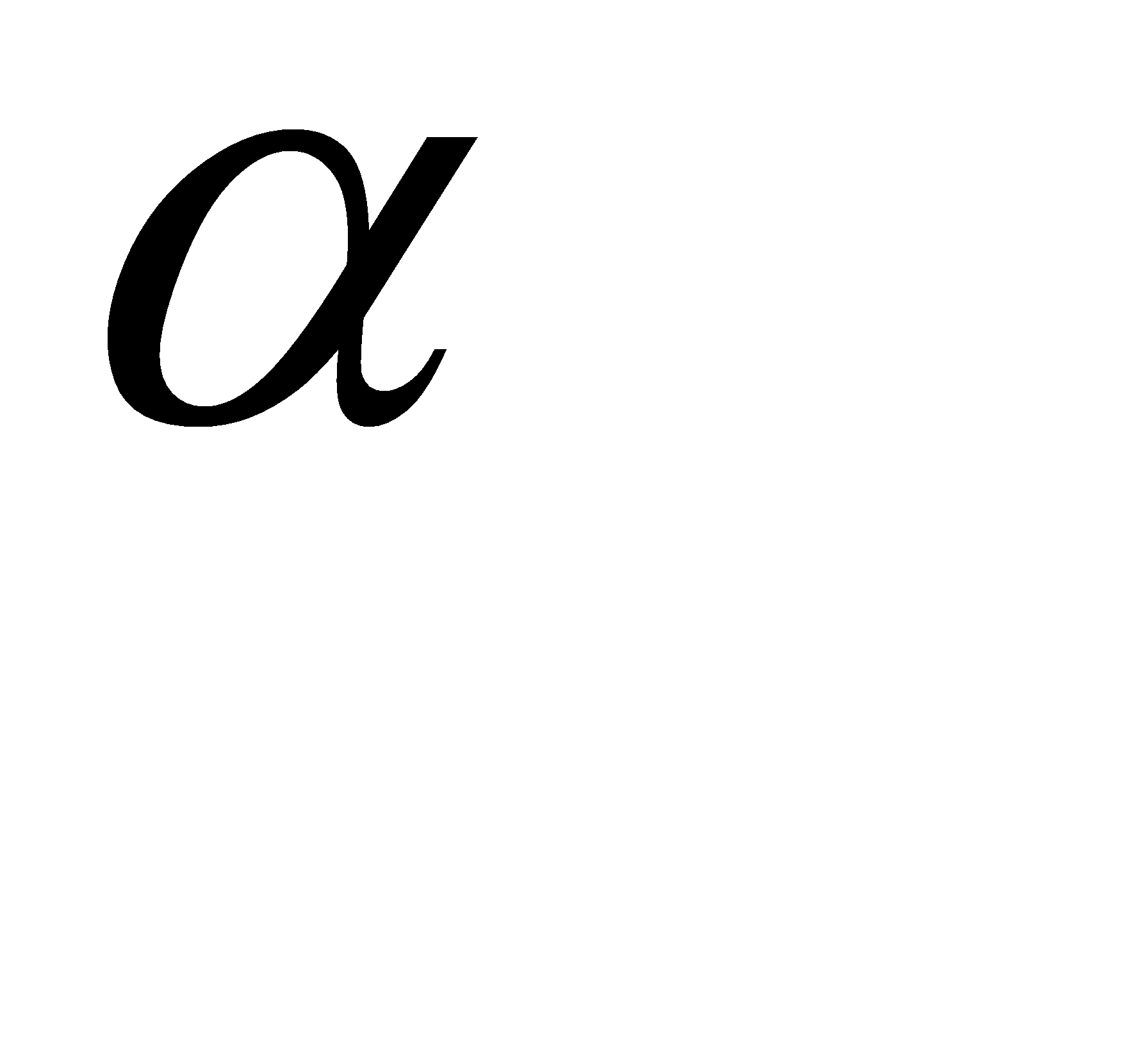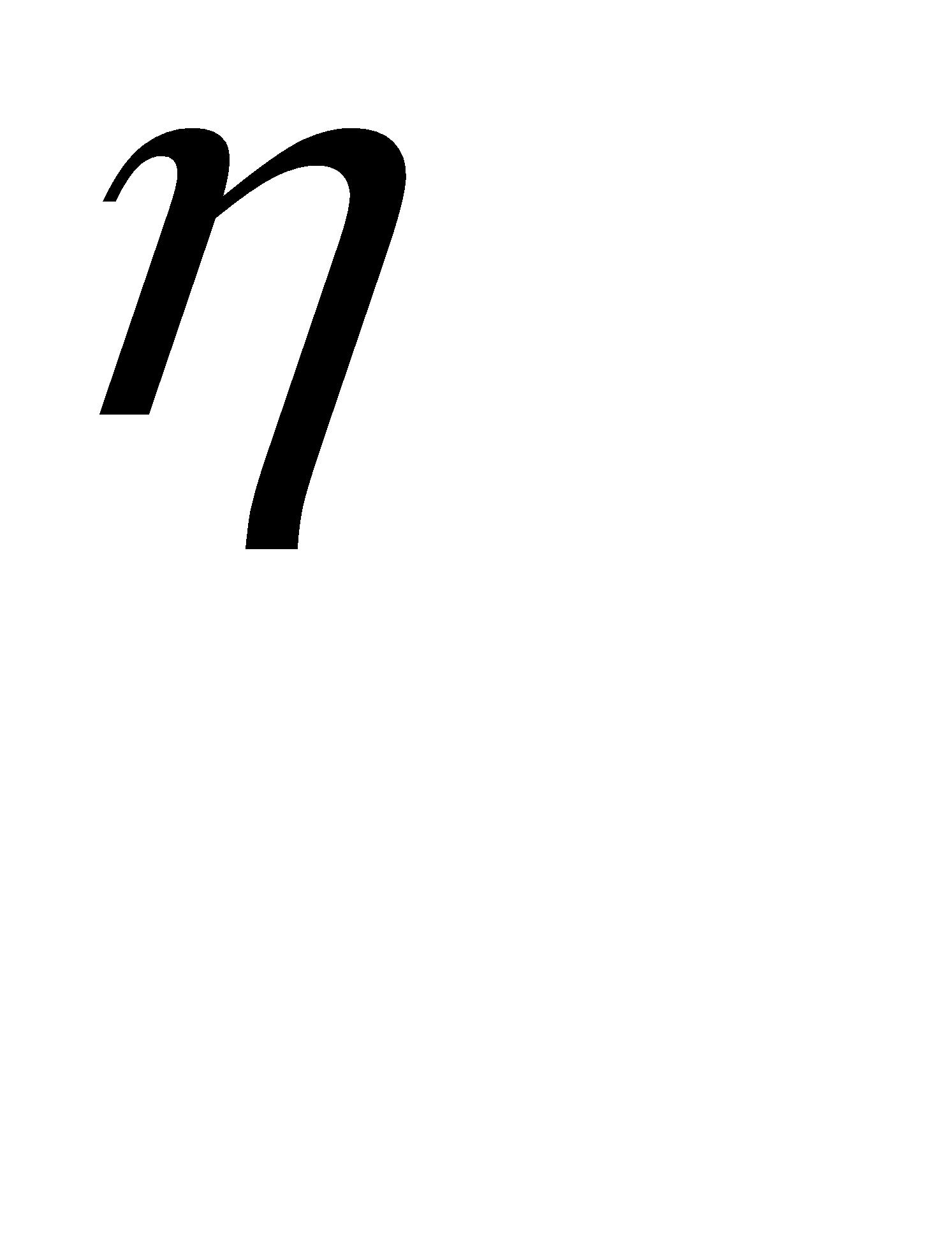— это скорость обучения, 
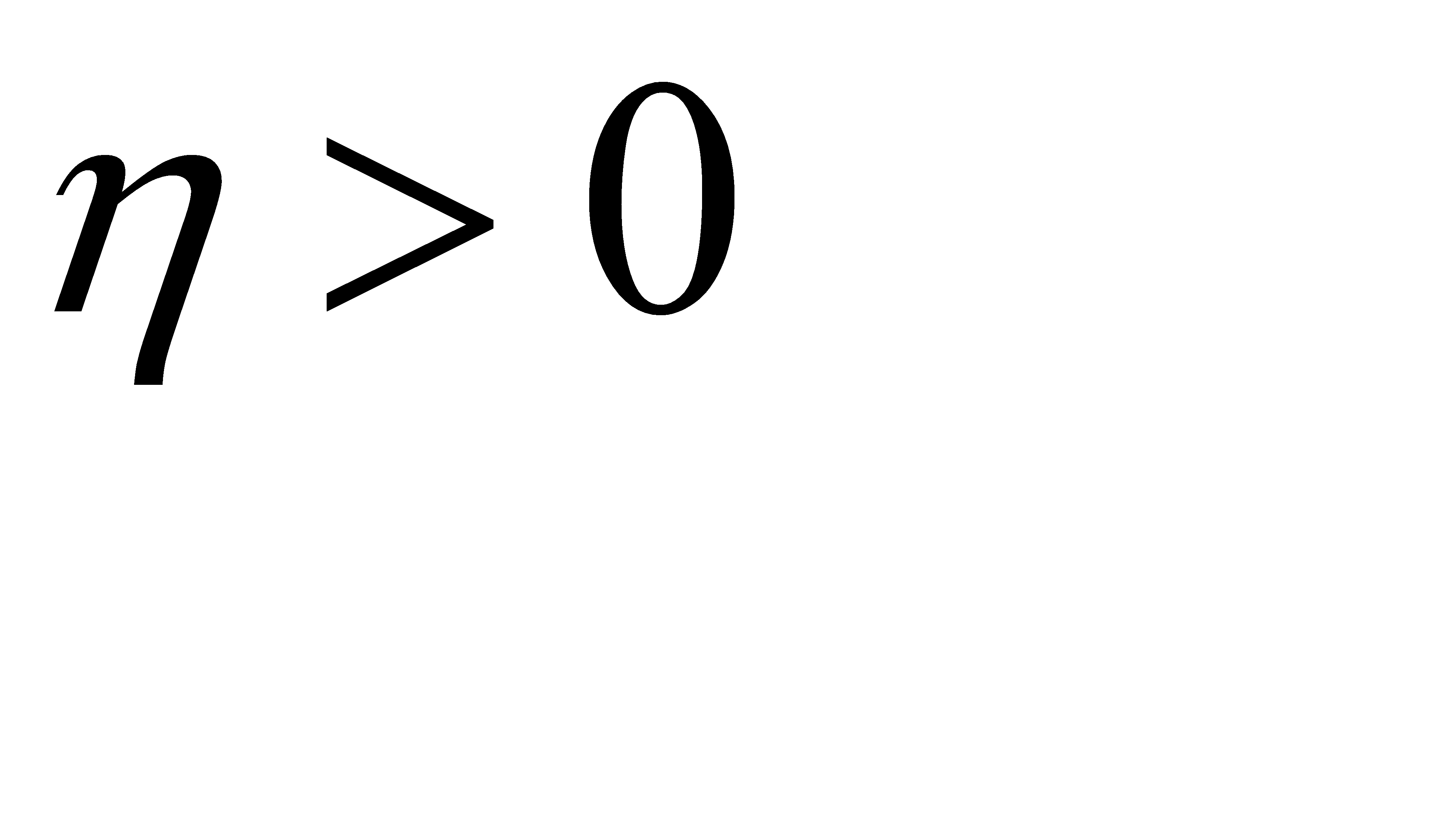; Это константа, представляющая собой коэффициент пропорциональности между изменением веса связи и градиентом ошибки E относительно веса. Чем больше эта константа, тем больше изменения в весах связей.
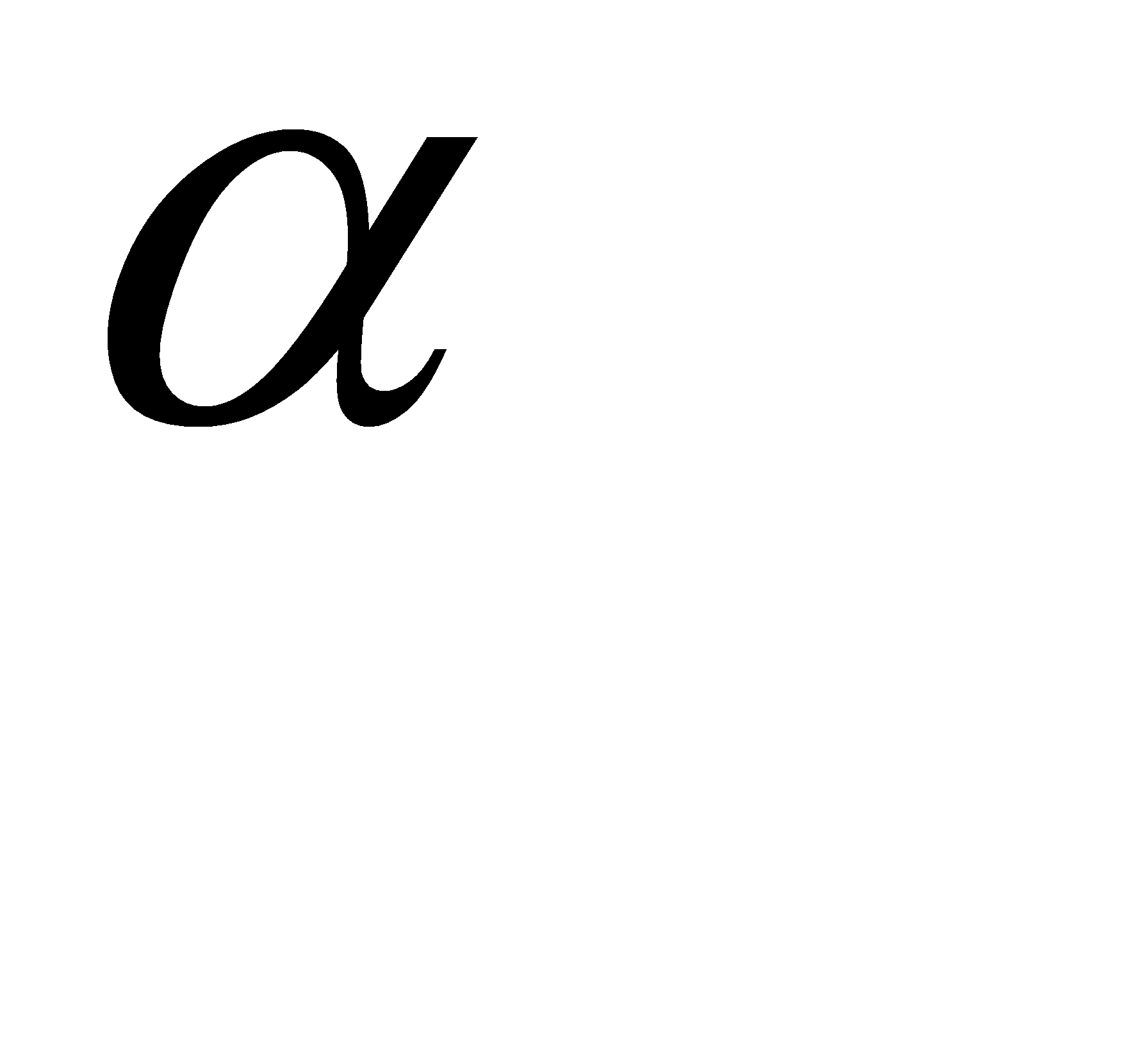— константа, определяющая влияние предыдущего изменения весов на текущее направление движения в пространстве весов связей. Учёный с мировым именем Румельхарт рекомендует использовать величину альфа, приблизительно равную 0,9.
Шаг 2. Подать на нейронную сеть входной сигнал. Задать соответствующий ему желаемый выход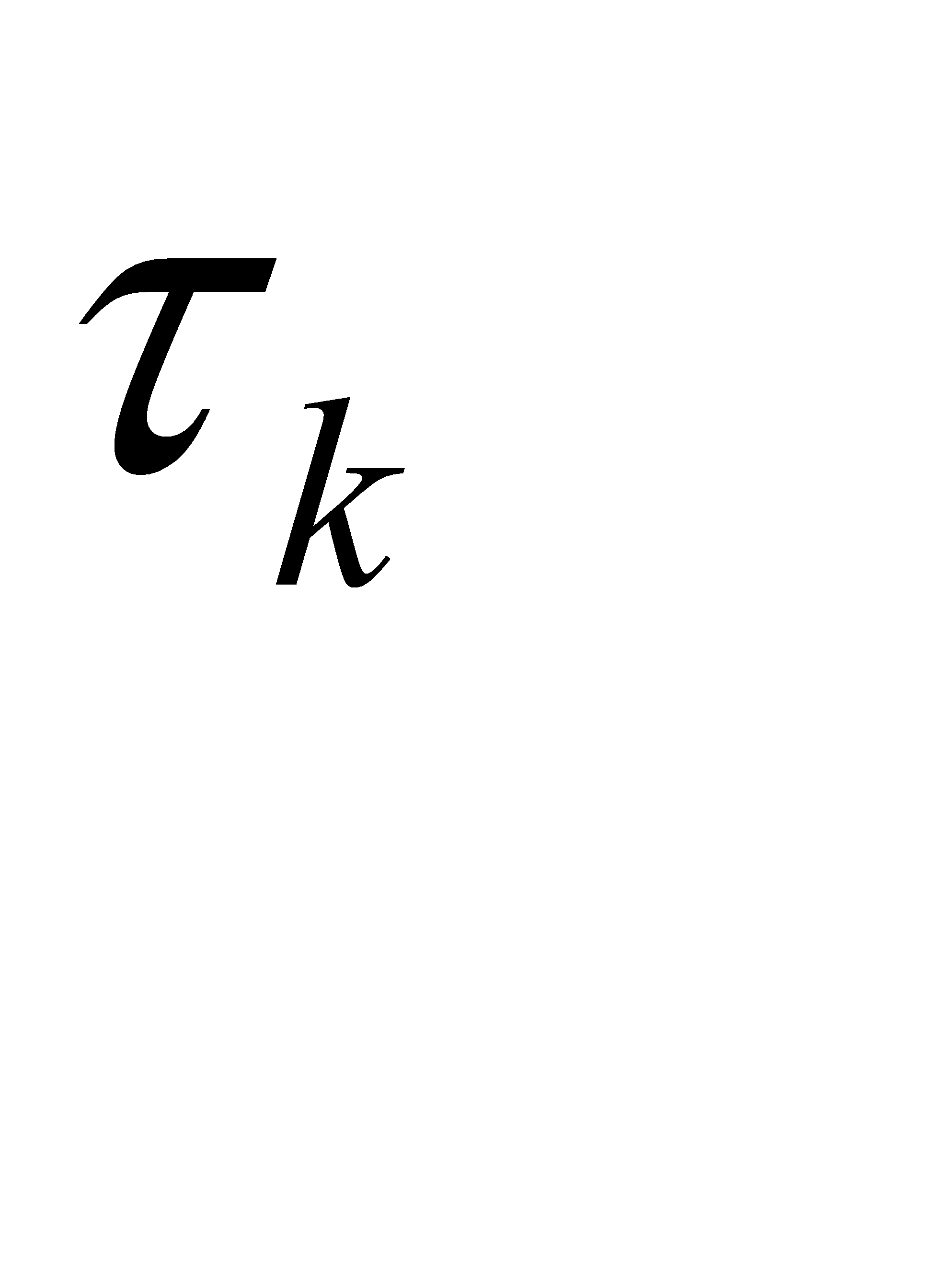 
, вычислить 
, 
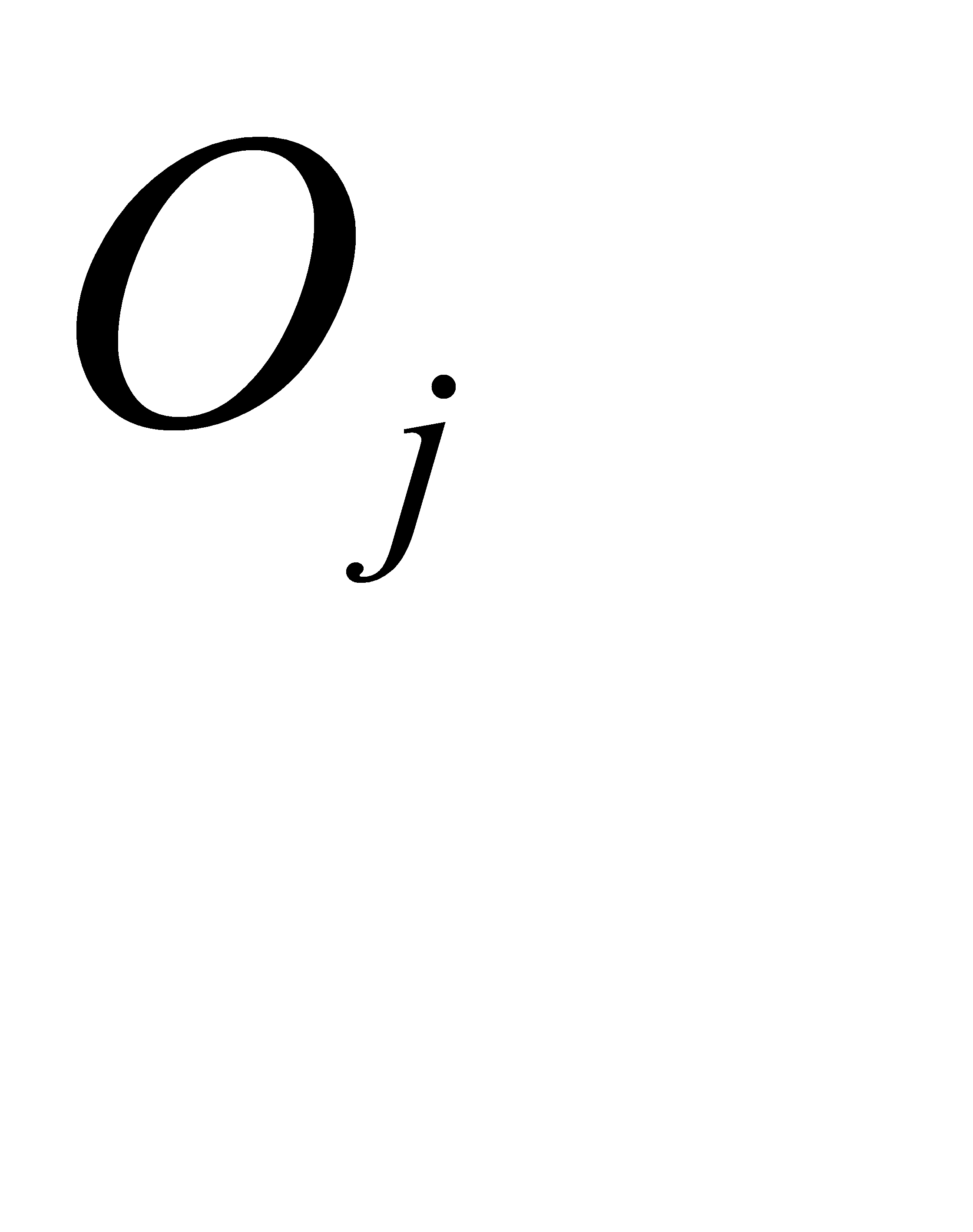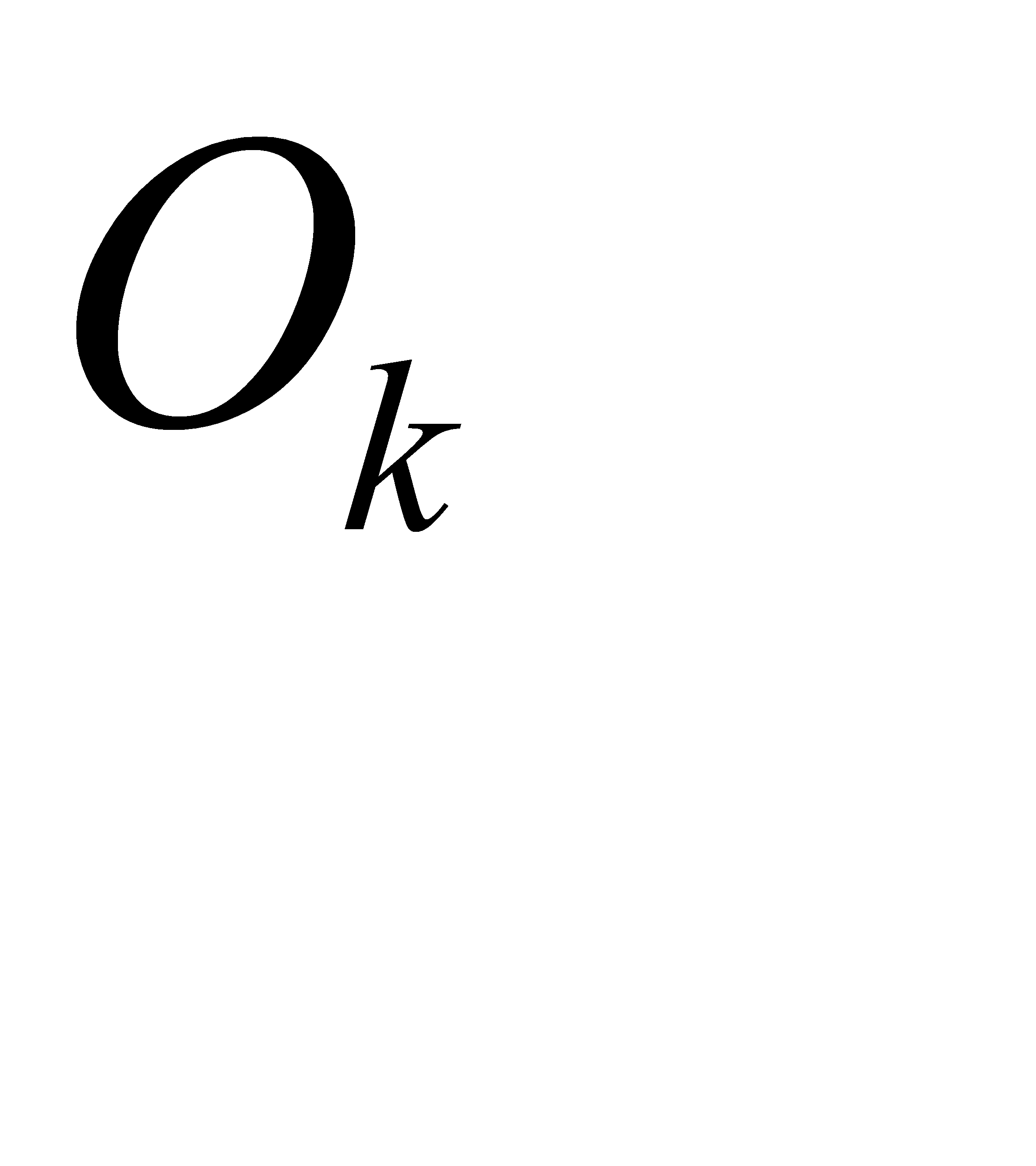и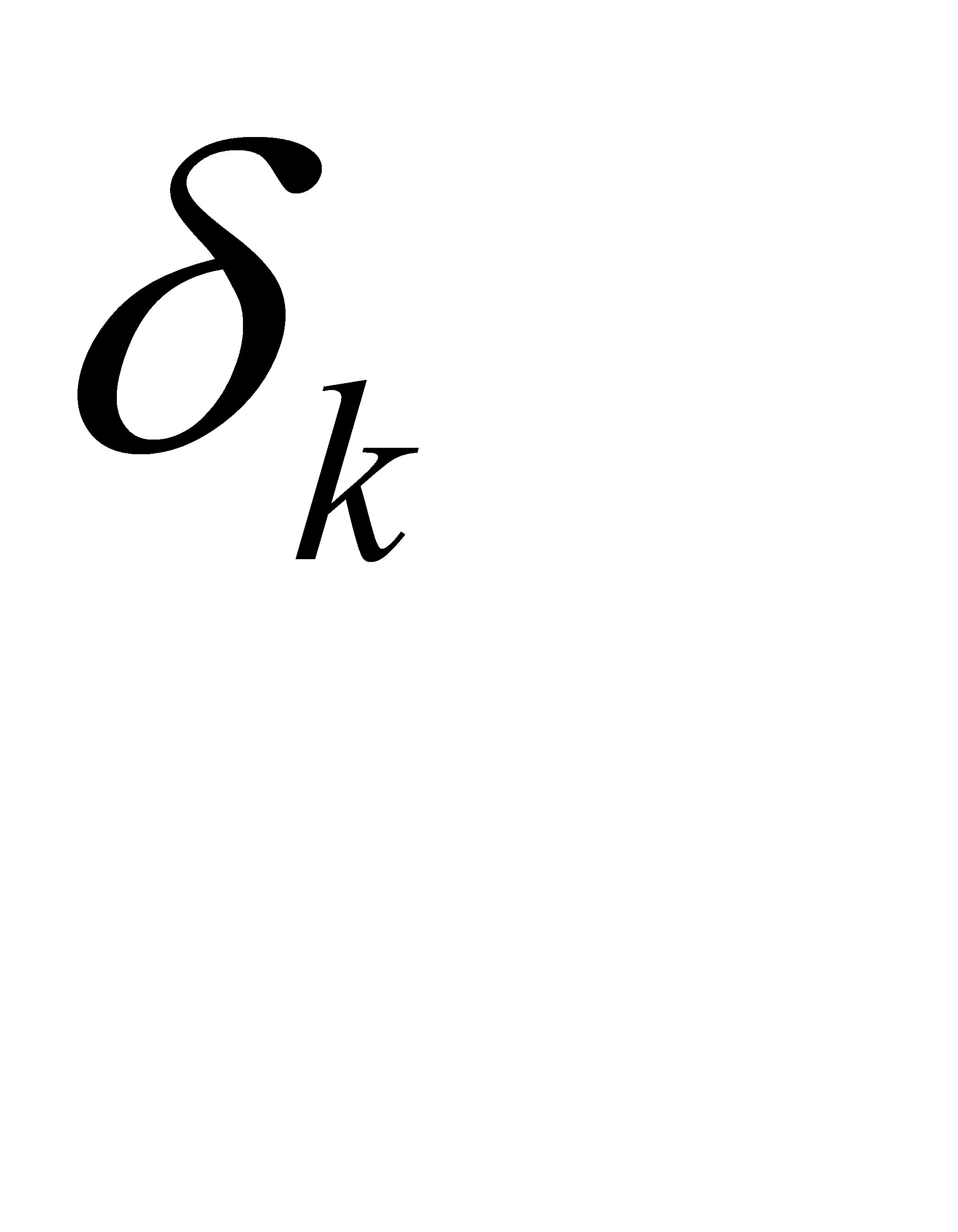 
по формуле:
.
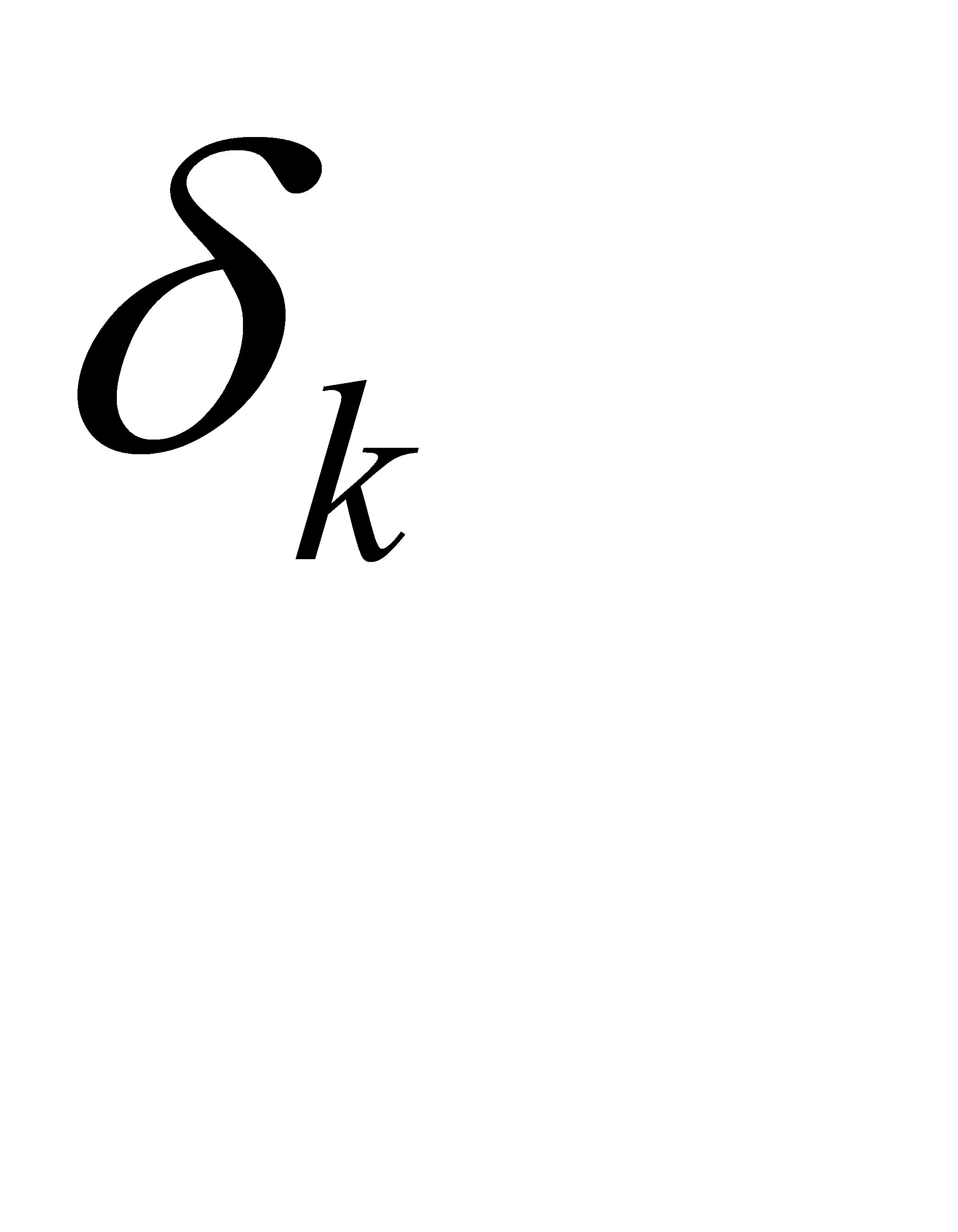— это величина обобщённого сигнала ошибки, задаваемая выражением:
.
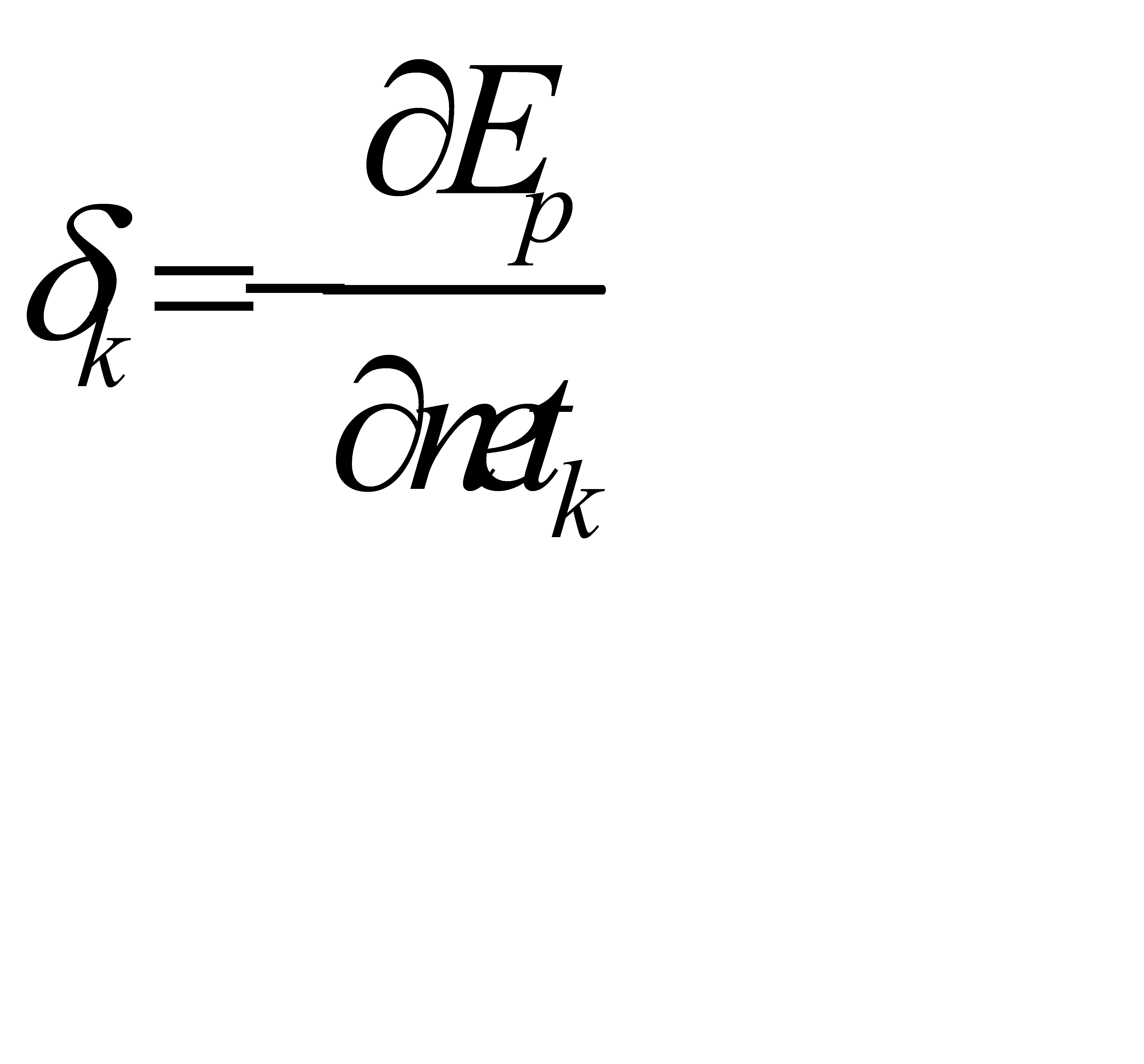Шаг 3. Изменить веса связей на величину:
.
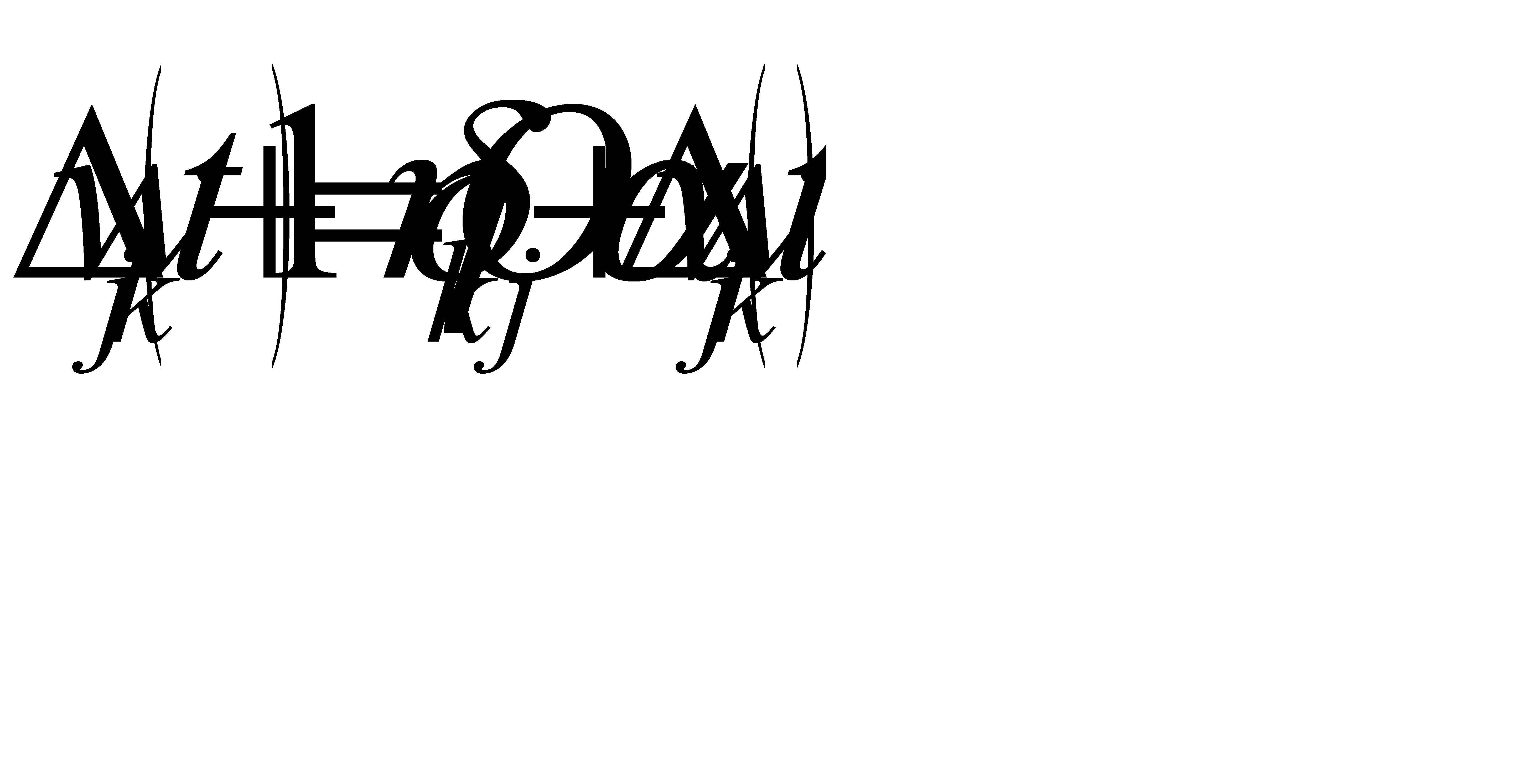Шаг 4. Вычислить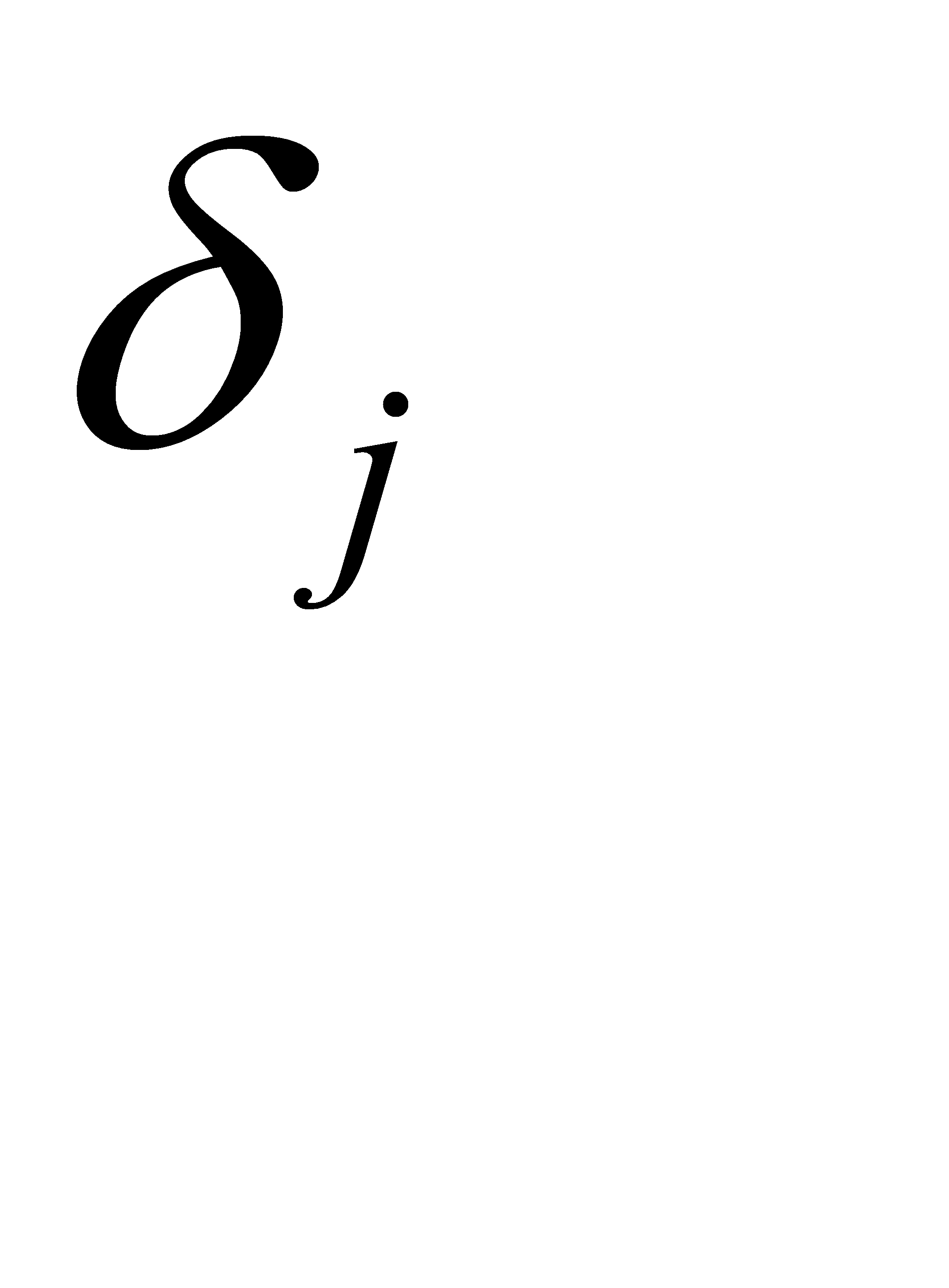 
по формуле:
.
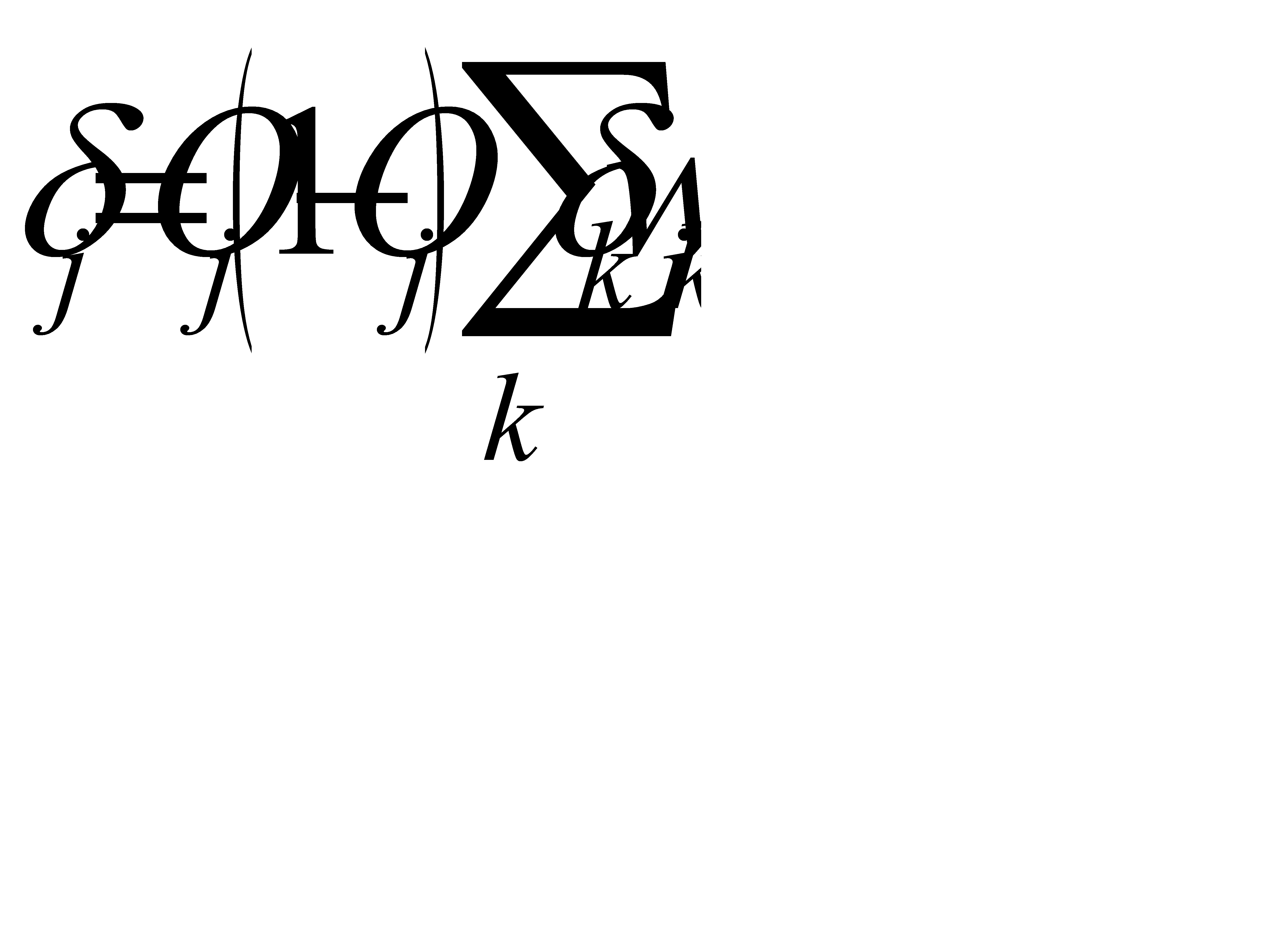Шаг 5. Изменить веса связей на величину:
.
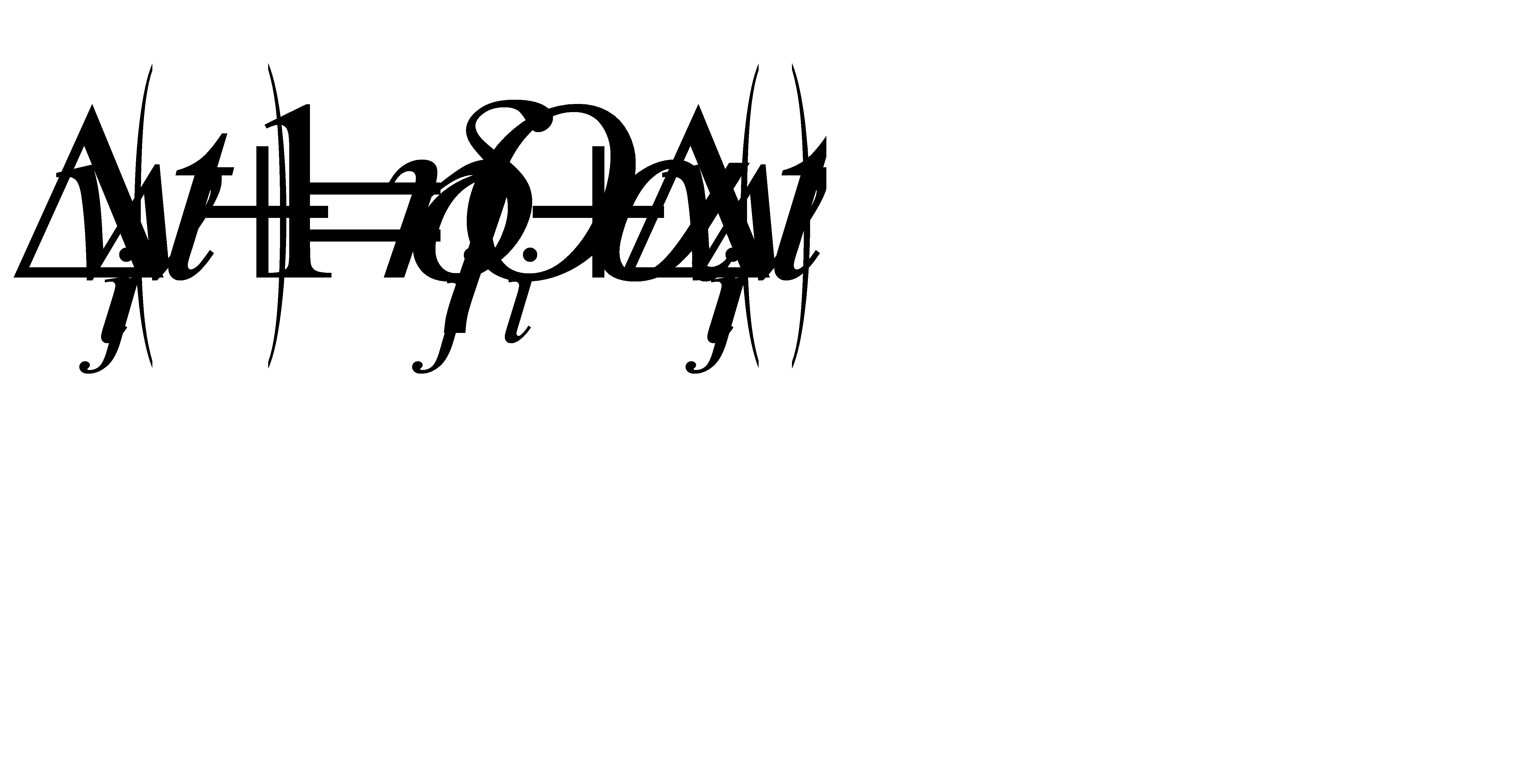Шаг 6. Положить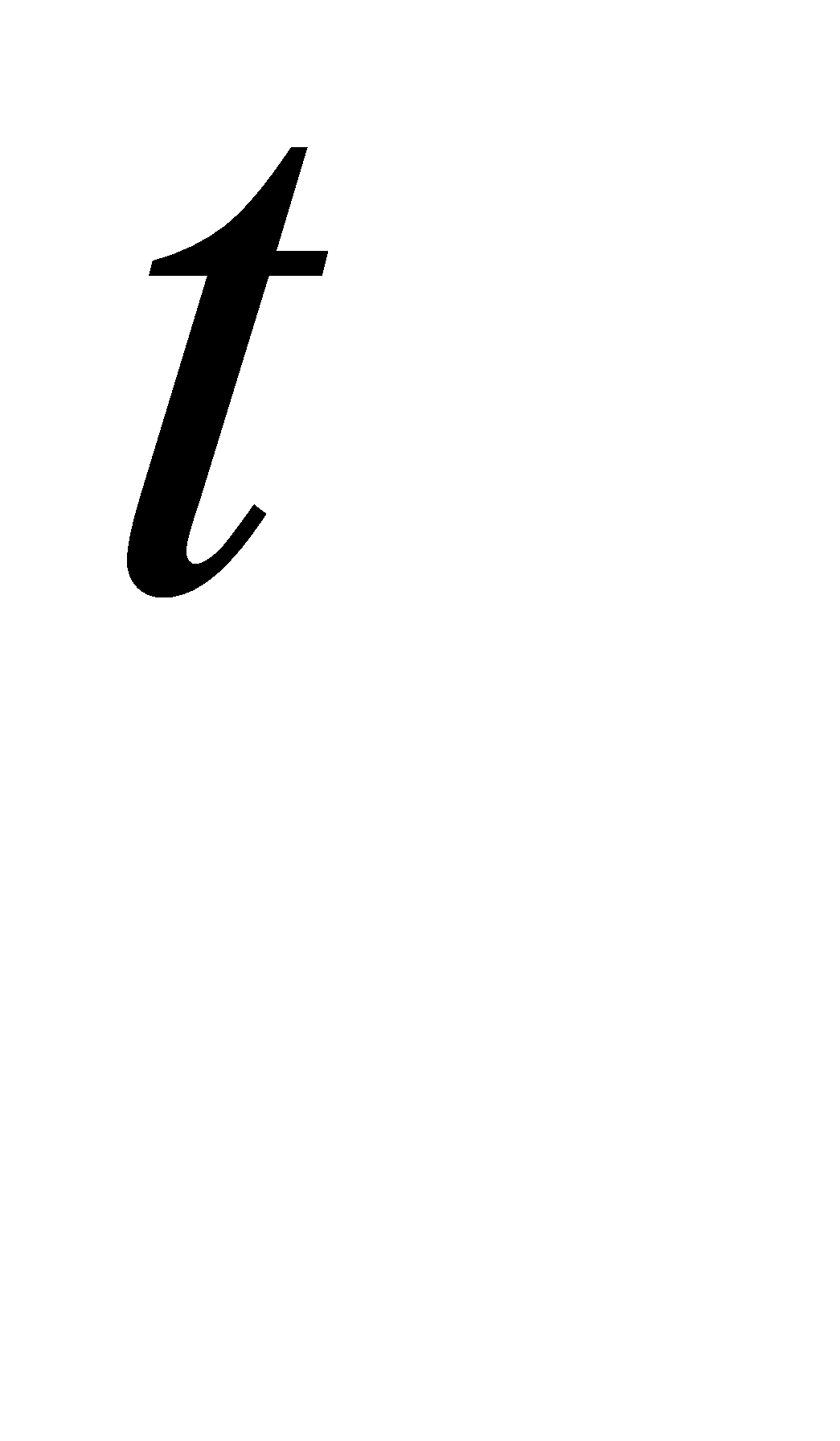 
равным 
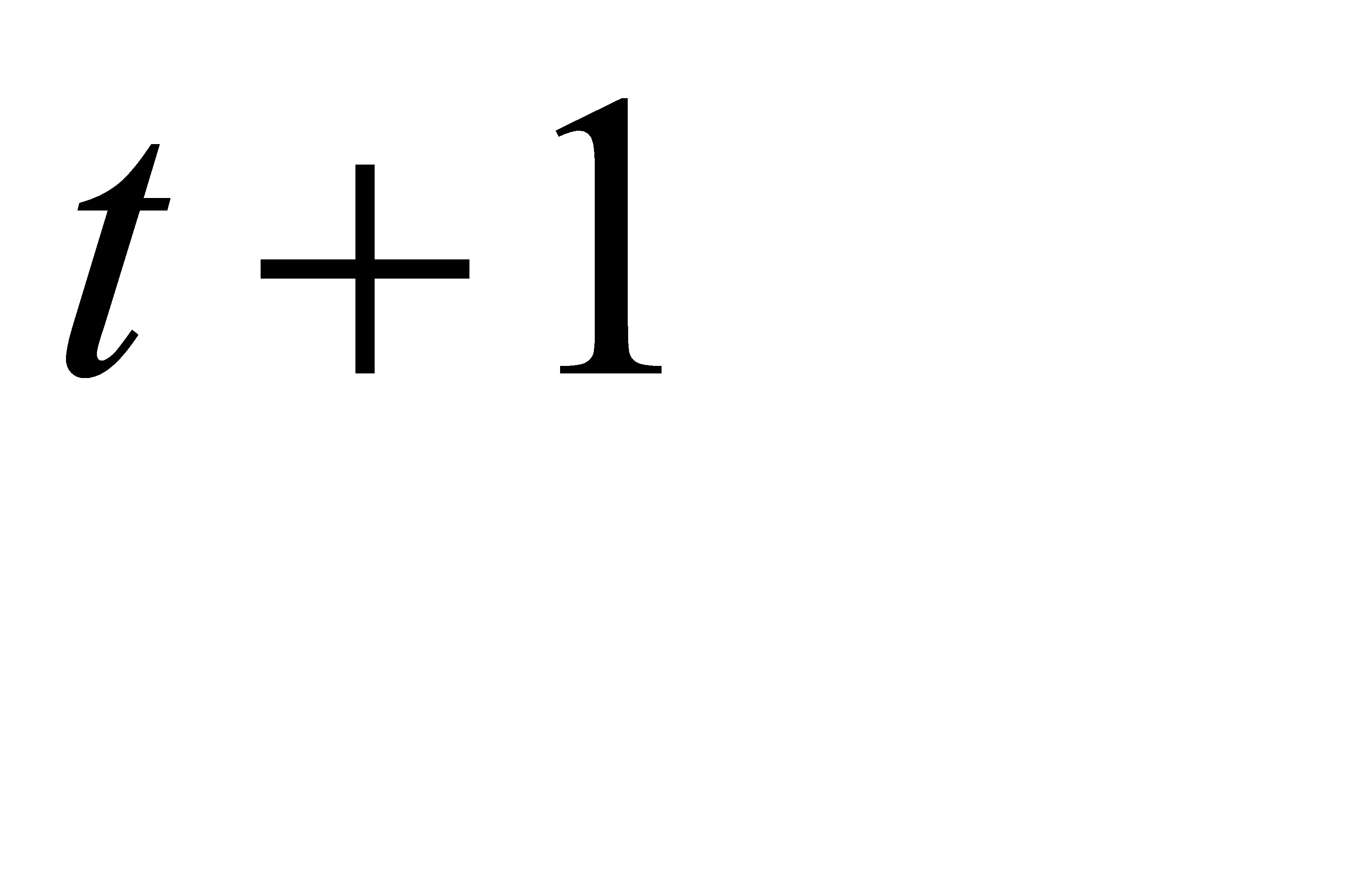и перейти к шагу 2.
Недостатки алгоритма
Паралич сети
В процессе обучения сети значения весов могут в результате коррекции стать очень большими величинами. Это может привести к тому, что все или большинство нейронов будут функционировать при очень больших значениях OUT, в области, где производная сжимающей функции очень мала.
Локальные минимумы
Алгоритм обратного распространения получен на основе градиентного метода наискорейшего спуска и предназначен для поиска минимума ошибки. Это приводит, однако, к поиску локального минимума или точки перегиба. В идеальном же случае должен отыскиваться глобальный минимум, представляющий собой нижнюю точку всей области определения.
Размер шага
Размер шага должен браться конечным. Если размер шага фиксирован и очень мал, то сходимость слишком медленная, если же он фиксирован и слишком велик, то может возникнуть паралич или постоянная неустойчивость.