Для примера рассмотрим 10-е положение механизма.
Средняя угловая скорость начального звена ОА
где n – частота вращения кривошипа ОА
Скорость точки А находим по формуле
VA=w*lOA *Ks = 10.47*0.04*2=0.838м/с
При этом 
Принимаем длину отрезка (pva), изображающего скорость VA точки А, равной 83.8мм.
Тогда масштабный коэффициент плана аналогов скоростей
Рассматривая движение точки В вместе с точками А и С (переносное движение) и относительно этих точек, получим векторные уравнения для построения скорости точки:
.
Величина скорости точки В
Скорость точки D определяем по принципу подобия:
[рb]/ [рd]=CВ/СD
[рd]= [рb]· СD/ CВ
[рd]=210 мм
VD=210·0,01=2,1 м/с.
4. Звено 4 совершает сложное движение, состоящее из вращательного вокруг точки E и поступательного вдоль направляющей XX.
Решаем это уравнение построением плана скоростей.
Проводим из точки D направление вектора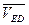 
, перпендикулярно звену ED. Из точки р – полюса плана скоростей проводим прямую параллельно XX. Точку пересечения обозначим точкой E.
Определяем искомые скорости:
VE = [рe]×Kv = 204×0.01 = 2.04 м/с; VED = [de]×Kv = 40×0.01 = 0,4 м/с.
Определим угловую скорость звеньев:
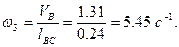(6)
(7)
Определение ускорений точек звеньев механизма
Ведем расчет для 10-го положения.
Построение плана ускорений начинаем с точки А звена ОА. Абсолютное ускорение определяется из выражения:
 .
|
Здесь нормальная составляющая направлена вдоль звена ОА к центру вращения (точке О) и равна по величине (для десятого положения):
 ,
| ||
Тангенциальная составляющая равна 0, так как w1=const и  :
| ||
Второе звено совершает сложное движение, состоящее из вращательного относительно третьего звена и вращательного относительно первого звена. Составляем векторное уравнение для структурной группы 2-3:
В этом уравнении величины ускорений равны:
;
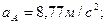
Примем масштабный коэффициент Ka = 0,05 м/с2×мм.
Из произвольной точки P – полюса плана ускорений, проводим вектор Pа параллельно звену ОА в направлении от точки А к точке О. Величина отрезка равна:
.
Конец вектора обозначаем точкой а.
Из точки a в направлении от точки В к точке А параллельно АB проводим вектор нормальной составляющей 
, конец вектора обозначаем буквой n1. Величина отрезка равна:
.
Из точки n1 проводим линию перпендикулярную звену АB.
Из полюса P проводим вектор ускорения 
. Направление ускорения параллельно звену ВС. Ускорение определяется отрезком:
.
Из точки n2 проводим линию перпендикулярную звену BC до пересечения с линией проведенной из точки n1. Точку пересечения обозначаем точкой b.
Определяем величины ускорений:
= [Pb]×Kа = 146×0,05 = 7,3 м/с2;
= [n1b]×Kа = 288×0,05 = 14,4 м/с2;
= [ab]×mа = 299×0,05 = 14,95 м/с2;
= [bn2]×mа = 28×0,05 = 1,4 м/с2.
Определяем величину углового ускорения 2-го и 3-го звена:
 .
|
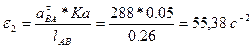Ускорение точки D найдем по теореме подобия.
[рb]/ [рd]=CВ/СD
[рd]= [рb]· СD/ CВ
[рd]=146*0.24/0,34=233,6 мм
aD=82,9∙0,05=11.68 м/с.
Составляем векторное уравнение для структурной группы 4-5:
 ,
|
где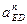 
- нормальное ускорение точки E во вращательном движении ползуна относительно точки D; 
- тангенциальное ускорение точки E во вращательном движении ползуна относительно точки D.
.
Из точки D параллельно ED проводим вектор ускорения аEDn.
[dn3]=1.9/0,05=38 мм
Из конца вектора проводим прямую, перпендикулярную ED, которая будет характеризовать тангенциальное ускорение точки Е. 
Из полюса параллельно XX проводим вектор ускорения аEn. В точке пересечения этих прямых ставим точку е.
Определим величины ускорений:
= [n3e]×Kа = 232,28×0,05 = 11,61 м/с2;
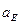= [Pe]×Kа = 29×0,05 = 1.45 м/с2;
= [PS1]×Kа = 88×0,05 = 4,385 м/с2
= [PS2]×Kа = 61×0,05 = 2,295 м/с2.
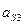=[PS3]×Kа =117∙0.05=5.3 м/с2
= [PS4]×mа = 118×0,05 = 5,644 м/с2
Определяем величину углового ускорения четвертого звена:
.
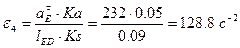