Описание II алгоритма
Второй алгоритм (или метод обратной матрицы) симплекс метода основан на ином способе вычисления оценок 
векторов условий Аj, чем в первом алгоритме.
Рассматривается задача линейного программирования в канонической форме (2.1) - (2.3). Пусть Х – опорный план с базисом 
. Все параметры, необходимые для оценки плана на оптимальность и перехода к лучшему плану, можно получить, преобразовывая от шага к шагу элементы матрицы 
.
Действительно, зная обратную матрицу 
, можно получить базисные составляющие опорного плана:
и вычислить оценки векторов условий относительно текущего базиса
, (6.1)
предварительно определив вектор-строку 
по формуле
или
. (6.2)
Здесь 
- вектор-строка из коэффициентов линейной формы, отвечающих базисным переменным.
Оценки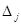 
позволяют установить оптимальность рассматриваемого опорного плана и определить вектор Ак, вводимый в базис. Коэффициенты 
разложения вектора Ак по текущему базису вычисляются по формуле
.
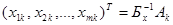Как и в I алгоритме, вектор, подлежащий исключению из базиса, определяется величиной
.
Таким образом при втором алгоритме на каждом шаге запоминаются базисные компоненты 
, обратная матрица , значение линейной формы F(X) и вектор Y, соответствующие текущему опорному плану Х. Элементы столбцов матрицы удобно рассматривать как коэффициенты 
разложения единичных векторов 
по векторам базиса. Рекуррентные формулы, связывающие параметры двух последовательных итераций
; (6.3)
. (6.3)
Здесь
.
Результаты вычислений сводятся в основные таблицы (вида табл. 6.1) и вспомогательную таблицу (вида табл. 6.2); столбцы В, е1, …, еm основных таблиц (все m +1 позиций) называют главной частью этих таблиц. Столбец Аk – разрешающий столбец, строка l – разрешающая строка.
Таблица 6.1 Таблица 6.2
| N |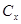 
| 
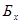
| B | 
| … | 
| 
| t | N | B | 
| 
| … | 
| |
| 
| 
| 
| … | 
| 
| 
| 
| 
| … | 
| ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
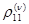
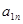
| l | 
| 
| 
| 
| … | 
| 
| 
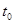
| m | 
| 
| 
| … | 
| |
|
|
|
|
|
|
|
|
|
| m +1 | C | 
| 
| … | 
| |
| M |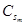 
| 
| 
| 
| … | 
| 
| 
| 
| 
| … | 
| |||
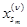
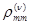
| m +1 | – | – |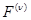 
| 
| … | 
| 
| – | 
| 
| 
| … | 
| ||
| 
| 
| … | 
| |||||||||||
| … | … | … | … | … | … |
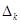
Краткое описание алгоритма.
1. Нулевая итерация:
а) составляется вспомогательная табл. 6.2, в которую вносятся параметры задачи; дополнительная строка таблицы с номером ν заполняется по мере выполнения ν -й итерации;
б) составляется основная табл. 6.1 с номером 0, в которой заполняются первые m строк, за исключением последних двух столбцов Аk и t. Элементы 
и 
определяются скалярными произведениями (Cx, ej) и (Cx, B) соответственно. Нулевая итерация заканчивается заполнением нулевой дополнительной строки вспомогательной таблицы с оценками 
.
2. (ν +1)-я итерация.
Пусть ν -я итерация закончена. В результате заполнена ν -я основная таблица, за исключением двух последних столбцов, и ν -я дополнительная строка вспомогательной таблицы. Просматривается эта строка. Если все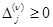 
, то опорный план 
- решение задачи. Если хотя бы одна 
, то в базис вводится вектор Аk с 
(обычно 
). После этого заполняется столбец 
основной таблицы. В позицию (m +1) этого столбца заносится оценка 
вектора Аk. Остальные элементы этого столбца равны
.
Возможны два случая:
1) все 
- задача неразрешима;
2) 
хотя бы для одного i. В этом случае, также как и в первом алгоритме, заполняется столбец (t) основной таблицы ν, определяется разрешающий элемент 
. Главная часть заполняется по рекуррентной формуле (6.3). Заполняется (ν +1)-я дополнительная строка вспомогательной таблицы. На этом заканчивается (ν +1)-я итерация.
Решение М-задачи
Таблица 6.3
Таблица 6.4
Задача (5.4), (5.5) имеет опорный план Х0 = (0, 0, 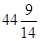0, 
, 
, 
, 
, 0, 
) с базисом 
. Следовательно, 
. Процесс решения М-задачи вторым алгоритмом приведен в основной табл. 6.3 и вспомогательной табл. 6.4.
Решение М-задачи получено за 5 шагов. Оптимальный план ее равен 
и 
. В оптимальном плане М-задачи искусственная переменная х9 = 0, поэтому 
- решение задачи (2.12), (2.13) и 
.
Окончательное решение задачи определения плана смешения компонентов полностью повторяет решение, рассмотренное в завершающей части п.4 (см. стр.11-12).