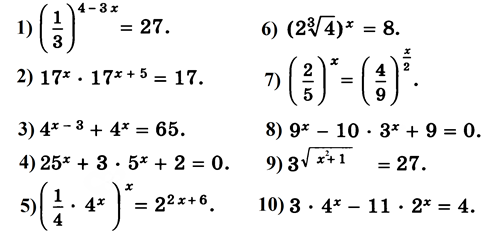Самостоятельная работа №2 : «Решение показательных уравнений»

Тема: «Решение показательных уравнений»

СР.№1 «Показательные уравнения»

Вариант 1

1. Найдите корень уравнения .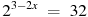

2. Найдите корень уравнения .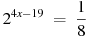

3. Найдите корень уравнения .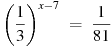

4. Найдите корень уравнения: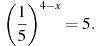

5. Найдите корень уравнения .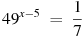

6. Найдите корень уравнения .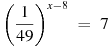

7. Найдите корень уравнения: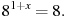

8. Найдите корень уравнения: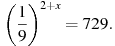

9. Найдите решение уравнения: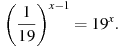

10. Решите уравнение .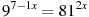

11. Решите уравнение .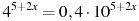

СР.№1 «Показательные уравнения»

Вариант 2.

1. Найдите корень уравнения .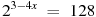

2. Найдите корень уравнения .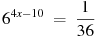

3. Найдите корень уравнения .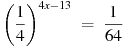

4. Найдите корень уравнения: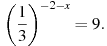

5. Найдите корень уравнения .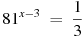

6. Найдите корень уравнения .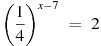

7. Найдите корень уравнения: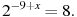

8. Найдите корень уравнения: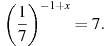

9. Найдите решение уравнения: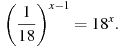

10. Решите уравнение .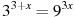

11. Решите уравнение .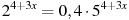

СР.№1 «Показательные уравнения»

Вариант 3.

1. Найдите корень уравнения .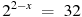

2. Найдите корень уравнения .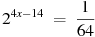

3. Найдите корень уравнения .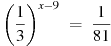

4. Найдите корень уравнения: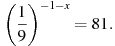

5. Найдите корень уравнения .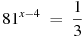

6. Найдите корень уравнения .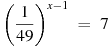

7. Найдите корень уравнения: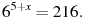

8. Найдите корень уравнения: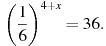

9. Найдите решение уравнения: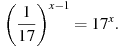

10. Решите уравнение .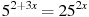

11. Решите уравнение .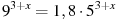

СР.№1 «Показательные уравнения»

Вариант 4.

1. Найдите корень уравнения .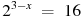

2. Найдите корень уравнения .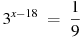

3. Найдите корень уравнения .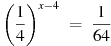

4. Найдите корень уравнения: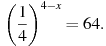

5. Найдите корень уравнения .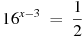

6. Найдите корень уравнения .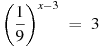

7. Найдите корень уравнения: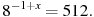

8. Найдите корень уравнения: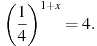

9. Найдите решение уравнения: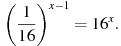

10. Решите уравнение .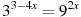

11. Решите уравнение .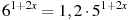

СР.№1 «Показательные уравнения»

вариант5.

1. Найдите корень уравнения .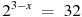

2. Найдите корень уравнения .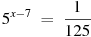

3. Найдите корень уравнения .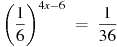

4. Найдите корень уравнения: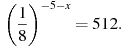

5. Найдите корень уравнения .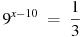

6. Найдите корень уравнения .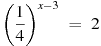

7. Найдите корень уравнения: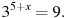

8. Найдите корень уравнения: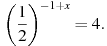

9. Найдите решение уравнения: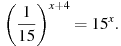

10. Решите уравнение .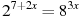

11. Решите уравнение .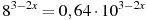

 

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ

ПРАКТИЧЕСКОЙ РАБОТЫ№ 13

Учебная дисциплина: Математика (включая алгебру и начала математического анализа, геометрию).

Тема: «Решение показательных уравнений различными методами».

Цель занятия: Обобщить и систематизировать знания по теме «Показательные уравнения, и методы их решений»; закрепить умения использовать полученные знания при решении показательных уравнений разными методами.

Норма времени: 80 мин.

Контрольные вопросы.

1. Какие уравнения называются показательными.

2. Основные свойства степени с рациональным показателем.

3. Основные свойства степени с действительным показателем.

Примеры и последовательность выполнения заданий

Методы решения показательных уравнений

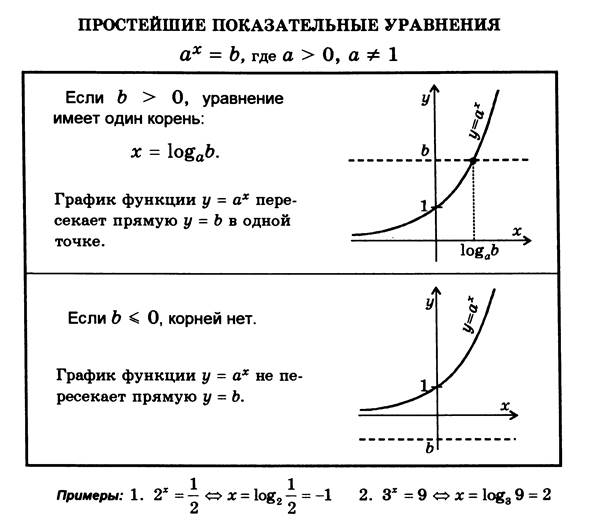
Простейшие показательные уравнения

Примеры.

Пример 1. Решите уравнение: 3^4x-5 = 3^x+4 .

Решение.

3^4x-5 = 3^x+4

4x -5 = x+4

3x=9

x = 3.

Ответ:3

Методы преобразования показательных уравнений к простейшим.

A. Метод уравнивания оснований.

Примеры.

Пример 1. Решите уравнение: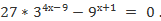

Решение.

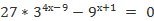
3³3^4x-9- (3²)^x+1 = 0

3^{3+ (4x-9)}- 3^2(x+1) = 0

3^4x-6-3^2x+2 = 0

3^4x-6 = 3^2x+2

4x-6=2x+2

2x = 8

x=4. Ответ: 4.

Пример 2. Решите уравнение: .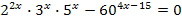

Решение.

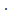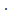(2²)^x 3^x 5^x - 60^4x-15 =0

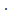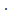(2²)^x 3^x 5^x = 60^4x-15

4^x 3^x 5^x = 60^4x-15

(4 3 5)^х= 60^4x-15

60^x=60^4x-15

x=4x-15

3x=15

x=5. Ответ: 5.

В. Уравнения, решаемые разложением на множители.

Примеры.

Пример 1. Решите уравнение: x 2^x = 2 2^x + 8x-16.

Решение.

x 2^x = 2 2^x + 8x-16

x 2^x - 2 2^x = 8 (x-2)

2^x (x-2) - 8 (х-2)

(x-2) (2^x - 8) = 0 <=> <=> <=> <=> .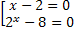

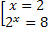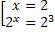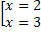Ответ: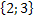

Пример 2. Решите уравнение: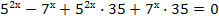

Решение.

5^2x - 7^x - 5^2x 35 +7^x 35= 0

(5^2x - 7^x)- (5^2x 35 +7^x 35)= 0

(5^2х-7^х)-35(5^2х-7^х)=0

(5^2х-7^х) 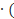1-35)=0

(5^2х-7^х) (-34)=0, т.к -34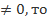

(5^2х-7^х)=0

(5²)^х=7^х

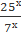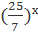⁼¹

=1

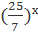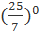= x=0 Ответ: 0.

С. Уравнения, которые с помощью подстановки 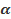^f(x) = t, t>0 преобразуются к квадратным уравнениям (или к уравнениям более высоких степеней).

Пусть 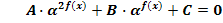, где А, В, С - некоторые числа. Сделаем замену: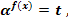 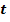>0, тогда A t² + B t + C = 0

Решаем полученное уравнение, находим значения t, учитываем условие t >0, возвращаемся к простейшему показательному уравнению 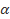^f(x) = t, решаем его и записываем ответ.

Примеры.

Пример 1. Решите уравнение: 2^2+x - 2^2-x = 15.

Решение.

2^2+x - 2^2-x =1 5

2²2^x - 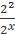= 15

4 (2^x)² - 4 = 15 2^x

Делаем замену t = 2^x, t > 0. Получаем уравнение 4t² - 4 = 15t <=> 4t² - 15t - 4=0

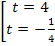<=> , t = 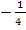не удовлетворяет условию t > 0.

Вернемся к переменной х:

2^х = 4

2^x = 2²

x=2. Ответ: 2

ВЫПОЛНИТЕ СЛЕДУЮЩИЕ ЗАДАНИЯ:

1 вариант 2 вариант

 

Решите уравнения:

1)

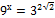
2)

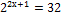
3)

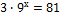
4)

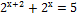
5)

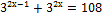
6)

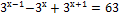
7)

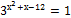
8)

 

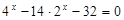
1)

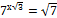
2)

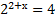
3) 2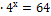

4)

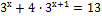
5)

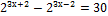
6)

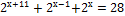
7)

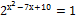
8)

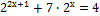
Самостоятельная работа №2: «Решение показательных уравнений»

ВАРИАНТ

 

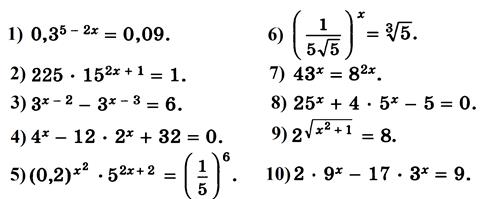
ВАРИАНТ