3. Две пружины с коэффициентами жёсткости k 1 и k 2 соединены последовательно.
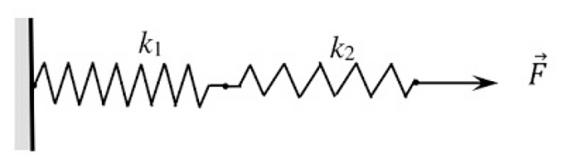
Чему равен коэффициент жёсткости k полученной таким образом составной пружины?
4. Две пружины с коэффициентами жёсткости k 1 и k 2, имеющие одинаковую длину в недеформированном состоянии, соединены параллельно.
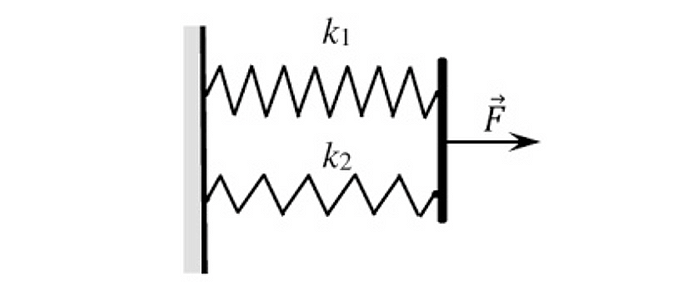
5. К ящику массой 15 кг, стоящему на горизонтальном полу, привязана лёгкая верёвка. Верёвку тянут с силой 40 Н в горизонтальном направлении. Чему равна сила трения, действующая на ящик со стороны пола, если коэффициент трения между полом и ящиком равен 0,3?
6. Пропускаем задачу
7. Найди ускорение свободного падения на планете Нептун, плотность которой в 3,4 раза меньше средней плотности Земли, а радиус в 3,9 раза больше земного радиуса.
Ускорение свободного падения на Земле принять равным 9,8 м/с^2.
Результат запиши в системе единиц СИ, округлив до десятых долей.
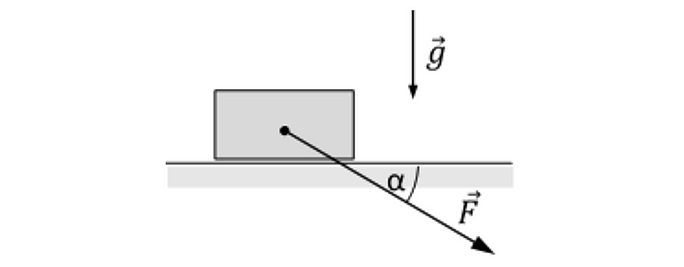
8. Брусок массой m =4 кг, покоящийся на горизонтальной поверхности, пытаются сдвинуть с места, действуя на него силой F =14 Н, направленной под углом =45° к горизонту, как показано на рисунке. При каком минимальном значении коэффициента трения μ бруска о поверхность брусок не будет двигаться?
9. Чтобы тянуть сани в гору с постоянной скоростью, надо прикладывать силу F 1=200 Н под углом φ =30° к поверхности дороги или силу F 2=190 Н вдоль дороги. Определи по этим данным коэффициент трения скольжения μ между санями и дорогой.
Результат округли до сотых долей.
10. Десантник массой m 1=90 кг спускается при открытом парашюте с установившейся скоростью v 1=5 м/с. Какой будет установившаяся скорость, если на том же парашюте спускается мальчик массой m 2=40 кг?
Силу сопротивления воздуха считать пропорциональной квадрату скорости. Результат вырази в м/с, округлив значение до десятых долей.
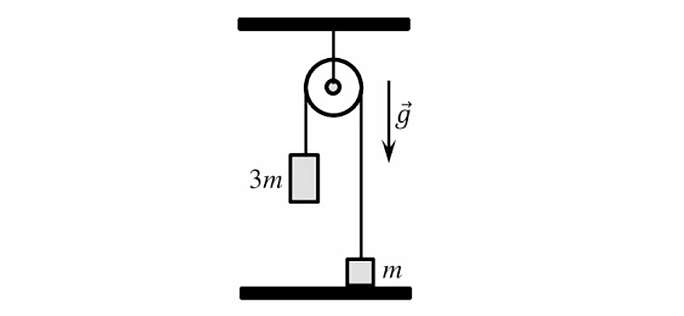
11. Два груза связаны невесомой нерастяжимой нитью, перекинутой через лёгкий блок, прикреплённый к потолку. В начальный момент груз массой m удерживают на поверхности пола, а груз массой 3 m находится на некоторой высоте от этой поверхности. Груз массой m отпускают и через время t =0,6с груз массой 3 m ударяется о пол. Какую скорость имеет этот груз непосредственно перед ударом?
12. В системе, показанной на рисунке, блоки лёгкие, нить невесомая и нерастяжимая, трение отсутствует. Найди ускорение, с которым будет двигаться подвижный блок.
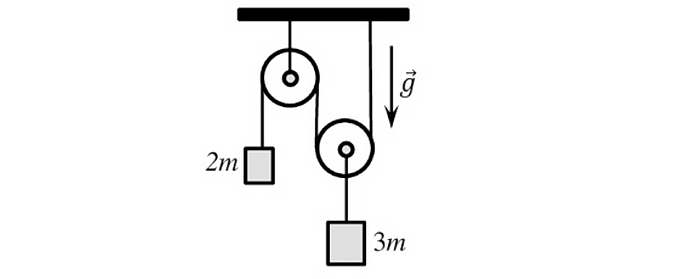
Ускорение свободного падения g =10 м/с^2. Ответ запиши в м/с^2 и округли до десятых долей.
13. Брусок движется по горизонтальной поверхности стола под действием некоторой постоянной горизонтально направленной силы F с ускорением a 1=3 м/с^2. Другой брусок вдвое большей массы, сделанный из такого же материала, под действием той же силы, на том же столе имеет ускорение a 2=1 м/с^2. Найди коэффициент трения μ брусков о поверхность стола.
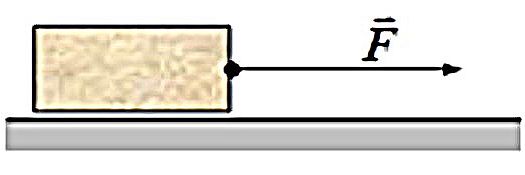
Ускорение свободного падения g =10 м/с^2. Ответ округли до десятых долей.
14. Шайба соскальзывает без начальной скорости с горки, имеющей постоянный угол наклона tgβ (tg β =3/1), за некоторое время. Найди коэффициент трения шайбы о поверхность горки, если известно, что в отсутствие трения время соскальзывания шайбы было бы в два раза меньшим.
Ответ округли до сотых долей.
15. В системе, показанной на рисунке, тела сделаны из одинакового материала и движутся с ускорением а 1=4 м/с^2. Если тела поменять местами, то ускорение их движения станет a 2=5 м/с^2. Найди коэффициент трения тел о горизонтальную поверхность стола.
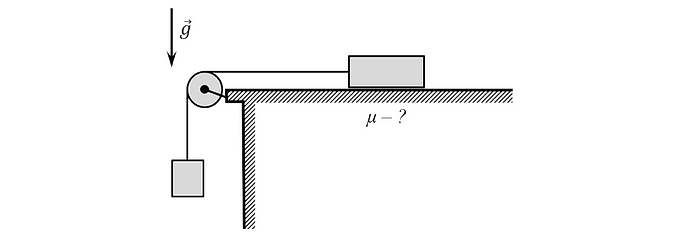
16. В системе, показанной на рисунке, тела движутся с ускорением а 1=6 м/с^2. Если тела поменять местами, то ускорение их движения станет a 2=9 м/с^2. Найди угол наклона поверхности α.
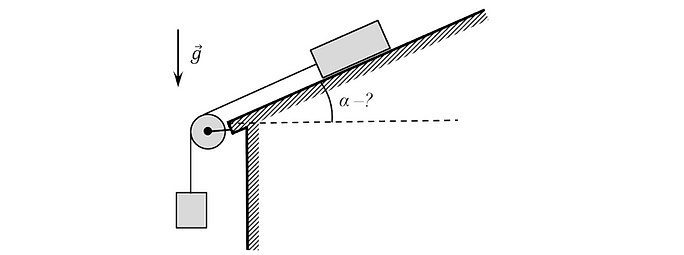
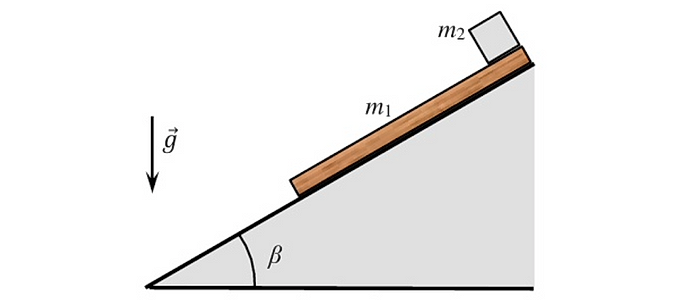
17. На горке с углом наклона β =30° находится доска массой m 1=3 кг и длиной L =2,25 м, на краю которой лежит кубик массой m 2=1 кг (смотри рисунок). В начальный момент доска и кубик покоятся. Найди время соскальзывания кубика с доски, если коэффициент трения доски о поверхность горки μ =0,5, а трением кубика о доску можно
пренебречь.
18. Отважный мальчик съезжает с горы на санках вниз по склону с углом наклона α =45°. Какую максимальную скорость vmax мог он развить, если его масса с санками m =63 кг? Коэффициент трения полозьев санок о снег μ =0,1. Сила сопротивления воздуха пропорциональна квадрату скорости: F = kv 2, где k =0,9 кг/м.
Результат вырази в км/ч и округли до целого.
19. С какими скоростями v1 и v2 будут всплывать в вязкой жидкости два шарика (лёгкий и тяжёлый) одинакового радиуса, связанные длинной тонкой невесомой нерастяжимой нитью при установившемся движении? Известно, что один лёгкий шарик всплывает в этой жидкости со скоростью v0=20 см/с, а тяжёлый имеет нулевую плавучесть (находится в безразличном равновесии в этой жидкости, погружаясь в неё полностью).
Считай, что сила сопротивления жидкости при движении шарика пропорциональна его скорости. Результаты вырази в см/с и округли до целых значений.
20. Небольшой плот массой m =200 кг оттолкнули от берега озера, сообщив ему начальную скорость v0=0,5 м/с. На каком расстоянии L от берега остановится плот? Сила сопротивления движению плота пропорциональна его скорости: F = kv, где k =12,5 Н ⋅ с/м.
Результат вырази в метрах и округли до целого.