Панель, состоящая из ортотропной обшивки и продольных стрингеров и нагруженная системой самоуравновешенных сил

Считаем, что обшивка работает в условиях плоского напряженного состояния, а стрингеры сопротивляются растяжению-сжатию (рис 2.6,а). Тогда в каждой из обшивок возникают усилия , , , а в поясах силы , , .

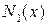Рис. 2.6. Геометрия, нагрузка и усилия в панели: а – рассматриваемая панель;

б – равновесие отсеченной части; в – равновесие элемента стрингера и обшивки

Удовлетворяя уравнениям равновесия проекций сил на оси , и уравнению моментов относительно точки A, получаем с учетом симметрии задачи следующие соотношения между усилиями (рис 2.6,б)

, , ,

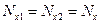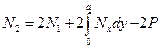, (2.13)

На границе пластины и продольного подкрепления (рис. 2.6,в) выполняется условие равновесия

В обшивке справедливы уравнения равновесия плоской задачи

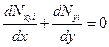, . (2.14)

Интегрируя (2.14), усилия 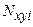и можно выразить через усилия

(2.15)

Для реализации приближенных расчетов представим усилие в виде разложения в ряд по четным производным степени y:

Здесь учитывается симметрия задачи в отношении координаты y. Тогда

Определяем константы интегрирования, удовлетворяя граничные условия по координате y:

при или ;

при и .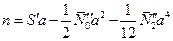

Таким образом, окончательно запишем искомые усилия:

, , ,

, (2.16)

Как видно пять искомых усилий выражаются через три неизвестных функции: , и .

Если в решении задачи пренебречь нормальными напряжениями (), то все известные усилия (при ) выразятся через .

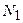Для определения статических неизвестных воспользуемся принципом наименьшей работы. Запишем выражение для дополнительной потенциальной энергии системы, состоящей из обшивки и продольных элементов:

. (2.17)

Подставляя в (2.17) соотношения (2.16) и варьируя по неизвестным 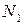, 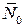и полученный функционал , строим разрешающую систему дифференциальных уравнений совместности деформаций. Эта система достаточно громоздка и приводить здесь не будем.

Упростим решение задачи, считая, что в обшивке изменяется по линейному закону. Если силы в стрингерах и 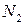, то деформации в них и . Поскольку деформации пластины равны деформациям стрингера по линии контакта, то можно выразить все усилия в пластине через усилия в стрингере.

Закон изменения 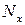в пластине

где и - усилия в пластине по линии контакта со стрингерами I и II

Тогда нормальные усилия для каждой пластины с учетом условий контакта со стрингерами и с учетом (2.13) запишутся в виде

и ,

где .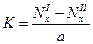

Поскольку деформация стрингера и обшивки по линии контакта равны, то с учетом (2.13) усилия в пластине здесь выражаются через силы 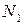и 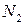в стрингерах

и ,

где .

Согласно (2.13) имеем

. (2.18)

Обозначим через , тогда усилия в обшивке выражаются через силу 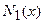стрингера и записываются в следующем виде:

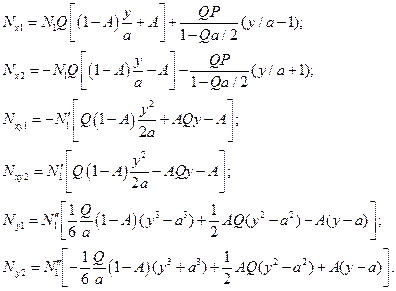(2.19)

Подставляя (2.19) в (2.17) получаем следующий функционал:

Приравнивая вариацию функционала нулю, получим уравнение совместности деформации

, (2.20)

где

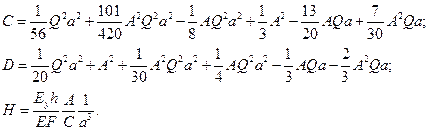
Примем для рассматриваемой панели следующие значения параметров: 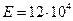МПа; МПа; 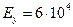МПа; МПа; ; м; м²; м; м.

Для этих параметров коэффициенты дифференциального уравнения:

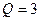м^-1; А = 4; ; ; ; м^-4; ; .

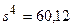Здесь , поэтому решение уравнения (2.20) запишется следующим образом:

где , , .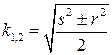

Константы , , 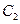, определяются из граничных условий:

при и ;

при и . (2.21)

Отсюда 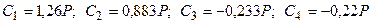, а закон изменения усилий и имеет вид:

; (2.22)

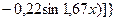Усилия в пластине , и сила в стрингере 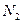определяются в результате подстановки (2.22) в (2.18) и в (2.19).

Если принять что обшивка не воспринимает нормальные напряжения , то во всех соотношениях необходимо положить .

Разрешающее уравнение задачи примет вид:

Обозначая , перепишем уравнение в виде:

, где .

Здесь , тогда корни все действительные, характер решения меняется и принимает вид:

где ; .

Константы определяем из граничных условий (2.21): ; ; ; .

В этом случае функции:

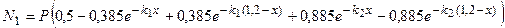; (2.23)

Напряжения в пластине . Если принять, что пластина между стрингерами работает только на сдвиг, т.е. , . В этом случае разрешающее уравнение, полученное на основании принципа наименьшей работы, аналогичное уравнению (2.20) примет вид:

где .

Корни характеристического уравнения , а решение имеет вид:

Для этого решения константы определяются из граничных условий по концам стержня (при , при ): , .

В результате получим решение

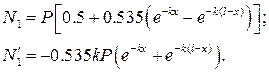(2.24)

Формулы (2.22) - (2.24) представляют решение одной и той же задачи, но с различными допущениями. Первый вариант решения (2.22) является наиболее точным, два других (2,23), (2.24) – менее точными. Указанные варианты решения проиллюстрированы на рисунке 2.7, на котором представлен характер изменения усилий по линии контакта со стрингером, а так же усили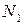й и 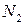по координате x (верхний индекс в

Рис. 2.7. Распределение сил в стрингере и касательных усилий в обшивке

усилиях означает номер варианта). В первых двух вариантах граничные условия удовлетворяются точно. В третьем же варианте, в котором принимается, что пластина вообще не воспринимает нормальных напряжений, граничные условия можно удовлетворить только в стрингере, а на краях панели появляются максимальные касательные напряжения, которых в исходной задаче быть не может.

Изгибаемая панель

Рассмотрим изгибаемую панель, нагруженную поперечными силами в ее плоскости [2]. Все параметры и нагрузка панели, рассматриваемые в этом разделе, приведены на рис. 2.8. Решим эту же задачу в напряжениях и сравним полученные результаты с решением задачи в перемещениях, которая будет рассмотрена дальше.

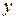
Рис. 2.8. Подкреплённая панель

Рассмотрим первый упрощенный вариант, принимая, что в пластине нормальные усилия меняются по координате 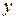по линейному закону и представляются в виде . Предварительно удовлетворим все статические соотношения. Учитывая симметрию поперечного сечения панели, удовлетворим уравнение равновесия моментов в сечении относительно оси . Оно имеет вид

, (2.25)

где - сила в поясе. После интегрирования усилий в пластине выразим составляющую этого усилия через силу 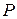на конце панели и силу , т.е. . Тогда усилие запишется в виде

. (2.26)

Удовлетворим уравнения равновесия в стенке

; (2.27)

и с их помощью касательное усилие и нормальное усилие вдоль оси 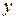выразим через нормальное усилие . Эти усилия принимают вид

; , (2.28)

где и есть функции интегрирования, которые определяются из условий контакта пояса и стенки. При должны выполняться условия и . После подстановки усилия в выражения (2.28), интегрирования по координате 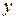и удовлетворения граничных условий выражения (2.28) принимают вид

;

; .

Таким образом, все неизвестные силовые функции напряженного состояния выражаются через усилие в поясе , т.е. задача один раз статически неопределима. Для удовлетворения уравнения совместности деформаций и определения статического неизвестного используем принцип наименьшей работы. Запишем потенциальную энергию конструкции

. (2.29)

После подстановки выражений усилий и интегрирования их по координате 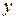потенциальная энергия примет вид

Проварьировав полученный функционал, получим разрешающее уравнение совместности деформаций в виде

, (2.30)

где ; ;

Решение этого уравнения имеет вид

где - комплексные корни характеристического уравнения, если ; 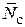- частное решение дифференциального уравнения. Для данной задачи оно имеет вид .

Если корни характеристического уравнения действительные, то решение примет вид

Константы интегрирования определяются из следующих граничных условий:

при 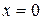; ; , где среднее касательное напряжение в поперечном сечении пояса ; - модуль сдвига сечения; - среднее в сечении значение сдвига, которое равно значению сдвига 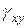в стенке в месте контакта с поясом при . Тогда в этой точке и второе граничное условие принимает вид ;

при ; и .

Если в решении пренебречь влиянием напряжения , то разрешающее дифференциальное уравнение будет второго порядка и вида

где ; .

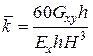Его решение записывается в форме

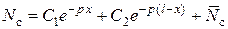где частное решение имеет вид .

В этом случае можно удовлетворить только по одному граничному условию на каждом краю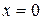: при ; и при ; . Тогда ; и усилия принимают вид, соответствующий усилию для длинной панели, когда один край не влияет на противоположный:

(2.31)

Здесь и - нормальное и касательное усилия в стенке; - сила в продольном подкрепляющем элементе; ; ; - модуль упругости стенки вдоль оси ; - искомая толщина стенки; ; ; 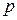- корень характеристического уравнения; - модуль сдвига стенки. В этой задаче в стенке усилие . Для короткой панели константы решения равны:

;

и усилие в поясе принимает вид

Остальные усилия получатся после подстановки в формулы (2.31).

Теперь рассмотрим эту же задачу при условии, что функция усилий 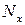меняется по координате 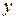пропорционально функции , т.е. . Проделав соответствующие процедуры в соответствии с формулами (2.25) - (2.28) и удовлетворив граничные условия по координате 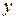для определения и , найдем все необходимые усилия в пластине, выраженные через неизвестное усилие в поясе . Записав энергию в форме (2.29) и проварьировав это выражение по , получим разрешающее уравнение совместности деформаций в прежней форме (2.30), но с новыми значениями коэффициентов ; и . Приведем сравнение решений задач при 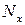в форме (2.25) и виде . Примем следующие расчетные параметры панели: длина панели 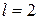м, высота панели 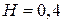м, площади поперечных сечений продольных стержней балок равны см², модуль упругости стержня принят ГПа. Для пластины панели берем композитную однонаправленную ленту со следующими характеристиками: модуль упругости вдоль направления волокон 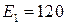ГПа, поперек – 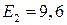ГПа, модуль сдвига ГПа, коэффициент Пуассона , углы укладки 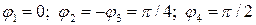и толщины слоев мм, мм. При этих параметрах с помощью программы MAPLE были определены коэффициенты дифференциального уравнения и после его решения и удовлетворения граничных условий были определены все усилия в панели. Коэффициенты характеристического уравнения ; , корни будут действительными числами и равны 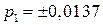и . Расчетные данные приведены на рис. 2.9 и 2.10. На рис. 2.9 приведено распределение усилия вдоль верхнего растянутого стержня, на рис. 2.10 приведено распределение усилия 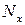в зоне, прилегающей к этому стержню.