Как известно, при подготовке порошкового компакта для эксперимента смесь исходных компонентов предварительно перемешивается и прессуются. При этом в смеси появляется макроскопическая структура концентрационной неоднородности. Поведение таких материалов в условиях ударного нагружения характеризуется различными эффектами: фазовыми переходами, химическими реакциями, межфазным теплообменом и обменом импульсом, термокапилярными эффектами.
Для моделирования этих физико-химических процессов в реагирующей порошковой среде используется компьютерная модель, развитая на кафедре МДТТ.
В модели рассматривается реагирующая шихта, представляющая собой смесь порошков реагирующих компонентов и инертного наполнителя (продукта реакции).
Порошковое тело представляется модельной гетерогенной смесью реагирующих компонентов гафния и бора с инертным наполнителем диборидом гафния, обладающей детерминированными структурными параметрами, физическими и химическими характеристиками. Материал частиц одного сорта считается однородным и изотропным с заданными физическими свойствами. Структура исходной шихты характеризуется формой и размерами частиц и их агрегатов, их расположением, концентрацией компонентов и пористостью. Оценка эффективных физических свойств многокомпонентных материалов ведется с позиции микромеханики композиционных материалов. Поведение всего материала в целом определяется поведением представительного объёма, в качестве которого используется элемент макроскопической структуры концентрационной неоднородности порошкового смеси.
Обычно при интенсивном механическом воздействии происходит увеличение реакционной способности порошковой смеси. За счёт этого происходит понижение порога запуска химических превращений. Степень механической активации определяется интенсивностью механического воздействия. В серии экспериментов по ударному синтезу карбида титана было обнаружено, что существует некоторый интервал амплитуд ударного нагружения в котором, с ростом интенсивности воздействия выход реакции уменьшается. Этот эффект может быть связан с тем, что инициирование химических превращений в процессе действия ударного импульса может привести к локальному изменению агрегатного и фазового состояния материала компонентов порошкового тела, определяя нелинейный характер ударного уплотнения. Для исследования возможных причин такого спада продукта реакции с ростом амплитуда ударного модель была модифицирована с учетом поведения экзотермически реагирующих порошковых материалов типа Ti-C. Тугоплавкий компонент смеси (графит) хрупкий материал и неспособен сопротивляться значительным сдвиговым нагрузкам. Этот фактор позволил построить физическую модель наблюдаемого явления. С некоторого уровня амплитуды динамического воздействия порошковый материал начинает вести себя как суспензия твердых частиц в расплаве. Такое поведение характеризуется уменьшением достижимой степени механической активации. Это определяет специфику физико-химического поведения реагирующей порошковой смеси типа Ti-C [2].
|
|
В порошковой смеси гафний - бор может наблюдаться аналогичное поведение - уменьшение степени механической активации с ростом амплитуды ударного импульса. Это возможно вследствие того, что температуры плавления компонентов смеси (гафний и бор) лежат в одном температурном диапазоне и вследствие этого эта система не способна к формированию тугоплавкого каркаса. Для учёта этого фактора в физической модели порошковой смеси Hf-B допускается возможность плавления поверхностных слоёв частиц гафния и бора одновременно.
|
|
Описание математической модели.
Процессы ударной модификации порошкового тела моделируются с позиции механики пористых упругопластических сред. Между фронтом ударного импульса и областью конечных состояний находится зона перехода, ширина которой определяется временем затухания циркулирующих в частицах волн сжатия и разгрузки и временем тепловой релаксации частиц. Диссипация кинетической энергии колебаний материальных частиц по механизмам пластического деформирования и разрушения поверхностных слоёв частиц реагирующих компонент приводит к активации компонентов смеси и появлению тепловой составляющей в уравнении баланса энергии. К исследованию процессов ударной модификации порошковых компонентов применяется подход микромеханики композиционных материалов. Эффективные параметры среды за фронтом ударного импульса использованы как средние параметры нагружения представительного объёма реагирующего компонента. Законы сохранения массы, импульса и энергии при ударном сжатии и разогреве порошковой смеси рассмотрены без использования формальной величины средней плотности пористой среды:
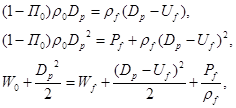(1)
|
|
где Dp - скорость ударного импульса в пористой среде, Uf - массовая скорость, Pf - давление на фронте ударного импульса, W0, Wf - удельные внутренние энергии среды до и после ударного нагружения, ρ0, ρf -плотности материала перед и за фронтом ударного импульса, П0 - начальный относительный объём пор.
В левой части записаны аддитивные характеристики для частиц перед фронтом ударного импульса, а правая часть описывает параметры сплошной среды за фронтом. При динамическом воздействии частицы нагружаются ударным импульсом, а затем разгружаются в окружающие их поры. Эффективные параметры среды за фронтом ударного импульса, полученные по модели Тувинина [7], представляются в виде:
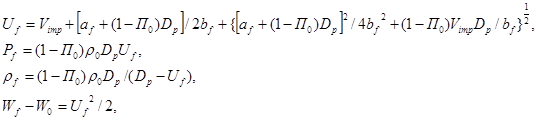(2)
где af, bf - параметры ударной адиабаты, Dp - скорость ударного импульса в пористой среде, Uf - массовая скорость, Рf - давление на фронте ударного импульса, W0, Wf - удельные внутренние энергии среды до и после ударного нагружения, ρ0, ρf - плотности материала перед и за фронтом ударного импульса, Пo- начальный относительный объём пор, Vimp - скорость «эквивалентного» ударника.
Параметры ударных адиабат смесевых порошковых сред выражаются через параметры адиабат для компонентов:
,
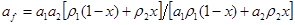, (3)
где х - массовая доля одного из компонентов, ρ - плотность, а, b -ударные адиабаты компонентов, индексы 1 и 2- описывают компоненты смеси.
Тепловые процессы в зернистом слое определяются выражениями
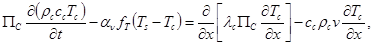
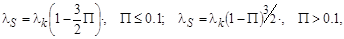
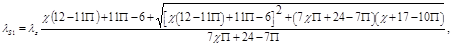
где коэффициент теплопроводности,
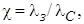коэффициент теплопроводности в насыщенном жидкой фазой зернистом теле.
Вынужденная фильтрация жидкой фазы определяется соотношением (закон Дарси)
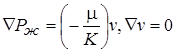
Зависимость вязкости от температуры
Проницаемость пористой среды
Поровое давление определяется следующими соотношениями
Выход продукта реакции считается по следующему выражению
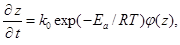
Условие реакционной эквивалентности
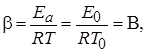
Изменение реакционной способности
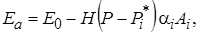
Предэкспоненциальный множитель
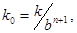
Микромеханика процесса пластического деформирования пористой среды представляется процессом сферически симметричного схлопывания и реализации струйных течений. Пористая среда моделируется единичной ячейкой Нестеренко [8] в виде полой сферы с центральной частицей.
Процесс затекания пор гетерогенной среды под действием ударного импульса оценивается покомпонентно с привлечением модели единичной ячейки Нестеренко. Модельная ячейка позволяет определить термодинамическое состояние системы в локальных микрослоях элемента структуры порошковой среды. В процессе ударного перехода запасенная энергия ударного импульса диссипирует по различным механизмам, смена которых для каждого компонента порошковой смеси моделируется поэтапно. Реальное порошковое тело (справа) представляется модельной ячейкой пористой среды в виде полой сферы с центральным сферическим включением, представленная на рис. 1.
рис. 1. Модельная сферически-симметричная ячейка
Геометрические параметры модели Нестеренко:
, 
,
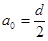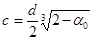, (4)
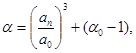
где α, α0 - параметры, характеризующие пористость, d- диаметр частицы.
Учитывается зависимость предела текучести и вязкости пластического течения от температуры:
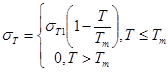(5)
где σT1 - характерное значение предела текучести при низких температурах, Tm - температура плавления;
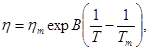(6)
где ηm - вязкость расплава.
Термодинамика ударного сжатия порошкового материала определяет доли кинетической энергии ударного импульса, затраченные на совершение работы по пластическому затеканию пор в статическом и динамическом режимах.
В статическом режиме энергия ударного импульса диссипирует в результате пластического и вязкого течений. В каждый момент действия ударного импульса для известной квоты энергии, диссипированной при пластическом деформировании уравнения (7) решаются относительно пористости П1.
Остальная часть энергии ударного импульса может диссипировать в гидродинамическом режиме. В около поверстных слоях частиц формируются струйные течения, в итоге это приводит к разрушению поверхностных слоёв частиц, т. е. к разрушению окисных и сорбированных плёнок.
Удельная энергия деформирования без учёта процессов вязкой диссипации:
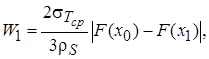
(7)
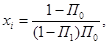
где 
- предел текучести.
Удельная тепловая энергия ударного сжатия представленная в виде (1) считается для каждого реагирующего компонента:
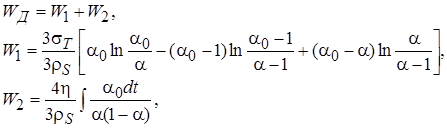(8)
где W1, W2 - средние величины диссипированной энергии при пластическом и вязком течении. Разница между удельной энергией сжатия Wt и удельной энергией WД, диссипируемой в окрестности сферической поры на стадии её схлопывания, представляет собой микрокинетическую энергию:
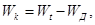
она расходуется на очищение поверхностных контактных слоев частиц, и, уплотнение порошкового материала за счёт того, что в поверхностных слоях частиц возникает жидкоподобное поведение материала [8]. С увеличением импульса приложенной нагрузки уменьшается доля энергии, диссипированной на пластическую деформацию и вязкое затекание пор, а значит, растёт доля энергии, которая затрачивается на разрушение поверхностных слоев частиц.
Если в поверхностных слоях реагирующих частиц возникает расплавление материала, то порошковый материал будет вести себя как пористая суспензия взаимодействующих твёрдых частиц (гафния и бора) в расплаве. При этом вязкость суспензии будет существенно меньше эффективной вязкости исходной порошковой среды. Уплотнение порошкового материала под действием ударного импульса будет происходить в режиме вязкого уплотнения пористой суспензии без пластического деформирования всего объёма материала.
Скорость прогрева частиц в процессе пластического деформирования компонентов порошкового тела определяется соотношениями, полученными для модельной единичной ячейки. Эти соотношения представляют параболическую зависимость скорости изменения температуры от величины [2].
,
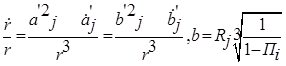Прирост температуры в поверхностном слое частиц определяется соотношением (9) и считается для каждого из компонент отдельно:
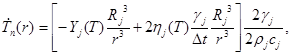(9)
где 
- предел текучести,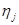 
- динамическая вязкость, 
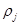- плотность,
-теплоёмкость,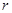 
- расстояние от центра модельной ячейки, 
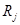радиус частицы, индекс 
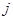относится к номеру компонента смеси.
Общий прогрев поверхностного слоя модельной ячейки после запуска механохимических превращений на шаге по времени определяется источниками тепла механической и химической природы, а также тепло потерями на фазовые переходы:
(10)
где Z - степень превращения тугоплавкого компонента, Q - тепловой эффект реакции,
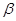- тепловые потери, 
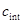- теплоёмкость продукта реакции.
Для каждой частицы решаются модельная задача о прогреве частицы. Решением этой задачи может быть представлено в виде 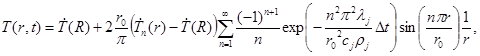(11):
(11)
Из уравнения (11) оценивается относительный объём расплавленного слоя частиц реагирующих компонентов
Температуры плавления компонентов смеси (гафния и бора) лежат в одном температурном диапазоне (примерно 24000 К). С момента появления жидкого слоя на поверхности частиц материал начинает вести себя как суспензия. Вязкость суспензии может быть оценена с привлечением модели Шишкина [2]. Эта модель используется, потому что она адекватна для небольших количеств жидкости в суспензии, в модели смена режима уплотнения происходит как раз при количестве жидкости около 1%. Вязкость суспензии можно определить соотношениями:
,
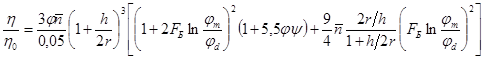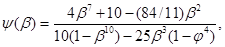
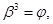
где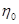 
- вязкость расплава, 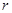- радиус частицы, 
- расстояние между частицами;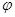 
- текущая объёмная концентрация, 
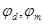- максимальные концентрации, отвечающие нулевой и предельной дилатансии (теплового расширения) для данного материала, 
- координатное число.
В процессе спекания вязкость суспензии может понизиться до определённого уровня, с которого затекание пор будет происходить по другому механизму: с вязкопластического течения деформируемых твердых порошковых частиц на вязкопластическое течение суспензии взаимодействующих частиц в расплаве, что приводит к уменьшению интенсивности химических превращений.