ВЫЧИСЛИТЕЛЬНЫЙ ЭКСПЕРИМЕНТ

Для моделирования физико-химических процессов в реагирующей порошковой среде используется компьютерная модель, развитая на кафедре МДТТ. Рассмотрена следующая модель смены механизма внутреннего трения в порошковом компакте смеси гафния и бора в процессе динамического уплотнения. При действии ударного импульса первоначально деформируются наружные слои порошковых частиц. Это вызывает термическую и механическую активацию поверхностных контактирующих слоёв частиц реагирующих компонентов. Если в результате этого запускается экзотермические химические превращения в локальных зонах контакта частиц, то на поверхности частиц реагирующего компонента может появиться жидкий слой «легкоплавкого» компонента, который не оказывает сопротивления локальным сдвиговым нагрузкам. В этом случае порошковый материал будет вести себя как пористая суспензия взаимодействующих твёрдых частиц в расплаве, вязкость которой существенно меньше эффективной вязкости исходной порошковой среды. Под действием ударного импульса происходит уплотнение порошкового компакта в режиме вязкого уплотнения пористой суспензии взаимодействующих твёрдых частиц в расплаве без пластического деформирования всего объёма материала частиц [2].

В качестве основных допущений при моделировании процессов ударного синтеза принято считать, что:

) ударное нагружение порошкового компакта может быть представлено макроскопическим плоским импульсом, распространяющимся в главном направлении с заданными с заданными амплитудой P_f и длительностью;

) моделирование физико-химических процессов ударного синтеза включает в себя моделирование процессов теплопереноса в реагирующем слое, процессов ударной модификации порошкового тела, фазовых переходов компонентов порошковой смеси, массопереноса и химических превращений;

) образовавшаяся жидкая фаза «легкоплавкой» компоненты может перемещаться в пористом каркасе, обеспечивая конвективный тепло- и массоперенос. В этом случае закон сохранения энергии представляется двухтемпературными уравнениями теплопереноса с переменами коэффициентами, источниками и стоками;

) прогрев и экзотермическая реакция синтеза рассматриваются в области температур, ограниченной температурными фронтами [T₀, T₁). Здесь Т₀ - начальная температура смеси, а Т₁ - температура реагирующей смеси, при которой пористый каркас теряет несущую способность. Процессы «дожигания» смеси при температурах, больших Т₁, не исследуются [9].

Для того чтобы проверить гипотезу, сформулированную в цели работы, модель была модифицирована, так что появилась возможность учета плавления поверхностных слоёв частиц гафния и бора одновременно. В первоначальной модели для смеси титан - графит температуры плавления компонентов отличались в два раза и поэтому только один из компонентов (титан) мог расплавиться. Для учета плавления поверхностных слоёв частиц гафния и бора одновременно были внесены следующие изменения в модели.

Прирост температуры в поверхностном слое частиц, вызванный вязкопластическим деформированием, определяется соотношением (2), после изменения модели рассматривается для каждого из компонентов смеси отдельно:

(2)

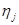где - предел текучести, - динамическая вязкость, 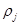- плотность,

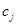-теплоёмкость, 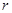- расстояние от центра модельной ячейки, 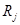радиус частицы, индекс относится к номеру компонента смеси.

Как следствие общий прогрев поверхностного слоя модельной ячейки после запуска механохимических превращений так же считается для каждого компонента отдельно и определяется источниками тепла механической и химической природы, а также тепло потерями на фазовые переходы:

(3)

где Z - степень превращения тугоплавкого компонента, Q - тепловой эффект реакции, 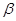- тепловые потери на фазовые переходы, - теплоёмкость продукта реакции.

Для каждой частицы решаются модельная задача о прогреве частицы, а изначально модельная задача решалась только для одной частицы. Решением этой задачи может быть представлено в виде (4):

(4)

из которого оценивается относительный объём расплавленного слоя частиц реагирующих компонентов.

С момента появления жидкого слоя на поверхности частиц материал начинает вести себя как суспензия. Зная суммарный объём жидкого слоя частиц можно рассчитать вязкость суспензии при помощи модели Шишкина, эта модель используется, потому что она адекватна для небольших количеств жидкости в суспензии, в модели, смена режима уплотнения происходит как раз при количестве жидкости около 1%:

,

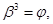
где - вязкость расплава, - радиус частицы, - расстояние между частицами; - текущая объёмная концентрация, - максимальные концентрации, отвечающие нулевой и предельной дилатансии (расширение) для данного материала, - координатное число, коэффициент теплопроводности.