Для группы ЭЭ-11-11-варианты с 1-го по 30, ЭЭ-12-11-с 31-го.
1 Задана окружность 
и две точки P =(P 1, P 2) и F =(F 1, F 2). Выяснить и напечатать, сколько точек лежит внутри окружности. Проверку, лежит ли точка внутри окружности, оформить в виде процедуры-функции.
2 Три точки заданы своими декартовыми координатами Х =(Х 1, Х 2), Y =(Y 1, Y 2), Z =(Z 1, Z 2). Вычислить и выдать на печать полярные координаты этих точек. При выдаче на печать координаты точек упорядочить по возрастанию полярного радиуса R. Полярный радиус R и полярный угол 
вычисляется по следующим формулам: 
, 
. Перевод в полярные координаты оформить в виде подпрограммы.
3 Даны пять различных целых чисел. Найти среди них два числа, модуль разности которых имеет наибольшее значение.
4 Построить таблицу функции z =sh(x + y),где x меняется от 1 до 2 с шагом 0,2, а y меняется от 2 до 3 с шагом 0,1. Гиперболический синус вычисляется по формуле 
. Вычисления гиперболического синуса оформить в виде процедуры.
5 Заданы две матрицы А и В. Построить таблицу функции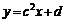 
при х, меняющемся от 0 до 1 с шагом 0,1, где с - след матрицы А; d - cлед матрицы В (след матрицы - сумма элементов главной диагонали). Вычисление следа матрицы оформить в виде подпрограммы.
6 Даны целые числа m, a 1, a 2,..., a 20. Найти два натуральных числа a i и a j, каждое из которых не превосходит 20, такие, что ai + aj = m. Если таких чисел нет, то сообщить об этом.
7 Четыре точки заданы своими координатами X =(X 1, X 2, X 3), Y =(Y 1, Y 2, Y 3), Z =(Z 1, Z 2, Z 3), P =(P 1, P 2, P 3). Выяснить, какие из них находятся на минимальном расстоянии друг от друга. Вычисление расстояния между двумя точками оформить в виде подпрограммы-функции.
8 Заданы два массива A ={ A 1,..., A 4}, B ={ B 1, B 2,..., B 6}. Переменной S присвоить значение -1, если максимальный элемент массива A больше максимального элемента массива B; 0, если они равны, и 1, если максимальный элемент массива A меньше максимального элемента массива B. Поиск максимального массива оформить в виде подпрограммы.
|
|
9 Вычислить значение компонент вектора Х по формуле 
, i =1,...,20. Полученный вектор вывести на экран. Переменной Z присвоить значение 1, если компоненты вектора Х образуют монотонно возрастающую последовательность (x 1< x 2...< x 20), и значение 0 - в противном случае.
10 Образовать вектор а из членов последовательности cos(x), cos(x + h),..., cos(x +20 h). Вектор а вывести на печать. Найти сумму тех членов последовательности, которые по модулю больше 0,5.
11 Вычислить значения компонент вектора x ={ x 1,..., x 15} по формуле 
. Записать в файл полученный вектор. Найти сумму компонент вектора x, принадлежащих отрезку [-0,5; 0,5] и число таких компонент.
12 Дано натуральное число n. Среди чисел 1,..., n найти все такие, которые делятся без остатка на 3, 5, 7, 9. Нахождение кратных чисел оформить в виде процедуры.
13 Дан вектор Х ={ Х 1, Х 2,..., Хк }. Осуществить циклический сдвиг компонент этого вектора влево на одну позицию, т.е. получить вектор Х ={ Х 2, Х 3,..., Хк, Х 1}.
14 Заданы два вектора х и у. Переменной Z присвоить значение 1, если длина вектора х больше длины у, и присвоить значение 0 в противном случае. Вычисление длины вектора оформить в виде процедуры (длина вектора вычисляется по формуле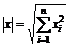 
).
15 Заданы два вектора X ={ x 1, x 2, x 3, x 4}, Y ={ y 1, y 2, y 3, y 4}. Определить 
, где (X, Y) - скалярное произведение векторов;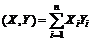 
. Вычисление оформить в виде процедуры.
16 Четыре точки X, Y, Z, P заданы своими координатами. Выяснить, какие из них находятся на максимальном расстоянии друг от друга, и вывести на печать значение этого расстояния. Вычисление расстояния между двумя точками оформить в виде подпрограммы.
|
|
17 Даны целые числа a ={ a 1, a 2,…, an }. Для каждого из чисел, входящих в последовательность { a }, выяснить, сколько раз оно входит в эту последовательность.
18 Дан вектор Y ={ у 1, у 2, у 3,..., у 2 n } (n ³15). Получить из него вектор Z ={ у 1+ y 2 n, y 2+ y 2 n -1,..., yn + yn +1}. Вывести на печать векторы Y и Z.
19 Дана вещественная квадратная матрица порядка n. Построить вектор Z ={ z 1, z 2,.., zn }. zi =2 если все элементы строки i четные, zi =1 - в противном случае.
20 Даны три вектора { k },{ l },{ m }. Найти большее из скалярных произведений (k, l), (k, m), (l, m). (Скалярное произведение векторов вычисляется по формуле 
.) Вычисление скалярного произведения оформить в виде подпрограммы.
21 Заданы три матрицы А (2´2), В (3´3), С (3´3). Решить уравнение 
, где а, b, с - средние арифметические значения элементов матриц А, В, С соответственно. Вычисление среднего арифметического оформить в виде процедуры-функции.
22 Даны действительные числа а 1,.., аn, b 1,..., bn. Вычислить (a 1+ bn)(a 2+ bn -1)...(an + b 1). Подсчитать количество положительных чисел в последовательностях { a } и { b }. Подсчет положительных чисел оформить в виде процедуры.
23 Дана вещественная матрица А (4´4). Заменить нулями в матрице элементы с четной суммой индексов.
24 Даны четыре точки А (х 1, у 1), В (х 2, у 2), С (х 3, у 3), D (х 4, у 4) и переменная Z. Присвоить Z значение 1, если площадь круга с радиусом АВ больше площади круга с радиусом CD, и 0 - в противном случае. Все геометрические вычисления, т.е. нахождение радиусов и площадей кругов, оформить отдельными процедурами.
|
|
25 Даны векторы А ={ а 1,..., а 15}, В ={ b 1,..., b 15}. Переменной Z присвоить значение 1, если вектор А содержит больше чисел, делящихся без остатка на 3, чем вектор В, и значение 0 - в противном случае. Подсчет чисел оформить отдельной процедурой.
26 Даны действительные числа s, t. Получить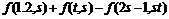 
, где 
. Нахождение 
оформить в виде подпрограммы.
27 Дана вещественная матрица А (5´5) и число m. Заменить все элементы i -й строки матрицы на 1, если сумма элементов в этой строке меньше m, в противном случае оставить i -ю строку без изменения. Нахождение суммы элементов строки оформить в виде подпрограммы.
28 Даны действительные числа Х, Y 1,..., Y 100 (Y 1< Y 2<...< Y 100, Y 1< X < Y 100). Найти натуральное k, при котором Yk -1< X < Yk,
29 Дано число n <= 15. Выяснить, имеются ли среди чисел n +1,...,2 n простые числа, разность между которыми равна двум. Вывести на экран пары простых чисел. Нахождение простых чисел оформить в виде подпрограммы.
30 Дан вектор А ={ а 1, a 2,..., a 2 n }. Получить из него вектор A ={ a 1, an +1, a 2, an +2,..., an, a 2 n }. Вывести на печать исходный и преобразованный вектор.
31 Дана матрица А (5´5). Получить вектор В ={ b 1, b 2, b 3, b 4, b 5} такой, что bi равно среднему арифметическому i -й строки матрицы А. Нахождение среднего арифметического оформить в виде процедуры.
32 Получить таблицу температур по Цельсию от 0 до 100 градусов и их эквивалентов по шкале Фаренгейта, используя для перевода формулу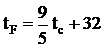 
. Вывести результаты на экран и в файл.
33 Даны действительные числа x 1, y 1, x 2, y 2,..., x 10, y 10. Найти периметр десятиугольника, вершины которого имеют соответственно координаты (x 1, y 1), (x 2, y 2),..., (x 10, y 10). Нахождение длин сторон прямоугольника оформить в виде подпрограммы.
34 Даны действительные числа а, b, с. Получить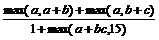 
. Нахождение наибольшего из двух чисел оформить в виде отдельной функции.
35 Дана квадратная матрица порядка n. Получить вектор Ab, где b – вектор, элементы которого вычисляются по формуле 
36 Дано двадцать целых чисел. Выяснить, сколько чисел входит в эту последовательность по одному разу.
37 Даны три точки А (х 1, у 1), В (х 2, у 2), С (х 3, у 3) - вершины треугольника. Выяснить, является ли данный треугольник равнобедренным. Нахождение длин сторон оформить в виде подпрограммы.
38 Задана вещественная матрица А. Построить векторы В и С по правилу: bi - наибольшее значение i -й строки, ci - квадрат наименьшего числа строки
39 Заданы два вектора X ={ x 1, x 2, x 3, x 4}, Y ={ y 1, y 2, y 3, y 4}. Вычислить 
, где (X, Y) - скалярное произведение векторов; 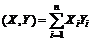. Вычисление оформить в виде отдельной подпрограммы-функции.
40 Даны пять кругов с радиусами r 1, r 2, r 3, r 4, r 5 и А (х 1, у 1), В (х 2, у 2), С (х 3, у 3), D (х 4, у 4), Е (x 5, y 5) - точки центров. Указать:а) два круга с одинаковой площадью (если есть); б) круги имеющие наибольшую и наименьшую площади. Вычисление площади круга оформить в виде процедуры.
41 Дана вещественная квадратная матрица порядка 15. Выяснить, имеются ли в матрице элементы, кратные четырем. Если такие элементы имеются, то указать их индексы
42 Дано действительное число х. Вычислить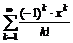 
с точностью e.
43 Дана действительная матрица размера n ´ m. Получить последовательность b 1,…, bn, где bk – число отрицательных элементов в k -м столбце. Вычисление элементов последовательности b 1,…, bn оформить в виде процедуры.
44 Заданы значения трех случайных величин: a ={ a 1, a 2, a 3}, b ={ b 1, b 2, b 3, b 4}, c ={ c 1, c 2, c 3, c 4, c 5}. Найти максимальное из трех чисел x, y, z, где х=М[a], y=M[b], z=M[c]. (
- математическое ожидание случайной величины q ={ q 1, q 2,..., qn }). Вычисление математического ожидания оформить в виде подпрограммы-функции.
45 Даны действительные числа x,e. Вычислить сумму ряда с точностью e и указать количество учтенных слагаемых: 
.
46 Дана вещественная квадратная матрица порядка n. В строках с отрицательными элементами на главной диагонали найти наибольший и наименьший элементы. Элементы матрицы считать из файла. Чтение элементов из файла, а также контрольный вывод матрицы оформить в виде отдельных подпрограмм.
47 Даны действительные числа x, y - координаты центра окружности, радиус r и две точки p ={ p 1, p 2}, f ={ f 1, f 2}. Выяснить и напечатать, сколько точек лежит внутри окружности. Проверку, лежит ли точка внутри окружности, оформить в виде отдельной функции.
48 Решить уравнение dx = c, где d - длина вектора a ={ a 1, a 2, a 3, a 4}; с - длина вектора b ={ b 1, b 2, b 3} (длина вектора вычисляется по формуле 
). Вычисление длины вектора оформить в виде подпрограммы-функции.
49 Дана действительная квадратная матрица порядка n. Построить последовательность а 1,..., аn по правилу: если в i -й строке матрицы элемент, принадлежащий главной диагонали, отрицателен, то ai равно сумме элементов i -й строки; в противном случае ai=0. Вычисление элементов последовательности а 1,..., аn оформить в виде процедуры.
50 Даны действительные числа x,e. Вычислить с точностью e бесконечную сумму и указать количество учтенных слагаемых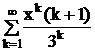 
.
51 Дана вещественная матрица размером n ´ m. Найти b 1,…, bm, где bi – сумма максимального и минимального элементов i -го столбца. Элементы матрицы считать из файла. Вычисление элементов последовательности b 1,…, bm оформить в виде процедуры.
52 Дана вещественная матрица размером n ´ m. Найти b 1,…, bm, где bi – сумма квадратов элементов i -го столбца, модули которых принадлежат отрезку [1,10]. Элементы матрицы считать из файла. Вычисление элементов последовательности b 1,…, bm оформить в виде процедуры.
53 Даны векторы А ={ а 1,..., а 15}, В ={ b 1,..., b 15}. Переменной Z присвоить значение 1, если вектор А содержит больше отрицательных четных чисел, чем вектор В, и значение 0 - в противном случае. Подсчет чисел оформить отдельной процедурой.
54 Вычислить значения компонент вектора x ={ x 1,…, x 15} по формуле xi =(cos0,3 i +sin7 i)/tg(5 i). Записать в файл полученный вектор. Найти сумму компонент вектора х, принадлежащих отрезку [-0,65;0,65], и число таких компонент.
55 Даны точки А (х 1, у 1), В (х 2, у 2), С (х 3, у 3), D (х 4, у 4) - координаты кругов с радиусами r 1, r 2, r 3, r 4. Получить вектор Z ={ z 1, z 2, z 3, z 4}. zi =1, если i -я окружность лежит выше оси абсцисс, в противном случае - zi =0. Определение, лежит ли окружность в заданной области, оформить в виде процедуры.
56 Заданы четыре вектора { x },{ y },{ z },{ p }. Переменной А присвоить значение 1, если скалярное произведение векторов (х, у) больше скалярного произведения векторов (z, p), и значение 0- в противном случае. Вычисление скалярного произведения оформить в виде процедуры. Скалярное произведение вычисляется по формуле 
.
57 Заданы матрицы А (2´2), В (3´3). Решить уравнение px + d =0, где р – сумма минимального и максимального элементов матрицы А; d - сумма минимального и максимального элементов матрицы В. Поиск минимального, максимального элементов матрицы, а также их суммирование оформить в виде процедуры.
58 Заданы вещественные векторы a ={ a 1, a 2,..., an } и x ={ x 1, x 2,..., xn }. Преобразовать вектор х по правилу: если аi>0, то xi возвести в куб и поделить на 10, в противном случае изменить знак xi на противоположный.
59 Дано двадцать целых чисел. Выяснить, сколько чисел входит в эту последовательность больше одного раза.
60 Дана вещественная матрица порядка (5´5). Найти b 1, b 2, b 3, b 4, b 5, где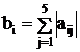 
. Элементы матрицы считать из файла. Вычисление элементов последовательности b 1, b 2, b 3, b 4, b 5 оформить в виде подпрограммы.
61 Дано действительное число e (e>0). Последовательность a 1, a 2,…, an образована по закону 
. Найти первый элемент аn (n ³2), для которого выполняется условие 
.
62 Заданы две матрицы А и В. Построить таблицу функции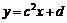 
при х, меняющемся от 0 до 1 с шагом 0,1, где с – сумма элементов матрицы А, лежащих выше и на главной диагонали; d - сумма элементов матрицы В, лежащих выше и на главной диагонали. Вычисление суммы элементов матрицы, лежащих выше и на главной диагонали, оформить в виде подпрограммы.