Случайное отклонение должно быть независимо от объясняющих переменных.

Вопрос

КОРРЕЛЯЦИЯ ДЛЯ НЕЛИНЕЙНОЙ РЕГРЕССИИ

Уравнение нелинейной регрессии, так же как и в линейной зависимости, дополняется показателем корреляции, а именно индексом корреляции:

Так как , а 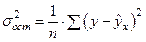, то индекс корреляции можно выразить так:

Величина данного показателя находится в пределах , чем ближе к единице, тем теснее связь рассматриваемых признаков, тем более надежно найденное уравнение регрессии.

Если нелинейное относительно объясняемой переменной уравнение регрессии при линеаризации принимает форму линейного уравнения парной регрессии, то для оценки тесноты связи может быть использован линейный коэффициент корреляции, величина которого в этом случае совпадет с индексом корреляции.

Поскольку в расчете индекса корреляции используется соотношение факторной и общей суммы квадратов отклонений, то 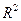имеет тот же смысл, что и коэффициент детерминации. В специальных исследованиях величину 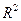для нелинейных связей называют индексом детерминации.

Индекс детерминации используется для проверки существенности в целом уравнения нелинейной регрессии по -критерию Фишера:

где 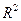– индекс детерминации;

– число наблюдений;

– число параметров при переменных .

Величина характеризует число степеней свободы для факторной суммы квадратов, а – число степеней свободы для остаточной суммы квадратов.

Расчет F- критерия можно вести и в таблице дисперсионного анализа результатов регрессии, как это было показано для линейной функции.

Индекс детерминации можно сравнивать с коэффициентом детерминации для обоснования возможности применения линейной функции. Чем больше кривизна линии регрессии, тем величина коэффициента детерминации меньше индекса детерминации . Близость этих показателей означает, что нет необходимости усложнять форму уравнения регрессии и можно использовать линейную функцию. Практически если величина 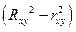не превышает 0,1, то предположение о линейной форме связи считается оправданным.

В противном случае проводится оценка существенности различия , вычисленных по одним и тем же исходным данным, через -критерий Стьюдента:

где – ошибка разности между 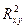, определяемая по формуле

Если , то различия между рассматриваемыми показателями корреляции существенны и замена нелинейной регрессии уравнением линейной функции невозможна. Практически если величина , то различия между 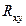и несущественны, и, следовательно, возможно применение линейной регрессии, даже если есть предположения о некоторой нелинейности рассматриваемых соотношений признаков фактора и результата.

Вопрос

Предпосылки МНК

1. Математическое ожидание случайного отклонения εi равно нулю: M(εi)=0 для всех наблюдений.

Данное условие означает, что случайное отклонение в среднем не оказывает влияния на зависимую переменную. Выполнимость M (ε i) =0 влечет выполнимость:

M (Y X=xi)= β0 +β1xi.

2. Дисперсия случайных отклонений εi постоянна: D(εi)=D(εj)=σ2ε =const для любых наблюдений i и j.

Условие независимости дисперсии ошибки от номера наблюде-

ния называется гомоскедастичностью Невыполнимость

данной предпосылки называется гетероскедастичностью.