Тема 1. Предел функции
Число А называется пределом функции  при
при  , стремящимся к
, стремящимся к 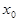 , если для любого положительного числа
, если для любого положительного числа 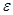 (
(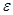 >0) найдется такое положительное число
>0) найдется такое положительное число  >0 (зависящее в общем случае от
>0 (зависящее в общем случае от 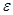 ), что для всех
), что для всех  , не равных
, не равных 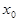 и удовлетворяющих условию x
и удовлетворяющих условию x  x<
x<  , выполняется неравенство x
, выполняется неравенство x  А x<
А x< 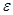 .
.
Для предела функции вводится обозначение 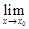
 =А.
=А.
Пределы функций обладают следующими основными свойствами:
Функция не может иметь более одного предела.
Если  = С (постоянная), то
= С (постоянная), то 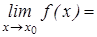 С.
С.
Если существует  А, то для любого числа
А, то для любого числа  верно:
верно:
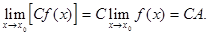
Если существуют  А и
А и  В, то
В, то  =
=  АВ,
АВ,  а если В
а если В  0, то
0, то
 .
.
Операция предельного перехода перестановочна с операцией вычисления непрерывной функции, т. е. справедлива формула 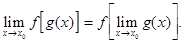
Если функция  непрерывна в точке
непрерывна в точке 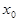 , то искомый предел равен значению функции в этой точке, т.е. он находится непосредственной подстановкой предельного значения переменной вместо аргумента
, то искомый предел равен значению функции в этой точке, т.е. он находится непосредственной подстановкой предельного значения переменной вместо аргумента  :
: 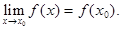
Функция  (
( называется бесконечно малой величиной при
называется бесконечно малой величиной при 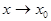 , если ее предел равен нулю:
, если ее предел равен нулю:  Функция
Функция  называется бесконечно большой величиной при
называется бесконечно большой величиной при 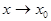 , если
, если 
Пример 1. 

 9.
9.
Пример 2. 
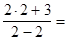

 .
.
В рассмотренных примерах предел находился сразу: в виде числа или символа  (бесконечность). Но чаще при вычислении пределов мы встречаемся с неопределенностями, когда результат нахождения предела не ясен, например, в случае отношения двух бесконечно малых функций (условное обозначение
(бесконечность). Но чаще при вычислении пределов мы встречаемся с неопределенностями, когда результат нахождения предела не ясен, например, в случае отношения двух бесконечно малых функций (условное обозначение  ) или бесконечно больших (
) или бесконечно больших ( ).Кроме названных встречаются неопределенности вида
).Кроме названных встречаются неопределенности вида 
Для раскрытия неопределенностей используются специальные приемы и два следующих предела, которые играют особую роль в математике и поэтому называются замечательными:
- первый замечательный предел 
-второй замечательный предел  (число Эйлера).
(число Эйлера).
Пример 3.  .
.
Решение. Непосредственной подстановкой убеждаемся, что имеем дело с неопределенностью вида  :
:
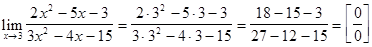 .
.
Для раскрытия неопределенности разложим числитель и знаменатель на множители. Найдем корни многочлена, стоящего в числителе. Для этого составим уравнение второй степени  и найдем его решение:
и найдем его решение:


Тогда для квадратного трехчлена справедливо разложение на множители
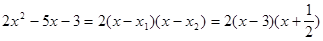 .
.
Аналогичные действия выполним для многочлена, стоящего в знаменателе.
Уравнение  имеет решения
имеет решения


и знаменатель представляется в виде: 
Сократим дробь на множитель 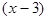 и вычислим ее при
и вычислим ее при 

Пример 4. 
Решение. Непосредственной подстановкой убеждаемся, что возникает неопределенность вида  . Для раскрытия неопределенности умножим числитель и знаменатель на выражение
. Для раскрытия неопределенности умножим числитель и знаменатель на выражение  , являющееся сопряженным к знаменателю
, являющееся сопряженным к знаменателю

=  .
.
Пример 5.  .
.
Решение. Имеем неопределенность вида  . Разделим числитель и знаменатель на
. Разделим числитель и знаменатель на  (в более общем случае, когда числитель и знаменатель представляют многочлены разных степеней, делят на
(в более общем случае, когда числитель и знаменатель представляют многочлены разных степеней, делят на  с наибольшим показателем степени числителя и знаменателя). Используя свойства пределов, получим:
с наибольшим показателем степени числителя и знаменателя). Используя свойства пределов, получим:
 .
.
Пример 6. 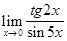 .
.
Решение. При  имеем неопределенность вида
имеем неопределенность вида  . Представим
. Представим 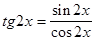 , разделим и умножим числитель и знаменатель на числа 2, 5 и
, разделим и умножим числитель и знаменатель на числа 2, 5 и  , тогда предел преобразуется к виду:
, тогда предел преобразуется к виду:

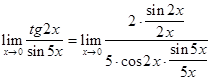 .
.
Пользуясь свойствами пределов и первым замечательным пределом, далее имеем:
 .
.
Пример 7.  .
.
Решение. Имеем неопределенность вида [  ], так как
], так как
 , а
, а  .
.
Выделим у дроби целую часть
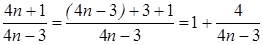 .
.
Введем новую переменную 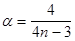 и выразим отсюда
и выразим отсюда  через
через  :
:  . Тогда
. Тогда

Заметим, что при  переменная
переменная  . Теперь, переходя к новой переменной и используя второй замечательный предел, получим:
. Теперь, переходя к новой переменной и используя второй замечательный предел, получим:

= 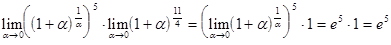 .
.
Неопределенности вида  путем алгебраических преобразований приводятся к виду
путем алгебраических преобразований приводятся к виду  . Неопределенности вида
. Неопределенности вида  ,
,  можно раскрыть, предварительно прологарифмировав соответствующую функцию. Неопределенности вида
можно раскрыть, предварительно прологарифмировав соответствующую функцию. Неопределенности вида  можно исключить, используя правило Лопиталя, которое изложено в конце темы 2.
можно исключить, используя правило Лопиталя, которое изложено в конце темы 2.
Пример 8. Первоначальный вклад в банк составил  денежных единиц. Банк выплачивает ежегодно
денежных единиц. Банк выплачивает ежегодно  % годовых. Необходимо найти размер вклада
% годовых. Необходимо найти размер вклада 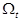 через
через  лет при непрерывном начислении процентов. Решить задачу при
лет при непрерывном начислении процентов. Решить задачу при  =10,
=10,  =5%,
=5%,  =20 лет.
=20 лет.
Решение. При  % годовых размер вклада ежегодно будет увеличиваться в
% годовых размер вклада ежегодно будет увеличиваться в
 раз, т.е.
раз, т.е.  .
.
Если начислять проценты по вкладам не один раз в год, а  раз, то размер вклада за
раз, то размер вклада за  лет при
лет при  начислениях составит
начислениях составит
 .
.
Тогда размер вклада за  лет при непрерывном начислении процентов (
лет при непрерывном начислении процентов ( ) сводится к нахождению предела
) сводится к нахождению предела
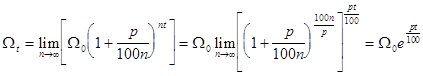 .
.
Здесь при решении использовался второй замечательный предел.
Подставляя исходные числовые данные задачи, получаем
 (ден. единиц).
(ден. единиц).
Вопросы для самопроверки
Дайте определение предела функции в точке.
Назовите основные свойства пределов функций.
Какие виды неопределенностей встречаются при нахождении пределов?
Какие пределы называются замечательными?
Какие функции называют бесконечно малыми?
Задачи для самостоятельной работы
Найти пределы следующих функций:
| Номер варианта | А) | Б) |

| 
| |

| 
| |

| 
| |
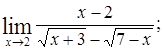
| 
| |

| 
| |

| 
| |

| 
| |

| 
| |
| 
| |

| 
|
Таблица 1.
Тема 2. Производная функции
Приращением функции  в точке
в точке  , соответствующим приращению аргумента
, соответствующим приращению аргумента 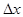 , называется число
, называется число  .
.
Производной функции  в точке
в точке  называется предел отношения приращения функции
называется предел отношения приращения функции  к приращению аргумента
к приращению аргумента 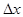 при
при  , если этот предел существует, и обозначается:
, если этот предел существует, и обозначается:
 .
.
Нахождение производной функции называется дифференцированием этой функции. Если функция  имеет в точке
имеет в точке  конечную производную, то функция называется дифференцируемой в этой точке.
конечную производную, то функция называется дифференцируемой в этой точке.
Важнейшими правилами дифференцирования являются следующие.
Производная постоянной  равна нулю:
равна нулю:  .
.
Постоянный множитель выносится за знак производной
 .
.
Производная суммы (разности) функций равна сумме (разности) производных этих функций
 .
.
Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго
 .
.
Производная частного двух дифференцируемых функций находится по формуле
 .
.
Пусть переменная 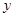 есть функция от переменной
есть функция от переменной  (например,
(например, 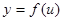 ), а переменная
), а переменная 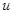 , в свою очередь, есть функция от независимой переменной
, в свою очередь, есть функция от независимой переменной  (
( ), иначе задана сложная функция
), иначе задана сложная функция  .
.
Если 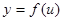 и
и  - дифференцируемые функции от своих аргументов, то производная сложной функции существует и равна производной данной функции по промежуточному аргументу
- дифференцируемые функции от своих аргументов, то производная сложной функции существует и равна производной данной функции по промежуточному аргументу 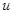 , умноженной на производную самого промежуточного аргумента по независимой переменной
, умноженной на производную самого промежуточного аргумента по независимой переменной 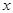 :
:
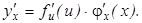
Если функция, производную которой нужно найти, представляет из себя комбинацию элементарных функций, то для вычисления производной применяются правила дифференцирования и таблица производных элементарных функций, приводимая ниже.
Таблица 2.
| № | функция | производная | № | функция | производная |
| 
| 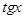
| 1/ 
| ||

| 
| 
| -1/ 
| ||

| 1/ 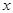
| 
| 1/( ) )
| ||

| 
| 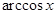
| -1/( ) )
| ||

| 
| 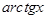
| 1/(1+ 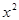 ) )
| ||

| - 
| 
| -1/(1+ 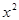 ) )
|
Пример 1. Найти производную функции
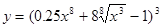 .
.
Решение. Представим ее как сложную функцию. Пусть  , тогда
, тогда  и
и  . Найдем производную по промежуточному аргументу
. Найдем производную по промежуточному аргументу  как степенной функции
как степенной функции
 .
.
В свою очередь, промежуточный аргумент 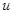 представляется в виде суммы двух степенных функций минус постоянная, поэтому, используя правила 1-3,по-лучим
представляется в виде суммы двух степенных функций минус постоянная, поэтому, используя правила 1-3,по-лучим

= 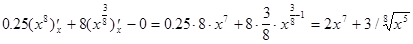 .
.
Отсюда производная искомой функции
 .
.
Пример 2. Найти производную функции
 .
.
Решение. Обозначим  ,
,  . Тогда
. Тогда 
 и искомая производная находится из формулы
и искомая производная находится из формулы  .
.
Производную  находим из таблицы производных элементарных функций
находим из таблицы производных элементарных функций
 .
.
Второй сомножитель 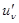 представляет производную от степенной функции
представляет производную от степенной функции

Наконец, последняя производная  находится по правилам дифференцирования частного
находится по правилам дифференцирования частного

=  =
=  .
.
В итоге получаем искомую производную
 .
.
Пример 3. Наити производную
 .
.
Решение. Производная суммы двух функций есть сумма их производных
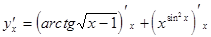 .
.
Для нахождения производной первого слагаемого  обозначим
обозначим  ,
, 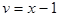 .
.
Тогда  ,
,

= 
Производную второго слагаемого  найдем по правилу дифференцирования степенно-показательной функции. Прологарифмируем функцию
найдем по правилу дифференцирования степенно-показательной функции. Прологарифмируем функцию  :
:  Дифференцируем левую и правую часть полученного равенства
Дифференцируем левую и правую часть полученного равенства

Отсюда

Наконец, находим производную искомой функции
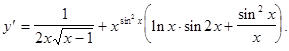
Пример 4. На основе опытных данных построена математическая модель спроса  населения на некоторый товар в зависимости от цены
населения на некоторый товар в зависимости от цены  :
:
 .
.
Определить эластичность спроса при 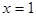 (в условных денежных един.).
(в условных денежных един.).
Решение. Эластичностью спроса  называют предел отношения относительного приращения спроса
называют предел отношения относительного приращения спроса  к относительному приращению цены
к относительному приращению цены  при
при  :
:
 .
.
Если  >1, то спрос называют эластичным, при
>1, то спрос называют эластичным, при  <1 – неэластичным, а при
<1 – неэластичным, а при  нейтральным.
нейтральным.
Найдем производную
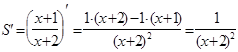 .
.
Тогда
 .
.
Определим эластичность спроса при 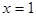 :
:  . Таким образом, при такой цене имеем неэластичный спрос.
. Таким образом, при такой цене имеем неэластичный спрос.
Правило Лопиталя. При нахождении пределов функций (тема 1) неопределенности вида 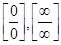 можно исключить, применяя правило Лопиталя: предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных, если последний существует, т. е.
можно исключить, применяя правило Лопиталя: предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных, если последний существует, т. е.

Если  (или
(или  ), то правило Лопиталя можно использовать вторично, т.е.
), то правило Лопиталя можно использовать вторично, т.е.

В общем случае правило Лопиталя можно применять неоднократно.
Пример 5. Найти

Решение. Для раскрытия неопределенности применим правило Лопиталя.

Неопределенность вида  по-прежнему сохраняется. Применим правило Лопиталя еще раз:
по-прежнему сохраняется. Применим правило Лопиталя еще раз:

Вопросы для самопроверки
Дайте определение производной функции в точке.
Какая функция называется дифференцируемой в точке?
Назовите важнейшие правила дифференцирования.
Как находится производная сложной функции?
Сформулируйте правило Лопиталя.
Задачи для самостоятельной работы
Найти производные следующих функций:
Таблица 3.
| Номер варианта | А) | Б) | В) |
| y=(3x4-4x(-1/4)+2)5 | y=arccos2x+(1-4x2)1/2 | y=2tgx+x sin(2x | |
| y=(5x2+4x(5/4)+3)3 | y=arctg(x2-1)1/2 | y=e3x-2x tg(3x) | |
| y=(0.25x8+8x(3/8)-1)3 | y=arccos(1-x2)1/2 | y=3cosx-x sin(2x) | |
| y=(0.2x5-3x(4/3)-4)4 | y=arctg(x-1)1/2 | 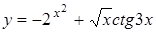
| |
| y=(3x8+5x(2/5)-3)5 | y=arctg(2/(x-3)) | 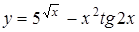
| |
| y=(5x4-2x(-3/2)+3)4 | y=arccos(1-x)1/2 | 
| |
| y=(4x3+3x(-4/3)-2)5 | y=arcctg(x-1)1/2 | 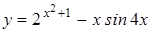
| |
| y=(7x5-3x(5/3)-6)4 | y=arcsin3x-(1-9x2)1/2 | y=etgx-x1/2 cos(2x). | |
| y=(3x4-4x(-1/4)-3)5 | y=arctg(1/(x-1)) | y=x tg3x+2x-2 | |
| y=(8x3-9x(-7/3)+6)5 | y=arcsin((1-x)1/2) | 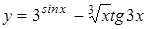
|