Дифференциальным уравнением (ДУ) называют уравнение, связывающее искомую функцию одной или нескольких переменных, эти переменные и производные различных порядков данной функции.
В случае, когда искомая функция зависит от одной переменной, дифференциальное уравнение называется обыкновенным. В общем виде оно записывается:
 . (1)
. (1)
Порядок 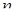 старшей производной искомой функции, входящей в запись уравнения (1), называется порядком дифференциального уравнения.
старшей производной искомой функции, входящей в запись уравнения (1), называется порядком дифференциального уравнения.
Решением уравнения называется такая функция 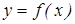 , которая при подстановке ее в уравнение (1) обращает его в тождество. Задача нахождения решения ДУ называется задачей интегрирования данного ДУ, а график решения ДУ называется интегральной кривой.
, которая при подстановке ее в уравнение (1) обращает его в тождество. Задача нахождения решения ДУ называется задачей интегрирования данного ДУ, а график решения ДУ называется интегральной кривой.
Общим решением ДУ вида (1) 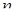 - го порядка называется функция
- го порядка называется функция
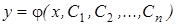 ,
,
где 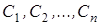 - произвольные постоянные.
- произвольные постоянные.
Частным решением ДУ называется решение, получаемое из общего решения при конкретных числовых значениях постоянных 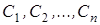 .
.
Дифференциальное уравнение 1-го порядка, разрешенное относительно производной, записывается в общем виде
 . (2)
. (2)
Его общим решением является функция одной произвольной постоянной
 . (3)
. (3)
Для получения однозначного решения требуется задать начальное условие, которое геометрически представляет собой задание точки плоскости, через которую проходит данная интегральная кривая. Например, оно может быть записано в виде
 =const.
=const.
С использованием данного условия общее решение (3) запишется
 ,
,
что позволяет определить из полученного соотношения конкретное значение постоянной  и тем самым получить некоторое частное решение уравнения (2).
и тем самым получить некоторое частное решение уравнения (2).
ДУ 1-го порядка называется уравнением с разделяющимися переменными, если оно может быть представлено в виде
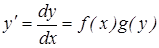 . (4)
. (4)
Для нахождения общего решения такого уравнения его преобразовывают к виду, в котором дифференциал 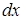 и функция
и функция  окажутся в одной части уравнения, а
окажутся в одной части уравнения, а  и
и 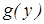 - в другой:
- в другой:
 . (5)
. (5)
Затем интегрируются обе части полученного равенства (с одной общей постоянной)
 .
.
Пример 1. Найти общее решение следующего ДУ:  .
.
Решение. Сначала преобразуем уравнение к виду (4)
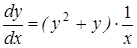 ,
,
а затем к виду (5):
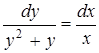 .
.
Найдем интеграл от левой части. Для этого представим подынтегральную функцию в виде следующей суммы
 .
.
Приравнивая числители, получаем
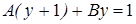 .
.
Найдем из последнего равенства  и
и  , последовательно положив в нем
, последовательно положив в нем 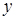 =0 и
=0 и 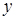 =-1:
=-1:
При 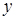 =0 имеем
=0 имеем 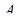 =1, а при
=1, а при 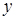 = -1 получаем
= -1 получаем  =-1.
=-1.
Отсюда
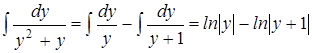 .
.
Интеграл от правой части 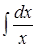 является табличным и равен
является табличным и равен 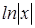 .
.
Запишем произвольную постоянную в виде  .
.
Тогда
 .
.
Отсюда
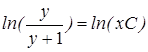 или
или 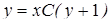 .
.
Разрешая относительно 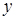 , окончательно получаем общее решение уравнения
, окончательно получаем общее решение уравнения
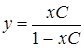 .
.
Дифференциальное уравнение 1-го порядка называется линейным, если оно имеет вид
 . (6)
. (6)
Если  0, то уравнение (6) называют однородным, в противном случае – неоднородным.
0, то уравнение (6) называют однородным, в противном случае – неоднородным.
Один из вариантов решения уравнения (6) сводится к представлению решения в виде произведения двух функций
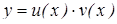 , (7)
, (7)
одна из которых является произвольной, а другая определяется из уравнения (6).
Так как
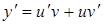 , (8)
, (8)
то подставляя (7) и (8) в уравнение (6), получим:
 . (9)
. (9)
Полагая функцию  произвольной, найдем ее из условия равенства нулю выражения в круглых скобках уравнения (9), т.е. как частное решение уравнения:
произвольной, найдем ее из условия равенства нулю выражения в круглых скобках уравнения (9), т.е. как частное решение уравнения:
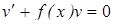 ,
,
которое является уравнением с разделяющимся переменным.
Тогда при определенной  ) можно найти функцию
) можно найти функцию  из оставшейся упрощенной (из-за равенства нулю выражение в круглой скобке) части уравнения (9):
из оставшейся упрощенной (из-за равенства нулю выражение в круглой скобке) части уравнения (9):
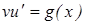 ,
,
которая также является дифференциальным уравнением с разделяющимися переменными. Найденные 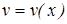 и
и  определяют общее решение
определяют общее решение  исходного дифференциального уравнения.
исходного дифференциального уравнения.
Пример 2.Найти общее и частное решение уравнения  с начальным условием
с начальным условием 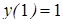 .
.
Решение. Разделим левую и правую часть на  :
:
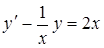 .
.
Получили линейное неоднородное уравнение.
Пусть  , тогда
, тогда 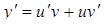 и исходное уравнение примет вид:
и исходное уравнение примет вид:
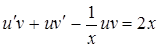 или
или  . (10)
. (10)
Потребуем:
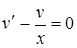 , т.е.
, т.е. 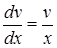 .
.
Отсюда, разделяя переменные

и проинтегрировав
 ,
,
получим общее решение
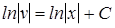
и частное (например, положив 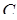 = 0)
= 0)
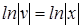 или
или 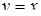 .
.
При 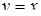 и
и 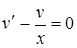 уравнение (10) примет вид:
уравнение (10) примет вид:
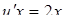 или
или  .
.
Отсюда 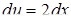 .
.
Интегрируя это уравнение получим:

Окончательно получаем общее решение исходного уравнения:
 .
.
Воспользуемся начальным условием для нахождения требуемого частного решения:

Отсюда 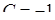 и искомое частное решение имеет вид
и искомое частное решение имеет вид
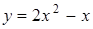 .
.
Вопросы для самопроверки
1. Дайте определения дифференциального уравнения и его решения.
2. Что называют общим и частным решением дифференциального уравнения?
3. Какое ДУ называют уравнением с разделяющимися переменными?
4. Какое ДУ 1-го порядка называют линейным?
5. Опишите общую схему метода решения линейного ДУ 1-го порядка.
Задачи для самостоятельной работы
Найти общее и частное решения дифференциального уравнения первого порядка, используя начальные условия.
Таблица 9.
| Номер варианта | Дифференциальное уравнение | Начальные условия |
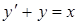
| 
| |
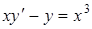
| 
| |

| 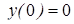
| |
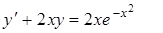
| 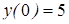
| |
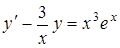
| 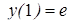
| |

| 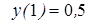
| |
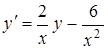
| 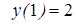
| |
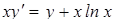
| 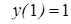
| |

| 
| |

| 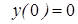
|
Правила выполнения и оформления контрольной работы
1. Выбор вариантов осуществляется в соответствии с последней цифрой учебного шифра студента (например, если последняя цифра «3», то выполняется вариант номер 3, если - «0», то - вариант номер 10).
2. Контрольная работа пишется чернилами любого цвета (кроме красного) в тонкой тетради, для замечаний рецензента оставляются поля. На обложке тетради указывают фамилию, имя, отчество студента, номер студенческой группы, учебный шифр (серия и номер зачетной книжки), название кафедры, наименование дисциплины и номер контрольной работы, а также домашний адрес.
3. Решение задач следует располагать в порядке следования номеров, указанных в задании, сохраняя номера задач. Условия задач выписывать обязательно. Если несколько задач имеют общую формулировку, то при переписывании общие условия заменяют конкретными данными.
4. Решения задач требуется оформлять аккуратно, подробно объясняя все действия и используемые формулы. В конце работы приводится список использованной литературы, указывается дата выполнения работы и ставится подпись исполнителя.
Литература
Высшая математика для экономистов. Под ред. Н.Ш. Кремера. М.: Банки и биржи, 1997.
Математика: Учебное пособие для экономических специальностей. Под ред. Р.Ш. Марданова, Казань: Изд-во КФЭИ, 1999.
Карасев А.И. Курс высшей математики для экономических вузов. М.: Высшая школа, 1982
Кудрявцев В.А. Краткий курс высшей математики. М.: Наука, 1986
Талызин В.А. Контрольная работа по высшей математике. Казань: КИ МГУК, 1998.