5-е занятие. Векторы.
Повторить: понятие вектора в  - мерном пространстве, ранга системы векторов, базы (базиса) и его нахождение.
- мерном пространстве, ранга системы векторов, базы (базиса) и его нахождение.
Пример 1. Вычислить ранг системы векторов:  .
.
Решение. Проведём ЭП с матрицей: 
 . Т.к.
. Т.к.  , то
, то 
 ранг системы векторов равен 3.
ранг системы векторов равен 3.
Пример 2. Найти какую-нибудь базу системы векторов и через неё выразить остальные векторы системы:  .
.
Решение. 1). Вычислим ранг системы векторов:

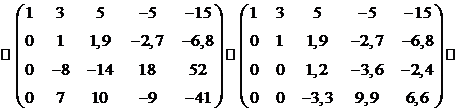



 ранг системы векторов равен 3,
ранг системы векторов равен 3,  любые три вектора из пяти образуют базис. В качестве базиса выберем векторы
любые три вектора из пяти образуют базис. В качестве базиса выберем векторы  . Разложим по этому базису оставшиеся векторы
. Разложим по этому базису оставшиеся векторы  и
и 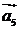 .
.
2).  , где
, где  - некоторые числа, определяемые из системы уравнений:
- некоторые числа, определяемые из системы уравнений:  по методу Гаусса:
по методу Гаусса: 

 т.е. координаты вектора
т.е. координаты вектора  в базисе
в базисе  есть
есть 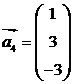 или
или  .
.
3). Аналогично,  , находим
, находим  или
или  .
.
Задания для решения.
1. Вычислить ранги системы векторов:
а).  .
.
б).  .
.
в).  .
.
Ответ: а). 3. б). 3. в). 3.
2. Найти какую-нибудь базу системы векторов и через неё выразить остальные векторы системы:
а).  .
.
б).  .
.
Ответ: а).  . б).
. б).  .
.
3. Векторы  составляют базис пространства. Каковы в этом базисе координаты векторов:
составляют базис пространства. Каковы в этом базисе координаты векторов:
а).  . б).
. б).  . в).
. в).  . г).
. г).  . д).
. д).  ?
?
Ответ: а).  . б).
. б).  . в).
. в).  . г).
. г).  . д).
. д).  .
.
4. Векторы  составляют базис пространства. Можно ли подобрать такие числа
составляют базис пространства. Можно ли подобрать такие числа  , при которых
, при которых  ?
?
Указание. Составить и решить систему уравнений:  .
.
Ответ: да, можно:  .
.
6-е занятие. Векторы. Скалярное произведение.
Повторить: определение и свойства скалярного произведения векторов, определение коллинеарных векторов, угла между двумя векторами, вычисление проекции одного вектора на другой.
Опр. Модулем вектора 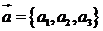 называется его длина:
называется его длина:  .
.
Опр. Скалярным произведением векторов  и
и  называется произведение их модулей на косинус угла между ними:
называется произведение их модулей на косинус угла между ними:  .
.
Угол между векторами  и
и  :
:  ;
;  .
.
Скалярное произведение в координатах: 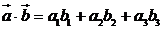 , где
, где 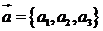 ,
,  .
.
Опр. Коллинеарными называются векторы, которые лежат на одной прямой или на параллельных прямых.
У коллинеарных векторов соответствующие координаты пропорциональны.
Обозначим  - проекция вектора
- проекция вектора  на вектор
на вектор  , тогда
, тогда 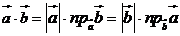 , откуда соответствующие
, откуда соответствующие
проекции вектора на вектор:  ;
;  .
.
Задания для решения.
1. Найти скалярный квадрат вектора: а). 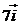 . б).
. б).  . в).
. в). 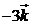 .
.
Указание. Скалярный квадрат вектора 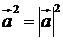 . Ответ: а). 49. б). 36. в). 9.
. Ответ: а). 49. б). 36. в). 9.
2. Даны векторы  и
и  . При каком значении параметра
. При каком значении параметра 
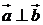 ? Ответ:
? Ответ: 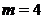 .
.
3. Вычислить угол между прямыми  и
и  , если
, если  ,
, 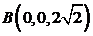 ,
,  ,
, 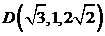 .
.
Указание. Вычислить косинус угла между векторами  и
и  . Ответ:
. Ответ:  .
.
4. Коллинеарны ли векторы 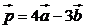 и
и 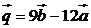 , где
, где  ,
,  ? Ответ: да.
? Ответ: да.
5. Даны точки  ,
,  ,
,  ,
, 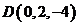 . Определить векторы
. Определить векторы  ,
,  и найти
и найти  . Ответ: -6.
. Ответ: -6.
6. Даны точки  ,
,  ,
, 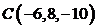 . Найти косинус угла между векторами
. Найти косинус угла между векторами  и
и  . Ответ: -1.
. Ответ: -1.
7. Дан  с вершинами
с вершинами  ,
,  ,
,  . Найти
. Найти  и сделать проверку.
и сделать проверку.
8. Найти скалярное произведение векторов  и
и  , если
, если 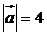 ,
, 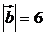 и угол между
и угол между  и
и  равен
равен 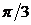 .
.
7-е занятие. Векторы. Векторное и смешанное произведение.
Повторить: определение и свойства векторного и смешанного произведения векторов.
Опр.  , если:
, если:
1).  , где
, где  - угол между
- угол между  и
и  ;
;
2).  и
и  ;
;
3). Векторы  образуют правую тройку.
образуют правую тройку.
Применение: площадь параллелограмма, построенного на векторах  и
и  , вычисляется по формуле:
, вычисляется по формуле:  , площадь треугольника
, площадь треугольника  .
.
Векторное произведение в координатах:  , где
, где 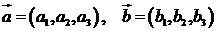 .
.
Опр.  .
.
Применение: объём параллелепипеда, построенного на векторах  ,
,  и
и  :
:  ; объём треугольной призмы:
; объём треугольной призмы:  ; объём треугольной пирамиды:
; объём треугольной пирамиды:  ; условие компланарности:
; условие компланарности:  .
.
Задания для решения.
1. Даны векторы  и
и 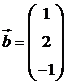 . Найти координаты векторных произведений: а).
. Найти координаты векторных произведений: а).  ; б).
; б).  . Ответ: а).
. Ответ: а).  . б).
. б).  .
.
2. Сила  приложена к точке
приложена к точке  . Найти её момент относительно начала координат. Указание.
. Найти её момент относительно начала координат. Указание.  .
.
3. Даны три силы 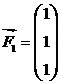 ,
,  ,
,  , приложенные к точке
, приложенные к точке  . Определить момент их равнодействующей относительно точки
. Определить момент их равнодействующей относительно точки 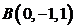 .
.
Указание.  ,
,  . Ответ:
. Ответ:  .
.
4. Вычислить объём треугольной призмы, построенной на векторах
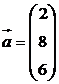 ,
,  ,
, 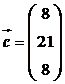 . Ответ: 25.
. Ответ: 25.
5. Вычислить объём параллелепипеда, построенного на векторах  ,
,  ,
,  , и исследовать, какую тройку образуют эти векторы.
, и исследовать, какую тройку образуют эти векторы.
Ответ: 81, правую.
6. Построить пирамиду с вершинами  ,
,  ,
,  и
и  и вычислить её объём, площадь грани
и вычислить её объём, площадь грани  и высоты пирамиды, опущенную на эту грань.
и высоты пирамиды, опущенную на эту грань.
Указание.  , где
, где  . Ответ: 14,
. Ответ: 14, 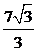 .
.
7. Построить пирамиду с вершинами  ,
,  ,
,  и
и 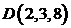 , вычислить её объём и высоту, опущенную на грань
, вычислить её объём и высоту, опущенную на грань  .
.
Ответ: 14,  .
.
8. Вычислить диагонали и площадь параллелограмма, построенного на векторах  и
и  .
.
Решение.  ,
,  ,
,  ,
, 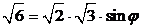

 ,
,  ,
,  .
.
Второй способ:  ;
;  .
.
Ответ:  .
.
8-е занятие. Контрольная работа № 2 по теме «Векторная алгебра».
Примерный вариант контрольной работы.
1. Написать разложение вектора  по векторам
по векторам  ,
,  ,
,  .
.
2. Вычислить объём треугольной пирамиды с вершинами  ,
,  ,
,  и
и  , а также её высоту, опущенную на грань
, а также её высоту, опущенную на грань  .
.
3. Исследовать и решить однородную систему уравнений: 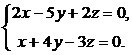
Дополнительные задания по теме «Линейная и векторная алгебра».
1. Вычислить определители:
а).  . б).
. б).  . в).
. в).  . г).
. г).  .
.
Ответ: а). 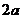 . б). 1. в).
. б). 1. в).  . г). 144.
. г). 144.
2. Найти площадь треугольника с вершинами  .
.
Ответ: 10.
3. Решить системы уравнений:
а). 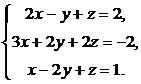 б).
б).  в).
в). 
Ответ: а).  . б).
. б). 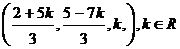 . в). Несовместна.
. в). Несовместна.
4. Определить угол между векторами  и
и  .
.
Ответ:  .
.
5. Даны векторы  и
и  . Определить
. Определить  и
и  .
.
Ответ:  ;
;  .
.
6. Даны три последовательные вершины параллелограмма  ,
,  и
и  . Найти его четвертую вершину
. Найти его четвертую вершину  и угол между векторами
и угол между векторами  и
и  . Ответ:
. Ответ:  ,
,  .
.
7. Определить и построить вектор  , если:
, если:
а).  ,
,  . б).
. б).  ,
,  . в).
. в).  ,
,  . Найти в каждом случае площадь параллелограмма, построенного на векторах
. Найти в каждом случае площадь параллелограмма, построенного на векторах  и
и  .
.
Ответ: а). 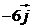 ;
;  . б).
. б). 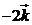 ;
;  . в).
. в).  ;
; 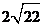 .
.
8. Вычислить площадь параллелограмма и его высоту, построенного на векторах  и
и  . Ответ:
. Ответ:  ;
;  .
.
9. Даны вершины треугольника:  ,
,  ,
,  . Вычислить его площадь и высоту
. Вычислить его площадь и высоту  . Ответ:
. Ответ:  ;
;  .
.
10. Найти смешанное произведение векторов 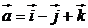 ,
,  ,
,  .
.
11. Показать, что точки  ,
,  ,
, 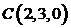 и
и  лежат в одной плоскости.
лежат в одной плоскости.
12. Показать, что векторы  ,
,  ,
, 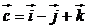 компланарны.
компланарны.
13. Вычислить объём треугольной пирамиды с вершинами  ,
,  ,
, 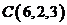 и
и  , а также длину высоты пирамиды, опущенной на грань
, а также длину высоты пирамиды, опущенной на грань  . Ответ:
. Ответ:  ;
;  .
.
Библиография
1. П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова. Высшая математика в упражнениях и задачах. 1 том.
2. Н. С. Пискунов. Дифференциальное и интегральное исчисления. 1 том.
3. Д. Письменный. Конспект лекций по высшей математике.
4. В. С. Шипачёв. Высшая математика.
5. В.П. Минорский Сборник задач по высшей математике.
6. А.А. Шубович, Ю.В. Клочков. Конспект лекций по теме: «Линейная алгебра».
7. А.А. Шубович. Конспект лекций по теме: «Векторная алгебра».
В авторской редакции.
Компьютерная вёрстка Шубовича А.А.
Подписано в печать Формат 
Усл. печ. л. 0,93. Тираж 100. Заказ
Издательско-полиграфический комплекс ВГСХА «Нива»
400002, Волгоград, Университетский пр-т, 26