Раскрытие статической неопределимости

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

МЕХАНИЧЕСКИХ СИСТЕМ

ИСПОЛНИТЕЛЬ ________________ / Барышева А. В. /

студент гр. ФН2-101

 

ПРЕПОДАВАТЕЛЬ ________________ / Яковлев М. Е. /

 

 

Москва 2013

 

Содержание

 

Постановка задачи. 3

1. Степень статической неопределимости. 4

2. Выбор основной системы.. 4

3. Раскрытие статической неопределимости. 5

3.1 Симметричная система. 6

3.2 Кососимметричная система. 7

4. Суммарная эпюра моментов. 9

5. Возникновение пластических деформаций. 9

6. Определение перемещений. 10

Список литературы.. 11

Приложение А……………………………………………………………………………………………………..12

 

Постановка задачи

 

Задание включает схему статически неопределимой пространственной стержневой системы с четырьмя опорами и приложенными равномерно распределенными силами интенсивностью и сосредоточенными силами , где - характерный размер стержневой системы. Схема изображена на рис. 1 (см. Приложение А) в диметрии с искажением расстояния в направлении глубины системы, составляющем на схеме угол с направлениями ширины (горизонталь) и высоты (вертикаль) системы. Глубина системы равна 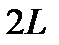. Расстояние между опорами и равно 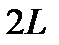. Такое же расстояние между опорами и . Все стержни (с прямоугольной осью и осью в виде дуги окружности радиусом ) выполнены из стальной трубы с наружным диаметром и внутренним диаметром , причем (модуль упругости стали при растяжении , коэффициент Пуассона , предел текучести ). Опоры и 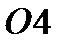- неподвижные шарнирные опоры (НШО), ограничивающие перемещение в трёх направлениях. Опоры и - опоры с жестким защемлением (ОЖЗ), ограничивающие все перемещения и повороты.

Необходимо:

1) установить степень статической неопределимости стержневой системы;

2) выбрать и обосновать основную систему с набором искомых силовых факторов;

3) раскрыть статическую неопределимость исходной стержневой системы;

4) построить суммарную эпюру изгибающих и крутящих моментов;

5) при , и найти значение , при котором хотя бы в одном из стержней возникают пластические деформации;

6) при указанных в п. 5 размерах и найденном значении вычислить вертикальное перемещение заданной на схеме точки и угловое перемещение оси стержня в этой точке в вертикальной плоскости.

 

 

Степень статической неопределимости

Число связей, при котором достигается кинематическая неизменяемость системы, носит название необходимого числа связей. Всякую связь, наложенную сверх необходимых, называют дополнительной. Число дополнительных связей равно степени статической неопределимости системы.

Число внешних связей в системе, изображенной на рис. 1 Приложения А, равно 18. Из них каждой ОЖЗ соответствует 6 связей, а каждой НШО – 3 связи. Кроме того, система содержит замкнутый контур, что приводит к появлению ещё 6 дополнительных внутренних связей. Шесть из этих связей можно определить при помощи уравнений статики. Таким образом, степень статической неопределимости системы равна: 6+6+3+3+6-6=18. Система 6 раз статически неопределима внутренним образом и 12 раз статически неопределима внешним образом.

 

Выбор основной системы

Положим, имеется некоторая симметричная рама. При расчёте таких рам оказывается возможным упростить решение задачи. Под симметричной внешней нагрузкой будем понимать такую, при которой все внешние силы, приложенные к одной части рамы, являются зеркальным отображением сил, приложенных к другой части рамы. Под кососимметричной внешней нагрузкой – такую, при которой силы, приложенные к одной части рамы, также являются зеркальным отображением сил, приложенных к другой части рамы, но противоположны им по знаку.

Если нагрузка, приложенная к симметричной раме, не обладает ни симметричностью, ни кососимметричностью, всегда имеется возможность разложить её на симметричную и кососимметричную. Задача, таким образом, распадается на две.

Аналогично классифицируются и внутренние силовые факторы: два изгибающих момента и нормальная сила – симметричные внутренние силовые факторы, крутящий момент и обе поперечные силы – кососимметричные.

У симметричной рамы в плоскости симметрии при симметричной внешней нагрузке обращаются в нуль кососимметричные силовые факторы, а при кососимметричной нагрузке – симметричные силовые факторы. Стержневая система, изображённая на рис. 1 является симметричной, а внешняя нагрузка не является ни симметричной, ни кососимметричной. Поэтому раскладываем её на две составляющие (Приложение А, рис 2 а, б). Таким образом, задача распадается на две.

Основной системой называют статически определимую, геометрически неизменяемую систему, полученную из заданной путём снятия всех внешних напряжений и дополнительных связей. Эквивалентной системой - основную систему, загруженную внешними напряжениями и неизвестными силовыми факторами взамен отброшенных связей.

Разрежем нашу схему по плоскости симметрии, на местах разреза приложим шесть силовых факторов, опоры с шарнирами заменим тремя силами. Для простоты будем рассматривать только левую половину исходной схемы. На рис. 3а Приложения А приведена эквивалентная система для симметричной задачи, на рис.3б Приложения А для кососимметричной

 

 

Раскрытие статической неопределимости

 

Канонические уравнения метода сил для представленных на рис. 4 систем имеют вид:

(1)

где - вектор искомых силовых факторов; - перемещения в направлении силового фактора под действием силового фактора ; - перемещения в направлении силового фактора под действием внешней нагрузки.

Пренебрегая деформациями растяжения и сдвига, для с помощью интегралов Мора можно записать:

(2)

 

где , , - внутренние моменты, возникающие от -го единичного фактора. - полярный момент инерции сечения, и - моменты инерции сечения. - модуль упругости при растяжении, - модуль сдвига, который находится по формуле ( - коэффициент Пуассона):

В случае, когда стержни выполнены из трубы с наружным диаметром и внутренним диаметром , и соответствующие моменты инерции можно найти по формулам:

(3)

где .

Таким образом, коэффициенты можно получить как результат перемножения эпюр моментов от -го и -го внутренних единичных силовых факторов. Для прямых участков рамы удобно воспользоваться правилом Верещагина. Очевидно, что . Величины определяются перемножением эпюры внешних нагрузок на соответствующие единичные эпюры.

Симметричная система

Приведём эпюры внутренних моментов, вызванных единичными силовыми факторами и внешней нагрузкой, эквивалентной системы для симметричной задачи (см. Приложение А, рис.4а-о).

Обозначим через

Матрица коэффициентов , полученных по формуле (2):

 

 

Вектор-столбец (правая часть уравнения (1)):

Решая систему уравнений (1) при заданных в пункте 4 задания параметрах, получаем искомые силовые факторы :

Таким образом, раскрыта статическая неопределимость симметричной системы.