1. Числовые ряды
Числовым рядом называется сумма вида
,
где числа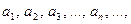 
называемые членами ряда, образуют бесконечную числовую последовательность.
Ряд называется сходящимся, если последовательность его частичных сумм
……………
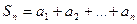
при 
имеет конечный предел 
.
S называется суммой ряда.
Виды числовых рядов
1. 
- гармонический ряд, всегда расходится.
2. 
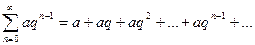- геометрический ряд, который при 
- сходится,
- расходится.
3. 
- обобщенный гармонический ряд, который при 
- расходится,
- сходится.
Необходимый признак сходимости числового ряда
Ряд может сходиться только при условии, что его общий член 
при неограниченном увеличении номера n стремится к нулю:
Если же 
, то ряд расходится – это достаточный признак расходимости ряда.
Пример. Исследовать на сходимость ряд 
.
Найдем 
. Следовательно, ряд расходится.
Достаточные признаки сходимости числового ряда
1. Признак Даламбера
Если для ряда 
существует предел 
, то при 
ряд сходится, при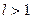 
- ряд расходится (при 
признак Даламбера ответа не дает).
Пример. Исследовать на сходимость ряды:
1) 
.
Для того, чтобы исследовать признак Даламбера найдем 
:
.
Найдем 
.
Так как 
, то ряд сходится.
2) 
.
Найдем 
;
.
Так как 
, следовательно, данный ряд сходится.
2. Признаки сравнения
Имеем числовые ряды: 1) - исследуемый ряд,
2) 
- сходящийся ряд,
3) 
- расходящийся ряд.
2.1. Первый признак сравнения
Если 
, начиная с некоторого номера, то ряд (1) сходится; если 
, то ряд (1) расходится.
2.2. Второй признак сравнения
Если существует конечный и отличный от нуля предел 
, то оба ряда (1) и (2) одновременно сходятся и если 
, то оба ряда (1) и (3) одновременно расходятся.
3. Признак Коши
|
|
Если для ряда существует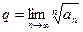 
, то при 
ряд сходится, а при 
- расходится.
Пример. Исследовать на сходимость ряды:
1) 
.
Для определения сходимости ряда используем первый признак сравнения. Возьмем для сравнения геометрический ряд 
, который расходится, т.к. 
.
Так как 
, то исследуемый ряд сходится.
2) 
.
Для определения расходимости ряда используем второй признак сравнения. Возьмем для сравнения гармонический ряд 
, который расходится.
Найдем 
, следовательно, оба ряда одновременно расходятся.
Знакопеременные ряды
Ряд, содержащий как положительные, так и отрицательные члены, называют знакопеременным.
Знакочередующиеся ряды
Знакочередующимся рядом называется ряд вида
, (1)
где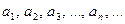 
- положительные члены, у которого любые два стоящие рядом члена имеют противоположные знаки.
Для определения сходимости знакочередующихся рядов применяется достаточный признак сходимости знакочередующихся рядов.
Признак Лейбница
Ряд (1) сходится, если его члены монотонно убывают по абсолютной величине и его общий член стремится к нулю при .
Сходящийся знакочередующийся ряд называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин.
Сходящийся знакочередующийся ряд называется условно сходящимся, если расходится ряд, составленный из абсолютных величин его членов.
Пример. Исследовать на сходимость знакочередующиеся ряды:
1) 
.
Члены данного ряда по абсолютной величине монотонно убывают:
,
и 
.
Следовательно, согласно признаку Лейбница ряд сходится.
Выясним, сходится этот ряд условно или абсолютно.
|
|
Ряд 
, составленный из абсолютных величин членов данного ряда, исследуем на сходимость по второму признаку сравнения. Для сравнения возьмем сходящийся обобщенный гармонический ряд 
.
.
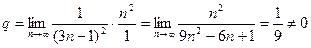Следовательно, ряд - сходится. Поэтому исследуемый ряд сходится абсолютно.
2) 
Члены данного ряда по абсолютной величине монотонно убывают: 
, но 
.
Ряд сходится, т.к. признак Лейбница не выполняется.
3) 
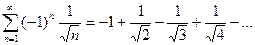
Используя признак Лейбница, получим:
, 
, т.е. ряд сходится.
Рассмотрим ряд, составленный из абсолютных величин членов данного ряда:
.
Это обобщенный гармонический ряд, который расходится, так как 
. Следовательно, данный ряд сходится условно.
Степенные ряды
Степенным рядом называется ряд вида
,
где числа 
называются коэффициентами ряда, а член 
- общим членом ряда.
Областью сходимости степенного ряда называется множество всех значений х, при которых данный ряд сходится.
Число R называется радиусом сходимости ряда, если при 
ряд сходится и притом абсолютно, а при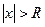 
ряд расходится.
Радиус сходимости R можно найти по формуле
, 
.
Ряд сходится абсолютно на интервале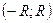 
, который называется интервалом сходимости.
Если 
, то ряд сходится в единственной точке 
.
Если 
, то ряд сходится на интервале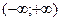 
.
На концах промежутка ряд может сходиться (абсолютно или условно), но может и расходиться. Сходимость ряда при 
исследуется с помощью какого-либо из признаков сходимости.
Примеры. Найти область сходимости ряда.
1) 
.
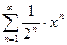Найдем и :
, 
.
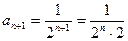Получим 
.
Ряд сходится абсолютно на интервале 
.
При 
имеем ряд 
. Этот ряд расходится, т.к. это геометрический ряд с 
.
|
|
При 
имеем ряд 
. Этот ряд расходится, как геометрический с 
.
Ответ: .
2. 
.
Полагая 
, получим ряд 
. Имеем 
, 
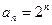и 
.
Получили промежуток абсолютной сходимости y:
.
Заменим у на 
.
, 
.
Исследуем сходимость ряда в точках 
и 
.
При имеем ряд 
, который расходится.
При имеем ряд 
, который расходится.
Ответ: 
.
Разложение функций в степенные ряды
Рядом Тейлора для функции 
называется степенной ряд вида
.
Если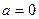 
, то получим частный случай ряда Тейлора:
,
который называется рядом Маклорена.
При решении задач используем разложение в ряд Маклорена функций:
(область сходимости: ),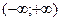
(),
(),
(
),
(
),
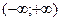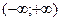Примеры. Найти первых три, отличных от нуля члена разложения в ряд Маклорена функции 
.
1 способ.
Найдем последовательность 
и их значений при .
, 
, 
, 
, 
………………………………………………
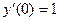
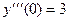
2 способ.
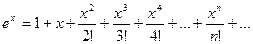
Найдем область сходимости ряда:
, 
и 
.
Ряд сходится на интервале .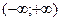
2. Найти первых пять членов разложения в ряд Маклорена функции 
.
.
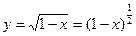Используем разложение в ряд Маклорена:
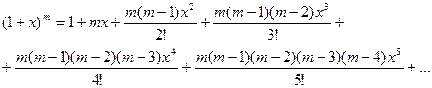Заменяем х на 
и m на 
:
.
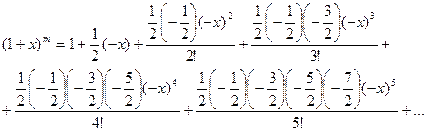
Тригонометрический ряд Фурье
Тригонометрическим рядом Фурье для функции в промежутке изменения аргумента 
называется ряд вида
Функция - периодическая с периодом 
.
Чтобы разложить периодическую функцию с периодом в тригонометрический ряд, нужно найти коэффициенты этого ряда, которые вычисляются по формулам:
;
(n = 1, 2, 3, …);
(n = 1, 2, 3, …).
Пример. Разложить в ряд Фурье функцию
 |
Найдем коэффициенты ряда Фурье:
;
, 
, 
, 
, 
, …
.
, 
, 
, 
, …
Имеем 
.
Функция называется нечетной, если верно равенство: f(-x)= - f(x) и график функции симметричен относительно начала координат О(0;0).
Для нечетной функции коэффициенты
;
;
.
Нечетная функция раскладывается в ряд Фурье по синусам:
Функция называется четной, если верно равенство: f(-x)=f(x) и график функции симметричен относительно оси ОУ.
Для четной функции коэффициенты:
;
;
.
Четная функция раскладывается в ряд Фурье по косинусам:
ЛИТЕРАТУРА
1. Богомолов, Н. В. Практические занятия по математике /
Н. В. Богомолов. - М.: Высшая школа, 1980. – 267 с.
2. Гусак, А. А. Задачи и упражнения по высшей математике.
В 2 ч. Ч. 1 / А. А. Гусак. - Мн.: Высшая школа, 1998. – 167 с.
3. Подольский, В. А. Сборник задач по математике для
техников – программистов: учеб. пособие /
В. А. Подольский. – М.: Высшая школа, 1978. – 240 с.
СОДЕРЖАНИЕ
Введение…………………………………………………………….. 3
Тема VI. Дифференциальные уравнения …………………….…… 4
Тема VII. Числовые и функциональные ряды…………………….. 20
Литература…………………………………………………………... 41