Семантика ППФ.
1) Каждое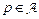 
суть атомарное высказывание. Например, р – «студент спит», q – «слоны живут в Африке»
2) Каждое ППФ образует сложное высказывание, где знаком придаётся смысл логических связок между высказываниями.
– смысл: если А то В (из А следует В).
– смысл: А и В.
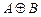– смысл: А или В, но не оба вместе (разделённое или).
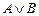– смысл: А или В.
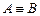– смысл: А тождественно (эквивалентно) В.
ù 
– смысл: не А, другое обозначение – 
Пример: р – студент спит, q – время идёт, r – лекция скучная.
Студент спит, а время идёт ~ 
.
Студент спит, если лекция скучная – 
.
Интерпретация ППФ.
1) Каждому атомарному высказыванию приписывается значение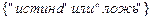 
.
2) Каждой ППФ приписывается значение 
в зависимости от интерпретации связок как знаков операций. Интерпретация связок соответствует таблицам истинности ФАЛ.
| А В | А ® В |
| л л л и и л и и | и и л и |
Например:
3) Если при некоторой интерпретации ППФ истинна, то она называется выполнимой на данной интерпретации.
4) Если ППФ выполнима (истинна) на всех наборах, то она называется тождественно истинной, либо тавтологией, либо общезначимой.
- Другие интерпретации ППФ.
а) Многозначные логики. Например, каждое атомарное высказывание из ППФ и сама ППФ получают значение из множества 
– троичная логика.
б) Правдоподобная логика. Введена Д. Пойа в книге «Математика и правдоподобные рассуждения». ППФ принимают значения из множества 
и интерпретируется как мера правдоподобности высказывания. Д. Пойа ввёл правила для вычисления правдоподобности сложенных высказываний по правдоподобности его составляющих.
III. Специальный вид высказываний – рассуждения или
Умозаключения.
Рассуждение состоит из двух высказываний «p » и «S ». р – высказывание – посылка, S – высказывание – следствие, формальная запись рассуждения – 
читается «из р следует S », или «если Р то S ».Иногда высказывание S ещё называют заключением.
Какими свойствами наделяются правильные рассуждения? Должны соблюдаться следующие отношения:
а) если Р = «истина», то и S должна быть = «истина».
б) если Р = «ложь», то из «лжи» может следовать всё, что угодно, т.е. заключение S может быть и ложным и истинным.
в) из истинной посылки не должно следовать ложное заключение.
Все эти отношения определяют правильные или истинные рассуждения, как это показано в следующей таблице.
| P | S | P/S | P ® S |
| л | л | правильное | И |
| л | и | правильное | И |
| и | л | не правильное | Л |
| и | и | правильное | И |
Можно ввести такую интерпретацию правильного рассуждения: Если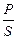 
правильное, то 
и.
Правильно построенное рассуждение является тавтологией. В правильном рассуждении не может быть, чтобы посылка была истинной, а заключение ложным. Эта строка в таблице истинности правильного рассуждения отсутствует. Если 
является тавтологией, то говорят, что рассуждение построено в соответствии с логикой и является логическим законом, который не зависит от интерпретации, а определяется только структурой (ППФ) посылок и следствий.
IV. Логические законы (Аристотель 384–322 д.н.э.).
Впервые в явном виде логические законы, с помощью которых можно строить правильные рассуждения были сформированы Аристотелем. Удивительно, что теория правильных рассуждений, которая называлась силлогистикой и метод вывода правильных заключений из посылок – дедукция были сформированы более 2 тысяч лет тому назад, никем не опровергнуты и считаются присущими человеческому мышлению.
Напомним, что все логические законы должны быть тавтологиями. Иногда законы называются правилами вывода, которые определяют правильный вывод из посылок.
1) Modus ponens (правило отделения) 
; смысл: если верно, что из А следует В и А является истинным, то истинно В.
Формальная запись высказывания (умозаключения, рассуждения) в виде формулы 
. Проверка правильности рассуждения проводится по таблице истинности.
| А В | P | S |
| л л л и и л и и | л л л и | л и л и |
Проверка тавтологии при помощи эквивалентных преобразований.
(А В) & А
 |  |
Пример: Если лекция скучная, то студент спит. Лекция скучная.
Значит: студент спит.
 |
В
2) Modus tollens (отрицательный марус) 
Формальная запись 
;
Пример: 
3) Правило силлогизма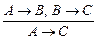 
;
Формула высказывания 
4) Закон контрпозиции 
5) Все соотношения (тождества) алгебры логики суть тавтологии и поэтому являются логическими законами.
6) Закон исключения третьего 
.
7) Закон дистрибутивности 
и 
.
8) Закон «гибельная дилемма» 
Может быть доказана следующая теорема.
Любая формула, которая является тавтологией, может быть приведена к виду и объявлена логическим законом.
Например, 
– есть тавтология, т.к. обозначив
.
Для представления F в форме введём
.