Предприятие выпускает продукцию вида P 1 и P 2, на изготовление которой используется сырье S 1, S 2, S 3. Известны:
b i – запасы сырья; a ij – нормы расхода сырья S i (i =1,2,3) на производство единицы продукции (j =1,2); c j – себестоимость единицы продукции P j; p j – оптовая цена единицы P j.
Определить оптимальный план X =(x 1, x 2) производства продукции P 1 и P 2, при котором при имеющемся количестве сырья можно получить наибольшую прибыль.
Задание
1. Записать числовые данные таблицу и составить математическую модель задачи.
2. Решить задачу графическим методом.
3. Дать экономическое истолкование оптимальному решению и наибольшему значению целевой функции и выяснить, какие виды сырья израсходованы полностью.
4. Определить аналитически и графически, можно ли произвести 3 ед. продукции P 1 и 2 ед. продукции P 2.
Таблица 2.
| Сырье | Продукция | Запасы сырья | |
| P 1 | P 2 | ||
| S 1 | |||
| S 2 | |||
| S 3 | |||
| Себестоимость, cj, ден. ед. | |||
| Оптовая цена, pj, ден. ед. |
Решение
Пусть x 1, x 2, – количество продукции вида P 1 и P 2. Тогда будет израсходовано сырья S 1: x 1+ x 2, сырья S 2: x 2, сырья S 3: x 1. С учетом запасов сырья, система ограничений будет иметь следующий вид
(11)
(12)
Целевая функция (прибыль) будет иметь вид
,
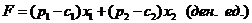или, учитывая данные таблицы,
. (13)
Таким образом, математическая модель задачиформулируется следующим образом:
Требуется найти такой план выпуска продукции X =(x1, x2, x3), удовлетворяющий системе (11) и условиям (12), при которых целевая функция (13) принимает максимальное значение.
Построим многоугольник решений (см. рис. 1). Для этого на плоскости в системе координат x 1O x 2 изобразим граничные прямые: (I) x 1+ x 2=5, (II) x 2=4, (III) 2 x 1+ x 2=8. С учетом условий (12), многоугольник решений будет иметь вид фигуры, заштрихованной на рис. 1. Далее строим линии уровня целевой функции (13). При F =0 линия уровня проходит через начало координат. Затем, например, построим линию уровня F =4, т.е. x 1+2 x 2=4. Ее расположение указывает на направление возрастания целевой функции (градиент целевой функции, вектор 
). Двигая линию уровня, т.е. прямую, целевой функции в направлении вектора , найдем ее самое крайнее положение, при котором она проходит через точку B. Таким образом, оптимальное решение задачи будет находиться в угловой точке B, находящейся на пересечении прямых (I) и (II), т.е. координаты точки B определяются решение системы уравнений
|
|
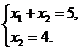
Отсюда находим, что x 1=1, x 2=4, т.е. B (1;4). Максимальное значение целевой функции равно Fmax =1+2×4=9.
Итак, Fmax=9 при оптимальном решении x1=1, x2=4, т.е. максимальная прибыль в 9 ден. ед. может быть достигнута при производстве 1 ед. продукции П 1 и производстве 4 ед. продукции П 2.
Отметим, что при найденном оптимальном плане, сырье S 1 и S 2 расходуются полностью.
Можно ли произвести 3 ед. продукции P 1 и 2 ед. продукции P 2? Да, можно. Поскольку при x 1=3 и x 2=2 все три неравенства выполняются
то такой план является допустимым, но не является оптимальным. На графике (см. рис.1) предложенному плану соответствует точка C (3;2), которая входит в многоугольник допустимых решений, но отличается от оптимального решения, т.е. от точки B.
Задача №3. Симплексный метод решения задачи линейного
программирования
Условие задачи №3