1) Из элементов электрической цепи: конденсатора, резистора и катушки индуктивности собрать Т-образный (нечетный номер бригады) или П-образный (четный номер бригады) четырехполюсник и включить его по схеме, представленной на рис. 5.3.
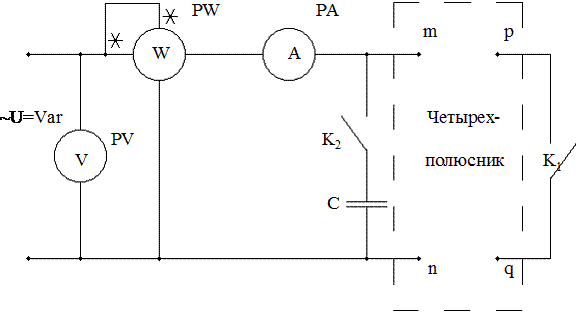
Рисунок 5.3 – Электрическая схема определения параметров четырехполюсника
Примечание. Расположение элементов в четырехполюснике определяет для бригады преподаватель.
2) Выполнить опыты холостого хода и короткого замыкания при питании четырехполюсника со стороны зажимов m-n. Результаты занести в табл. 5.1.
Примечания:
1. Напряжение на входе устанавливать плавно, идя от нуля, и такое, чтобы показания приборов были удобны для снятия результатов.
2. Для определения знака аргумента комплексных сопротивлений замыкают ключ K2. При этом, если показание амперметра уменьшится, то знак «плюс», а если увеличится, то знак «минус».
Таблица 5.1 – Результаты опытов х.х и к.з. четырехполюсника
| Питание со стороны зажимов | Опыт | Измерено | Вычислено | |||
| U | I | P | знак φ | Комплексное сопротивление | ||
| m–n | х.х. | Z10 = | ||||
| m–n | к.з. | Z1K = | ||||
| p–q | х.х. | Z20 = | ||||
| p–q | к.з. | Z2K = |
3) Выполнить опыты холостого хода и короткого замыкания при подаче энергии со стороны зажимов p–q. Использовать те же приборы и рекомендации, что в п. 2. Полученные данные занести в табл. 5.1.
Обработка результатов измерений
1) Рассчитать параметры, указанные в графе «Вычислено» табл. 5.1. Убедится в справедливости соотношений Z10/Z20 = Z1K/Z2K.
2) Используя вычисленные данные табл. 5.1, определить коэффициенты четырехполюсника А-формы записи уравнений по формулам (5.5) (Т-образный четырехполюсник), (5.6) (П-образный четырехполюсник). Результаты записать в табл. 5.2.
|
|
3) Вычислить параметры исследуемого четырехполюсника (Т-схема нечетная бригада; П-схема – четная бригада). Результаты записать в табл. 5.2.
4) По определенным коэффициентам А-формы записи уравнений или параметрам опытов холостого хода и короткого замыкания исследуемого четырехполюсника определить параметры П-схемы замещения (если исследуемый четырехполюсник Т-схема) или Т-схемы замещения (если исследуемый четырехполюсник П-схема) четырехполюсника. Результаты записать в табл. 5.2.
Таблица 5.2 – Коэффициенты и параметры четырехполюсника
| A | B | C | D | Z1 | Z2 | Z3 | Y1 | Y2 | Y3 |
5) По формулам (5.8) и (5.9) вычислить характеристические сопротивления и постоянную передачи четырехполюсника.
6) Считая, что исследуемый четырехполюсник нагружен на характеристическое сопротивление ZC2, и зная параметры четырехполюсника, определить токи и напряжения на элементах четырехполюсника, если U1 = n·50 В (n – номер бригады).
7) По результатам исследований сделать выводы.
5.5 Контрольные вопросы
1) Что такое четырехполюсник, активный, пассивный четырехполюсник?
2) Привести примеры реальных электрических схем, которые можно рассматривать как четырехполюсники.
3) Какой четырехполюсник называется симметричным?
4) Какими схемами замещения может быть представлен любой реальный четырехполюсник?
Записать уравнения четырехполюсника в А-форме.
Записать уравнения связи коэффициентов А-формы записи.
|
|
Из каких опытов можно найти коэффициенты уравнений четырехполюсника?
Записать уравнения четырехполюсника при холодном ходе.
Записать уравнения четырехполюсника при коротком замыкании выходных зажимов.
Записать выражения для характеристических сопротивлений и постоянной передачи. Объяснить их физический смысл.
Лабораторная работа № 13
Исследование электрических цепей несинусоидального тока
Цель работы – исследование линейных электрических цепей с несинусоидальными источниками питания.
Основные положения
Анализ электрических цепей с несинусоидальными периодическими источниками питания, как правило, осуществляется путем разложения кривых эдс, напряжений или токов в ряд Фурье:
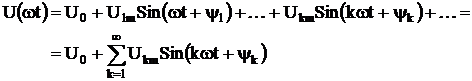(6.1)
Первый член ряда называется постоянной составляющей (нулевой гармоникой), остальные члены ряда соответственно – первой, второй и т.д. гармониками.
Подавляющее большинство функций времени, встречающихся в электротехнике, можно разделить на три основных группы:
– Функции, удовлетворяющие условию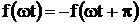 
(симметричные относительно оси абсцисс). Они раскладываются в ряд, который не содержит четных гармоник и постоянной составляющей
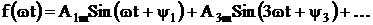(6.2)
– Функции, удовлетворяющие условию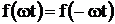 
(симметричные относительно оси ординат). В этом случае ряд не содержит синусов, а только косинусоидальные гармоники.
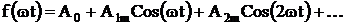(6.3)
– Функции, удовлетворяющие условию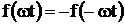 
(симметричные относительно начала координат). Они раскладываются в ряд, не содержащий постоянной составляющей и косинусов:
|
|
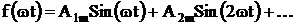(6.4)
Расчет токов и напряжений при воздействии несинусоидальных эдс производится для каждой гармоники отдельно. При расчете необходимо учитывать, что емкостное и индуктивное сопротивление зависят от частоты: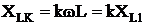 
, 
.
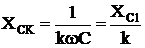Действующие значения несинусоидальных токов, напряжений, эдс (показывают приборы электромагнитной, электродинамической, тепловой систем) определяются согласно выражения:
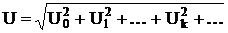, (6.5)
где U1, U2, …, Uk – действующие значения соответствующих гармоник.
Активная мощность в цепях несинусоидального тока равна
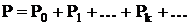, (6.6)
где P0 = U0·I0 – мощность постоянной составляющей;
PK = UK·IK·Cos φK – активная мощность k-гармоники.
Полная мощность электрической цепи несинусоидального тока определяется
S = U·I, (6.7)
где U и I – действующие значения несинусоидального напряжения и несинусоидального тока.
Векторные диаграммы строятся отдельно для каждой гармоники.