1) Собрать цепь по схеме рис. 7.5 для исследования переходного режима в цепях R – C, R – L, R – L – C при питании от источника постоянного напряжения (короткое замыкание цепей).
Формирователь прямоугольных импульсов (ФПИ), выполненный на резисторе Rб и стабилитроны VD, подключить к источнику переменного напряжения ~ 0 – 30 В.
2) Закоротить зажимы 1 – 2. В результате чего получается цепь R – C для исследования заряда – разряда конденсатора через резистор.
3) Зарисовать кривые UC(t), наблюдаемые на экране осциллографа для трех значений сопротивления R при фиксированной емкости C (величина задается преподавателем).
4) По осциллограммам UC(t) определить постоянные времени цепи заряда и разряда конденсатора.
5) По найденным постоянным времени τ рассчитать величины соответствующих сопротивлений.
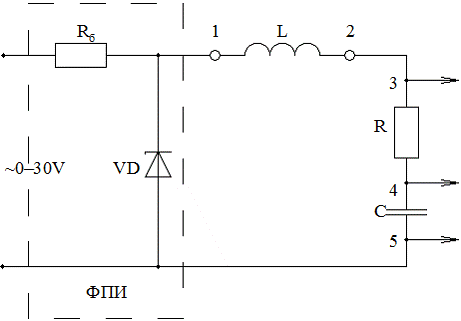
Рисунок 7.5 – Электрическая схема исследования переходных процессов
6) Рассчитать зависимость UC(t) при заряде конденсатора для одного из значений сопротивления (C и U0 принять равным их значениям в эксперименте). Результат занести в табл. 7.1.
Таблица 7.1 – Результаты расчета переходного процесса в цепи R – C
| t | мкс | ||||||
| UC(t) | В |
Полученную кривую сравнить с осциллограммой.
7) Закоротить зажимы 4 – 5 (зажимы 1 – 2 – разомкнуть) в цепи (рис. 7.5). В результате чего получается цепь R – L для исследования переходных режимов.
8) Зарисовать кривые UR(t) 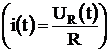 для трех значений сопротивления (задаются преподавателем).
для трех значений сопротивления (задаются преподавателем).
9) По осциллограммам определить постоянные времени цепи R – L (при различных R).
10) По найденным постоянным времени τ рассчитать величины L и Rк.
11) Рассчитать зависимость UR(t) при включении R – L для одного из значений сопротивления R (L и U0 принять равными их значениям в эксперименте). Результаты занести в табл. 7.2.
Таблица 7.2 – Результаты расчета переходных процессов в цепи R – L
| t | мкс | ||||||
| UR(t) | В |
Полученную кривую сравнить с осциллограммой.
12) Снять закоротку с зажимов 4 – 5 (рис. 7.5), получив цепь для исследования переходных процессов в цепи R – L – C.
13) Изменяя величину R резистора и емкость C конденсатора установить колебательный процесс изменения напряжения на конденсаторе и зарисовать его.
14) По осциллограмме UC(t) определить период TC и частоту fC собственных колебаний цепи, а также декремент и логарифмический декремент затухания ln∆.
15) По значениям TC и ln∆ определить значения сопротивлений R1 = Rк + R (Rк – сопротивление катушки индуктивности).
16) Изменяя R резистора установить на экране осциллографа апериодический (критический) переходный процесс. Зарисовать осциллограмму.
17) По результатам исследования сделать вывод.
7.4 Контрольные вопросы и задачи
1) Что такое постоянная времени цепи? Как она вычисляется? Как влияет ее величина на переходный процесс?
2) Могут ли напряжения на конденсаторе и ток через конденсатор изменяться скачками?
3) Как по кривой переходной величины определить постоянную времени?
4) Чему будет равен ток в цепи с последовательным соединением конденсатора емкостью 1 мкФ и резистора с сопротивлением 1 мОм, подключенной к источнику постоянного напряжения U = 100 В, через 1 с после подключения?
5) Что такое декремент затухание и логарифмический декремент затухания? Как они определяются?
6) Определить емкость конденсатора, который за 2 секунды через сопротивление 3 кОм зарядился до 98% напряжения источника.
7) Объясните энергетический процесс в колебательном контуре. Почему при 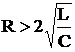 не возникают колебания?
не возникают колебания?
8) Приведите примеры, когда на практике используется явление заряда или разряда конденсатора.
9) Конденсатор емкостью С разряжается на резистор с сопротивлением R = 2 кОм индуктивную катушку с индуктивностью L = 36 мкФ. Какова должна быть наименьшая емкость конденсатора, чтобы его разряд на катушку имел апериодический характер?
10) Определить, за сколько секунд разрядится конденсатор емкостью 0,1 мкФ на сопротивление 10 Ом.