Свойства степеней с рациональными показателями

Степень с дробным показателем мы определяли, распространяя на нее свойства степени с целым показателем. Иными словами, степени с дробными показателями обладают теми же свойствами, что и степени с целыми показателями. А именно:

1. свойство произведения степеней с одинаковыми основаниями 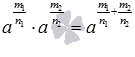при a>0, а есл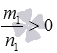и и 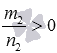, то при a≥0;

2. свойство частного степеней с одинаковыми основаниями 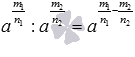при a>0;

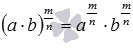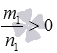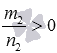3. свойство произведения в дробной степени при a>0 и b>0, а если и , то при a≥0 и (или) b≥0;

4. свойство частного в дробной степени 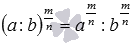при a>0 и b>0, а если 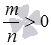, то при a≥0 и b>0;

5. свойство степени в степени 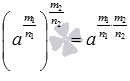при a>0, а есл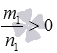и и 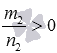, то при a≥0;

6. свойство сравнения степеней с равными рациональными показателями: для любых положительных чисел a и b, a<b и рациональном p при p>0 справедливо неравенство a^p<b^p, а при p<0 – неравенство a^p>b^p;

7. свойство сравнения степеней с рациональными показателями и равными основаниями: для рациональных чисел p и q, p>q при 0<a<1 выполняется неравенство a^p<a^q, а при a>0 – неравенство a^p>a^q.

Доказательство свойств степеней с дробными показателями базируется на определении степени с дробным показателем, на свойствах арифметического корня n-ой степени и на свойствах степени с целым показателем. Приведем доказательства.

По определению степени с дробным показателем 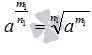и 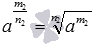, тогда 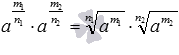. Свойства арифметического корня позволяют нам записать следующие равенства 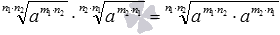. Дальше, используя свойство степени с целым показателем, получаем 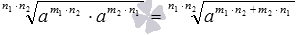, откуда по определению степени с дробным показателем имеем 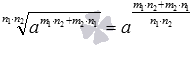, а показатель полученной степени можно преобразовать так: 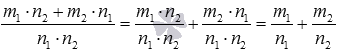. На этом доказательство завершено.

Абсолютно аналогично доказывается второе свойство степеней с дробными показателями:

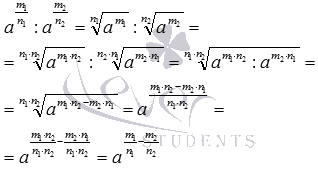
По схожим принципам доказываются и остальные равенства:

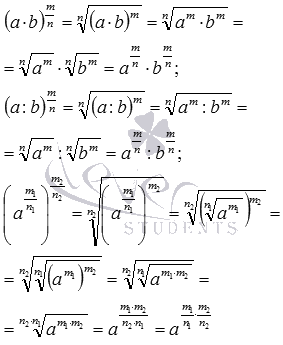
Переходим к доказательству следующего свойства. Докажем, что для любых положительных a и b, a<b и рациональном p при p>0 справедливо неравенство a^p<b^p, а при p<0 – неравенство a^p>b^p. Запишем рациональное число p как m/n, где m – целое число, а n – натуральное. Условиям p<0 и p>0 в этом случае будут эквивалентны условия m<0 и m>0 соответственно. При m>0 и a<b по свойству степени с целым положительным показателем должно выполняться неравенство a^m<b^m. Из этого неравенства по свойству корней имеем 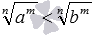, а так как a и b – положительные числа, то на основе определения степени с дробным показателем полученное неравенство можно переписать как 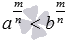, то есть, a^p<b^p.

Аналогично, при m<0 имеем a^m>b^m, откуда 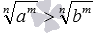, то есть, 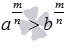и a^p>b^p.

Осталось доказать последнее из перечисленных свойств. Докажем, что для рациональных чисел p и q, p>q при 0<a<1 выполняется неравенство a^p<a^q, а при a>0 – неравенство a^p>a^q. Мы всегда можем привести к общему знаменателю рациональные числа p и q, пусть при этом мы получим обыкновенные дроб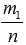и и 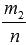, где m₁ и m₂ – целые числа, а n - натуральное. При этом условию p>q будет соответствовать условие m₁>m₂, что следует из правила сравнения обыкновенных дробей с одинаковыми знаменателями. Тогда по свойству сравнения степеней с одинаковыми основаниями и натуральными показателями при 0<a<1 должно быть справедливо неравенство a^m₁<a^m₂, а при a>1 – неравенство a^m₁>a^m₂. Эти неравенства по свойствам корней можно переписать соответственно как 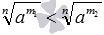и 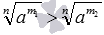. А определение степени с рациональным показателем позволяет перейти к неравенствам 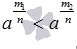и 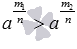соответственно. Отсюда делаем окончательный вывод: при p>q и 0<a<1 выполняется неравенство a^p<a^q, а при a>0 – неравенство a^p>a^q.