Глоссарий
По теме:
«Теорема Пифагора»
Выполнил:
Небыков С.А
Студент ВГСПУ
Гр. МИФ-МБz-21
Учебная практика, 2018 г.
Содержание
Теорема..................................................................................... 3
Доказательства:....…………………………………….
Доказательство через подобные треугольники ….... 4
Доказательство через равнодополняемость............... 5
Доказательство Евклида …………………………….. 6
Доказательство Леонардо да Винчи ………………... 7
Источники …………………………………………….
Теорема

Основная формулировка содержит алгебраические действия — в прямоугольном треугольнике, длины катетов которого равны {\displaystyle a}и {\displaystyle b}, а длина гипотенузы — {\displaystyle c}, выполнено соотношение:
a2 + b2 = c2
Возможна и эквивалентная геометрическая формулировка, прибегающая к понятию площади фигуры: в прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах. В таком виде теорема сформулирована в Началах Евклида.
Обратная теорема Пифагора — утверждение о прямоугольности всякого треугольника, длины сторон которого связаны соотношением a2 + b2 = c2. Как следствие, для всякой тройки положительных чисел a {\displaystyle a}, {\displaystyle b}b и {\displaystyle c}c, такой, что a2 + b2 = c2, существует прямоугольный треугольник с катетами a {\displaystyle a} и {\displaystyle b}b и гипотенузой c {\displaystyle c}.
Доказательства:
Доказательство через подобные треугольники.

Одним из наиболее популярных в учебной литературе доказательств алгебраической формулировки является доказательство с использованием техники подобия треугольников, при этом оно почти непосредственно выводится из аксиом и не задействует понятие площади фигуры.
В нём для треугольника ABC с прямым углом при вершине C со сторонами a, b, c, противолежащими вершинам A, B, C, соответственно, проводится высота CH, при этом (согласно признаку подобия по равенству двух углов) возникают соотношения подобия: треугольник ABC подобен треугольнику ACH и треугольник АВС подобен CBH, из чего непосредственно следуют соотношения:

Получаем
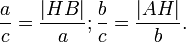
Что эквивалентно

Сложив, получаем

Или 
Доказательство через равнодополняемость

1. Расположим четыре равных прямоугольных треугольника так, как показано на рисунке.
2. 2. Четырёхугольник со сторонами c является квадратом, так как сумма двух острых углов 90°, а развёрнутый угол — 180°.
3. 3. Площадь всей фигуры равна, с одной стороны, площади квадрата со стороной (a+b), а с другой стороны, сумме площадей четырёх треугольников и внутреннего квадрата.
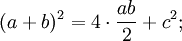

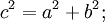
Что и требовалось доказать.
Доказательство Евклида

Идея доказательства Евклида состоит в следующем: попробуем доказать, что половина площади квадрата, построенного на гипотенузе, равна сумме половин площадей квадратов, построенных на катетах, а тогда и площади большого и двух малых квадратов равны. Рассмотрим чертеж слева. На нём мы построили квадраты на сторонах прямоугольного треугольника и провели из вершины прямого угла С луч s перпендикулярно гипотенузе AB, он рассекает квадрат ABIK, построенный на гипотенузе, на два прямоугольника — BHJI и HAKJ соответственно. Оказывается, что площади данных прямоугольников в точности равны площадям квадратов, построенных на соответствующих катетах. Попытаемся доказать, что площадь квадрата DECA равна площади прямоугольника AHJK Для этого воспользуемся вспомогательным наблюдением: Площадь треугольника с той же высотой и основанием, что и данный прямоугольник, равна половине площади заданного прямоугольника. Это следствие определения площади треугольника как половины произведения основания на высоту. Из этого наблюдения вытекает, что площадь треугольника ACK равна площади треугольника AHK (не изображённого на рисунке), которая, в свою очередь, равна половине площади прямоугольника AHJK. Докажем теперь, что площадь треугольника ACK также равна половине площади квадрата DECA. Единственное, что необходимо для этого сделать, — это доказать равенство треугольников ACK и BDA (так как площадь треугольника BDA равна половине площади квадрата по указанному выше свойству). Равенство это очевидно, треугольники равны по двум сторонам и углу между ними. Именно — AB=AK,AD=AC — равенство углов CAK и BAD легко доказать методом движения: повернём треугольник CAK на 90° против часовой стрелки, тогда очевидно, что соответствующие стороны двух рассматриваемых треугольников совпадут (ввиду того, что угол при вершине квадрата — 90°). Рассуждение о равенстве площадей квадрата BCFG и прямоугольника BHJI совершенно аналогично. Тем самым мы доказали, что площадь квадрата, построенного на гипотенузе, слагается из площадей квадратов, построенных на катетах.
Доказательство Леонардо Да Винчи

Главные элементы доказательства — симметрия и движение.
Рассмотрим чертёж, как видно из симметрии, отрезок CI рассекает квадрат ABHJ на две одинаковые части (так как треугольники ABC и JHI равны по построению). Пользуясь поворотом на 90 градусов против часовой стрелки, мы усматриваем равенство заштрихованных фигур CAJI и GDAB. Теперь ясно, что площадь заштрихованной нами фигуры равна сумме половин площадей квадратов, построенных на катетах, и площади исходного треугольника. С другой стороны, она равна половине площади квадрата, построенного на гипотенузе, плюс площадь исходного треугольника.
Источники: