В приведенных выше формулах для нахождения числа размещений и сочетаний предполагалось, что все выбираемые 
элементов различны. Если выбираемые элементы могут повторяться, то говорят о соединениях с повторениями.
Число размещений с повторениями 
.
Число сочетаний с повторениями 
.
Если среди 
элементов есть 
элементов одного вида, 
элементов другого вида и т.д., то число перестановок с повторениями 
, где 
.
Пример 5. Сколько различных четырехзначных чисел можно составить из цифр 5, 6, 7, если цифры в числе могут повторяться?
По условию задачи, цифры в числе могут повторяться, значит речь идет о комбинациях с повторениями. Числа различаются не только составом цифр, но и порядком их расположения (например, числа 5567 и 6575 состоят из одних и тех цифр, записанных в разном порядке). Следовательно, таких чисел будет 
.
Пример 6. В продажу поступили открытки 15 разных видов. Сколькими способами можно образовать набор из 8 открыток, если в него могут войти одинаковые открытки?
Так как виды открыток в наборе могут повторяться, а сами наборы отличаются один от другого только своим составом (очевидно, что расположение открыток в наборе не имеет значения), то число таких наборов равно
.
Пример 7. Сколько различных «слов» (не обязательно имеющих смысл) можно образовать, переставляя буквы в слове КОЛОКОЛ?
В слове КОЛОКОЛ, состоящем из 7 букв, буква К встречается два раза, буква О – три раза, буква Л – два раза, то есть 
, 
, 
, 
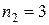. Следовательно, число «слов» равно
.
Свойства числа сочетаний. Треугольник Паскаля. Бином Ньютона
Для любых целых неотрицательных чисел n и k (
) выполняются свойства:
1. 
;
2. 
.
Для того чтобы свойство 2 было справедливо при 
, полагают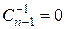 
, поскольку должно выполняться равенство 
и при этом 
.
Свойство 2 позволяет вычислять значения 
, зная 
и 
. Пользуясь этим свойством, можно последовательно вычислить сначала при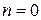 
, затем при 
, при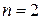 
и т.д. Вычисления удобно располагать в виде следующей треугольной таблицы:
| ||||||||||
| 
| |||||||||
| 
| 
| ||||||||
| 
| 
| 
| |||||||
| 
| 
| 
| 
| ||||||
| 
| 
| 
| 
| 
| |||||
| … | … | … | … | … | … | … | … | … | … | … |
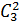
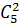
Так как 
, то все числа, стоящие «по краям» треугольной таблицы, равны 1. Каждое же число , расположенное «внутри» треугольной таблицы, равно сумме двух чисел предыдущей строки, стоящих слева и справа от него.
Таким образом, указанную таблицу легко запомнить и восстановить, не пользуясь формулой числа сочетаний:
| ||||||||||
|
|
| |||||||||
|
| 
|
| ||||||||
|
| 
|
|
| |||||||
|
| 
| 
|
|
| ||||||
|
| 
| 
|
|
|
| |||||
| … | … | … | … | … | … | … | … | … | … | … |
Эта таблица называется арифметический треугольник или треугольник Паскаля.
Рассмотрим одну из возможностей применения треугольника Паскаля. Обобщением известных из школьного курса математики формул квадрата и куба суммы (разности) является бином Ньютона:
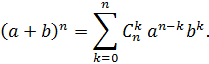
В частности:
Нетрудно заметить, что числовые коэффициенты слагаемых, стоящих в правой части бинома Ньютона, равны числам, стоящим в соответствующей данному числу n строке треугольника Паскаля.
Пример 8. Используя бином Ньютона и треугольник Паскаля, легко получить формулы:
