Глава 2. Модель парной регрессии
В модели парной линейной регрессии зависимость между переменными в генеральной совокупности представляется в виде:
(2.1)
где X – неслучайная величина, а Y и e – случайные величины.
Величина Y называется объясняемой (зависимой) переменной, а X – объясняющей (независимой) переменной. Постоянные a, b – параметры уравнения.
Наличие случайного члена e (ошибки регрессии) связано с воздействием на зависимую переменную других неучтенных в уравнении факторов.
На основе выборочного наблюдения оценивается выборочное уравнение регрессии (линия регрессии):
, 
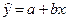(2.2)
где ( а; b) – оценки параметров (a; b).
Метод наименьших квадратов
Рассмотрим задачу «наилучшей» аппроксимации набора наблюдений 
линейным уравнением (2.2).
На рис. 8 приведены диаграмма рассеяния наблюдений и график линии регрессии.
Рис. 8
Величина 
описывается как расчетное значение переменной yi, соответствующее xi. Наблюдаемые значения yi не лежат в точности на линии регрессии, то есть не совпадают с 
.
Определим остаток ei в i -ом наблюдении как разность между фактическим и расчетным значениями зависимой переменной, т.е.
.
Неизвестные значения ( a; b) определяются методом наименьших квадратов (МНК).
Сущность МНК заключается в минимизации суммы квадратов остатков:
.
Здесь (хi, yi) – известные значения (числа), (а; b) – неизвестные.
Запишем необходимые условия экстремума:
.
После преобразования получим следующую систему нормальных уравнений:
.
Решение системы:
(2.3)
Линия регрессии (расчетное значение зависимой переменной):
, или 
.
Линия регрессии проходит через точку 
и выполняются равенства:
.
Коэффициент b есть угловой коэффициент регрессии и показывает, на сколько единиц в среднем изменяется переменная y при увеличении независимой переменной x на единицу.
|
|
Постоянная a дает прогнозируемое значение зависимой переменной при x = 0. Это может иметь смысл в зависимости от того, как далеко находится x = 0 от выборочных значений x.
Можно показать, что
,
где r – коэффициент корреляции между x, y, а sx, sy – их стандартные отклонения.
Если коэффициент r уже рассчитан, то можно получить коэффициенты (a, b) парной регрессии.
После построения уравнения регрессии наблюдаемые значения y находим по:
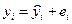. (2.4)
Остатки ei, как и ошибки ei являются случайными величинами, однако они, в отличие от ошибок ei, наблюдаемы.
Докажем, что 
.
Действительно, используя равенства
,
получим
.
Определим выборочные дисперсии величин 
:
– дисперсия наблюдаемых значений y;
– дисперсия расчетных значений ;
– дисперсия остатков e.
Анализ вариации зависимой переменной
Цель регрессионного анализа состоит в объяснении поведения зависимой переменной y.
Пусть на основе выборочных наблюдений построено уравнение регрессии 
, тогда значение зависимой переменной y в каждом наблюдении можно разложить на две составляющие: 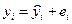, где остаток ei есть та часть зависимой переменной y, которую невозможно объяснить с помощью уравнения регрессии.
Разброс наблюдаемых значений зависимой переменной характеризуется выборочной дисперсией var (y).
Разложим дисперсию var (y):
Поскольку 
то
Таким образом, разложили дисперсию var (y) на две части:
– часть, объясненную регрессионным уравнением;
– необъясненную часть.
|
|
Коэффициентом детерминации R 2 называется отношение
, 
,
характеризующее долю вариации (разброса) зависимой переменной, объясненную с помощью уравнения регрессии.
Отношение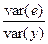 
представляет собой долю необъясненной дисперсии.
Если R 2 = 1, то это означает точную подгонку:
,
т.е. все точки наблюдения лежат на регрессионной прямой.
Если R 2 = 0, то регрессия ничего не дает:
,
т.е. переменная x не улучшает качества предсказания y по сравнению с горизонтальной прямой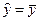 
.
Чем ближе к единице R 2, тем лучше качество подгонки, и более точно аппроксимирует y.
Замечание. Вычисление R 2 корректно, если константа a включена в уравнение регрессии; при этом справедливо разложение 
.
Пример 2.1. Покажем, что 
, где 
коэффициент корреляции между и y.
Действительно, учитывая соотношение:
, получим
Пример 2.2. Покажем, что 
в случае парной регрессии .
Действительно, из соотношений:
имеем: 
.
Вывод. В случае парной регрессии коэффициент детерминации есть квадрат коэффициента корреляции переменных x и y, т.е. R 2 = r 2 x,y.
Пример 2.3. Зависимость переменной в регрессии 
разбивается на две компоненты: 
.
Рассмотрим две регрессии для компонент:
,
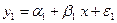Докажем следующие соотношения для МНК-оценок параметров трех регрессий: a=a1+a 2, b=b 1+ b 2. Действительно,
Пример 2.4. Покажем, что если все значения переменных изменить на одно и то же число или в одно и то же число раз, то величина коэффициента b в парной регрессии не изменится.
Пусть 
, тогда
.
Пусть 
, тогда
F -тест на качество оценивания
Для определения статистической значимости коэффициента детерминации R 2 проверяется гипотеза H 0: R 2 = 0 для F -статистики, рассчитываемой по формуле:
|
|
.
Величина F имеет распределение Фишера с n 1 = 1, n 2 = n – 2 степенями свободы.
Проверку значимости R 2 можно произвести двумя способами.
1. Критическое значение F кр при заданных α, n 1 и n 2 определяется по таблице F- распределения Фишера или в Excel с помощью функции:
F кр = FРАСПОБР (α; n 1; n 2).
Из сравнения наблюдаемого значения F с критическим, получаем:
- если F < F кр, то Н 0 принимается, т.е. R 2 незначим;
- если F > F кр, то Н 0 отвергается, т.е. R 2 значим.
2. Наблюдаемому (расчетному) значению критерия F соответствует определенная значимость F, которую можно определить в Excel с помощью функции:
Значимость F = FРАСП (F; n 1; n 2).
Из сравнения значимости F с заданным стандартным уровнем значимости, получаем:
- если значимость F > стандартного уровня, то R 2 незначим;
- если значимость F <стандартного уровня, то R 2 значим.
Чаще всего F -тест используется для оценки того, значимо ли объяснение, даваемое уравнением в целом.