Оценку качества построенной модели дает коэффициент детерминации, а также средняя ошибка аппроксимации.
Средняя ошибка аппроксимации – среднее отклонение расчетных значений зависимой переменной от фактических:

Допустимый предел значений A – не более 8-10 %.
Пример 2.5. Построим регрессионные зависимости: а) расходов на питание (y) и личным доходом (x); б) расходов на питание (y) и временем (t) по следующим данным (усл. ед.):
| Год | |||||
| X | |||||
| Y |
и оценим качество подгонки.
а) Пусть истинная модель описывается выражением y = a + b x + e.
По выборочным наблюдениям определяем оценки (a; b).
Исходные данные и расчетные показатели представим в виде следующей расчетной таблицы:
| Год | X | Y | X 2 | Xy | 
| 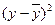
| 
| 
|
| -0,2 | 38,44 | 1,44 | ||||||
| 2,9 | 9,61 | 0,81 | ||||||
| 9,1 | 9,61 | 3,61 | ||||||
| 12,2 | 38,44 | 0,04 | ||||||
| Итого | 96,1 | 9,9 | ||||||
| Сред. | 84,8 | 21,2 | 19,22 | 1,98 | ||||
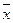
| 
| 
| 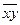
| 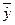
| 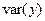
| 
| 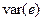
|
Окончательно имеем:
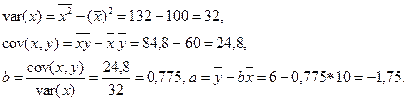
Cледовательно,  .
.
Коэффициент b = 0,775 показывает, что при увеличения дохода на 1 усл. ед расходы на питание увеличиваются в среднем на 0,775 усл. ед.
Замечание. В Excel оценки (a, b) можно также определить с помощью функций:
а = ОТРЕЗОК (массив y; массив x), b = НАКЛОН (массив y; массив x).
Условие  выполняется.
выполняется.
Качество подгонки оцениваем коэффициентом детерминации:
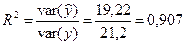 , т.е. 90,7 % вариации зависимой переменной (расходы на питание) объясняется регрессией.
, т.е. 90,7 % вариации зависимой переменной (расходы на питание) объясняется регрессией.
Значимость коэффициента R 2 проверяем по F -тесту
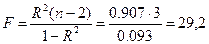 .
.
Произведем проверку значимости R 2 двумя способами.
1. При α = 0,05, n 1= 1 и n 2 = 3 по таблице или с помощью функции FРАСПОБР(α; n 1; n 2)[1] находим F кр = 10,13. Поскольку F = 29,2 > F кр = 10,13, то R 2 = 0,952 значим при 5 % уровне.
2. Наблюдаемому (расчетному) значению критерия F = 29,2 соответствует значимость F =0,0124, которую можно определить в Excel с помощью функции FРАСП(F; n 1; n 2)[2].
Поскольку значимость F = 0,0124 < 0,05, то R 2 значим при уровне 5 %.
б) Пусть истинная модель y = a + b t + e, (модель временного ряда). Выборочная регрессия 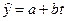 , где t – время, определяемое как t = 1 для 1990 г., t = 2 для 1991 г. и т.д.
, где t – время, определяемое как t = 1 для 1990 г., t = 2 для 1991 г. и т.д.
Представим исходные и расчетные показатели в виде расчетной таблицы:
| Год | t | Y | t 2 | ty | 
|
| –0,2 | |||||
| 2,9 | |||||
| 9,1 | |||||
| 12,2 | |||||
| Итого | |||||
| Среднее | 24,2 | ||||
| 
| 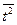
| 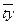
| 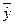
|
Окончательно имеем
 , следовательно,
, следовательно, 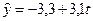 .
.
Коэффициент b = 3,1 показывает, что за год расходы на питание в среднем возрастают на 3,1 единиц.
Пример 2.6. Покажем, что в модели регрессии без свободного члена
Y = b X + e оценка МНК для b есть:
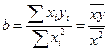 .
.
Выборочная регрессия для этой модели есть  . Наблюдаемые значения зависимой переменной связаны с расчетными уравнением
. Наблюдаемые значения зависимой переменной связаны с расчетными уравнением 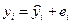 . Оценку b найдем из минимизации величины:
. Оценку b найдем из минимизации величины:
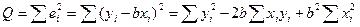 .
.
Запишем необходимые условия экстремума:
 , откуда
, откуда 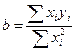 .
.
Вычисление R 2 при отсутствии свободного члена некорректно; при этом не выполняется условие  .
.
Пример 2.7. Покажем, что в модели регрессии Y = a + e оценка МНК для a есть:  .
.
Выборочная регрессия для заданной модели есть  . Наблюдаемые значения зависимой переменной связаны с расчетными значениями уравнением:
. Наблюдаемые значения зависимой переменной связаны с расчетными значениями уравнением: 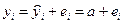 . Оценку a найдем из минимизации величины
. Оценку a найдем из минимизации величины
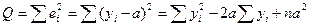 .
.
Запишем необходимые условия экстремума:
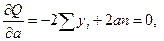 откуда
откуда 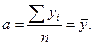
Выборочная регрессия 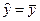 .
.
[1] F.ОБР.ПХ
[2] F.РАСП.ПХ