Приложение теории линейных пространств к решению систем линейных уравнений. Фундаментальная система решений

Рассмотрим систему линейных уравнений

Такая система называется неоднородной. Если b₁=b₂=…=b_s=0, тогда система линейных уравнений имеет вид

(1)

и называется однородной. Очевидно, что однородная система всегда совместна, то есть множество ее решений не пусто. В частности, решением любой однородной системы линейных уравнений будет решение: x₁=…=x_n=0. Это решение называется нулевым, или тривиальным.

Будем обозначать решение системы (1) вектором

x_a=(a₁, a₂, …, a_n),

то есть x_a будет решением системы (1), если

=0, i=1, 2, …, s.

Рассмотрим множество всех решений системы (1)

M={x_a½x_a=(a₁, a₂, …, a_n) Ù =0, i=1, 2, …, s}.

Теорема. М - линейное подпространство линейного пространства R⁽ⁿ⁾.

Доказательство

Очевидно, МÎ R⁽ⁿ⁾, поэтому можно воспользоваться теоремой о линейных подпространствах.

Пусть x_a_,x_bÎМ Ûx_a=(a₁,a₂,…,a_n) Ù =0, i=1,2,…,s Ù x_b=(b₁,b₂,…,b_n) Ù 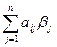=0, i=1,2,…,s Þ + = , " i=1,2,…,sÛ

Û x_a+x_bÎМ.

Пусть x_aÎМ Ûx_a=(a₁,a₂,…,a_n) Ù =0, i=1,2,…,sÞ"lÎR

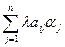l =0Û =0Û =0Ûlx_aÎМ. Оба условия теоремы о подпространстве выполнены, теорема доказана.

Размерность линейного пространства М не превосходит n и естественно встает вопрос о нахождении размерности линейного пространства М и его базиса.

Пусть ранг матрицы системы (1) равен r. Решим систему методом Гаусса.

(1)Û 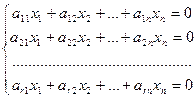(2)

(2) Û (3)

К системе (3) применяем правило Крамера. Это можно сделать, так как ранг матрицы системы равен r, следовательно, определитель системы (3) отличен от нуля.

x_j= , где D - определитель системы (3), а D⁽^j⁾(c) получен из определителя D заменой j-го столбца столбцом свободных членов и зависит от выбора с.

x₁= , x₂= 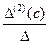,…, x_r= , x_r₊₁=c_r₊₁,…,x_n=c_n. (4)

При любом наборе значений произвольных постоянных c_r₊₁,…,c_n значения переменных x₁,x₂,…, x_r определяются однозначно. То есть, если рассматривать произвольный вектор x_aÎМ, то видим, что последние n-r координат выбираются произвольно, а первые r однозначно определены. Будем записывать решение системы в виде

x_a=(a₁⁰,a₂⁰,…,a_r⁰,a_r₊₁,…,a_n).

Теорема. Размерность пространства решений системы (1) линейных однородных уравнений с n неизвестными равна n-r, где r - ранг матрицы системы (1).

Доказательство

1. Если n=r, то, по теореме Кронекера - Капели, система имеет единственное решение (нулевое), и размерность пространства решений равна 0= n-r.

2. Пусть n>r. Рассмотрим пространство

R⁽ⁿ^-^r⁾={a½a=(a_r₊₁, a_r₊₂,…,a_n) }

Установим соответствие между векторами линейного пространства М и векторами арифметического пространства R⁽ⁿ^-^r⁾.

Пусть x_aÎМ Ûx_a=(a₁⁰,a₂⁰,…,a_r⁰,a_r₊₁,…,a_n), тогда ему соответствует вектор aÎ R⁽ⁿ^-^r⁾ такой, что a=(a_r₊₁, a_r₊₂,…,a_n).

Очевидно, что отображение R⁽ⁿ^-^r⁾ ® М, по закону j(a)=x_a, будет взаимнооднозначным.

Можно также показать, что это отображение сохраняет операции, действительно, если a,bÎ R⁽ⁿ^-^r⁾ Û

a=(a_r₊₁, a_r₊₂,…,a_n), b=(b_r₊₁, b_r₊₂,…, b_n), a+b=(a_r₊₁+b_r₊₁, a_r₊₂+b_r₊₂,…,a_n+b_n), тогда

j(a)=x_a=(a₁⁰,a₂⁰,…,a_r⁰,a_r₊₁,…,a_n), j(b)= x_b =(b₁⁰, b₂⁰,…, b_r⁰, b_r₊₁,…, b_n),

j(a+b)=x_g.

Для нахождения x_g мы должны в соотношения (3) вместо c_r₊₁,…,c_n подставить a_r₊₁+b_r₊₁, a_r₊₂+b_r₊₂,…,a_n+b_n и найти первые r неизвестных по формулам (4), где вместо всякого с подставляется сумма соответствующих a и b. То есть в каждом из определителей один столбец будет равен сумме двух слагаемых. Но тогда эти определители раскладываются на сумму двух определителей, например

x₁= = ,

таким образом,

j(a+b)=x_g= (a₁⁰+b₁⁰,a₂⁰+b₂⁰,…,a_r⁰+b_r⁰,a_r₊₁+b_r₊₁,…,a_n +b_n)= x_a +x_b =j(a)+j(b).

Мы доказали, что операция сложения сохраняется.

Самостоятельно показать, что сохраняется операция умножения вектора на действительное число.

Итак, R⁽ⁿ^-^r⁾ @ М, следовательно, они имеют одинаковые размерности, и образом базиса пространства R⁽ⁿ^-^r⁾ будет базис линейного пространства М. Но базис пространства R⁽ⁿ^-^r⁾ легко построить, в частности, базисом R⁽ⁿ^-^r⁾ будет система векторов:

e_r₊₁=(1,0,…,0)

e_r₊₂=(0,1,…,0)

……………….

e_n =(0,0,…,1)

Тогда базис линейного пространства М имеет вид

E₁=(l₁⁰, l₂⁰,.., l_r⁰,1,0,…,0)

E₂=(m₁⁰,m₂⁰,.., m_r⁰,0,1,…,0)

……………………………

E_n_-_r=(n₁⁰,n₂⁰,..,n _r⁰,0,0,…, 1)

Это один из базисов линейного пространства М, который называется нормальным базисом, тогда любой вектор линейного пространства М можно представить как линейную комбинацию векторов базиса, то есть

"x_aÎМ$ (x_a= k₁E₁+k₂E₂+…+k_n-rE_n-r).

Определение. Базис линейного пространства решений системы линейных однородных уравнений называется фундаментальной системой решений.

Можно определить фундаментальную систему решений системы линейных однородных уравнений как линейно независимую систему решений системы линейных однородных уравнений, через которую выражается любое решение системы линейных однородных уравнений.

Мы решали систему линейных однородных уравнений (1). Рассмотрим соответствующую систему линейных неоднородных уравнений

(5)

Общим решением системы линейных неоднородных уравнений (5) будем называть систему функций y₁=f₁(a_ij,b_i,c_i), y₂=f₂(a_ij,b_i_,c_i),…, y_n=f_n(a_ij,b_i,c_i), каждая из которых зависит от a_ij - коэффициентов системы линейных уравнений (5), b_i – свободных членов системы (5), c_i – произвольных параметров и обладает тем свойством, что подстановка этих функций вместо соответствующих неизвестных в (5) обращает каждое уравнение в тождество. И обратно, каждое решение системы (5) может быть получено при надлежащем выборе параметров c_i. Решение системы (5), которое получается из общего решения при фиксированных значениях параметров c_i, называется частным решением системы линейных уравнений (5).

Очевидно, приведенное определение справедливо и для системы (1) при b_i=0.

Теорема. Общее решение системы (5) представляет собой сумму общего решения системы (1) и частного решения системы (5).

Доказательство

Пусть Y=(y₁, y₂, …, y_n) - общее решение системы (5),

Y⁰=(y₁⁰, y₂⁰, …, y_n⁰) - частное решение системы (5), y_i ⁰=f_i(a_ij, b_i_,c_i),

X=(x₁, x₂, …, x_n) - общее решение системы (1), x_i=j_i(a_ij, 0,_,c_i).

Нужно доказать, что Y=X + Y⁰.

Покажем сначала, что Y - решение системы (5). Так как X - решение системы (1), то =0, а так как Y⁰- решение системы (5), тогда =b_i, i=1,2,…,s. Рассмотрим сумму j_j+y_j⁰=y_j. Очевидно, y_i=f_i(a_ij,b_i_,c_i). Подставим в систему (5), получим

0+ b_i= b_i, i=1,2,…,s.

Таким образом, y_j обращает каждое уравнение в тождество, то есть система функций y_j- решение системы (5). С другой стороны, если y₁=f₁(a_ij,b_i,c_i), y₂=f₂(a_ij,b_i_,c_i),…, y_n=f_n(a_ij,b_i,c_i) есть общее решение системы (5), то есть

= b_i, (*)

Если Y⁰- частное решение системы (5), тогда

=b_i. (**)

Рассмотрим разность Y-Y⁰= X. Из соотношений (*) и (**) получим

то есть Х будет решением системы (1), и, следовательно, все решения системы (5) содержатся в функциях вида Y= X + Y⁰.

Определение. Рассмотрим линейное пространство V. Пусть aÎV – произвольный, но постоянный вектор. Отображение t пространства V в себя такое, что образом всякого вектора х служит вектор t(х)=х+а, называется переносом пространства V на вектор а.

Определение. Рассмотрим L – линейное подпространство линейного пространства V, перенос линейного подпространства на вектор а называется линейным многообразием линейного пространства V.

Вообще говоря, а не обязательно принадлежит L. В общем случае линейное многообразие не является линейным подпространством. За размерность линейного многообразия принимают размерность того подпространства, сдвигом которого оно было получено. Если вернуться к только что доказанной теореме, имеем Х есть линейное подпространство R⁽ⁿ⁾, Y⁰- фиксированный вектор в пространстве R⁽ⁿ⁾, тогда можно считать Y линейным многообразием линейного пространства R⁽ⁿ⁾, заданным системой линейных уравнений.

Примеры

1. Решить систему линейных однородных уравнений

(6)

Будем решать систему методом Гаусса. Выпишем расширенную матрицу системы и упростим ее.

~ ~ ~

Получили систему, равносильную данной

Û .

Система линейных уравнений имеет бесчисленное множество решений. Общее решение имеет вид (0,2с; -1,4с; с; 0). Фундаментальная система решений состоит из одного вектора Е=(0,2; -1,4; 1; 0). Все решения системы линейных уравнений (6) можно записать следующим образом х=lЕ.

2. Решить систему линейных однородных уравнений