Пусть L1 и L2 - линейные подпространства линейного пространства V. По аналогии с теорией множеств можно рассмотреть операции над линейными подпространствами.
1. Пересечением линейных подпространств L1 и L2 называется множество
L0={x½xÎ L1ÙxÎL2}=L1ÇL2.
Используя теорему о подпространстве, легко показать, что пересечение двух линейных подпространств линейного пространства V само является линейным подпространством линейного пространства V. Действительно, пусть
x,yÎ L0Û xÎL1ÙxÎL2Ù yÎL1Ù y ÎL2Ûx+yÎL1Ùx+ yÎL2Û x+ yÎL0.
Аналогично,
пусть xÎ L0 и lÎR Û xÎ L1ÙxÎL2ÙlÎRÛ lxÎ L1ÙlxÎL2 ÛlxÎ L0.
Оба условия теоремы выполнены, следовательно, L0 - линейное подпространство линейного пространства V.
2. суммой линейных подпространств L1 и L2 линейного пространства V называется множество
 =L1+L2 ={x½x=x1+x2 Ùx1Î L1Ùx2ÎL2}.
=L1+L2 ={x½x=x1+x2 Ùx1Î L1Ùx2ÎL2}.
Если представление элементов множества  как суммы элементов множеств L1 и L2 является однозначным, то сумма называется прямой и обозначается
как суммы элементов множеств L1 и L2 является однозначным, то сумма называется прямой и обозначается 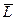 = L1ÅL2.
= L1ÅL2.
Так как L1ÌV и L2ÌV, то, очевидно,  ÌV. Покажем, что
ÌV. Покажем, что  - линейное подпространство линейного пространства V. Действительно, пусть
- линейное подпространство линейного пространства V. Действительно, пусть
x,yÎ 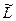 Û x=x1+x2 Ùx1Î L1Ùx2ÎL2Ù y=y1+y2 Ùy1Î L1Ùy2ÎL2Û
Û x=x1+x2 Ùx1Î L1Ùx2ÎL2Ù y=y1+y2 Ùy1Î L1Ùy2ÎL2Û
x+y=(x1+x2)+(y1+y2)=(x1+y1)+(x2+y2) Î 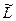 , так как x1+y1Î L1Ù x2+y2ÎL2.
, так как x1+y1Î L1Ù x2+y2ÎL2.
Аналогично, пусть xÎ 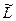 Û x=x1+x2 Ùx1Î L1Ùx2ÎL2 и пусть lÎR, тогда
Û x=x1+x2 Ùx1Î L1Ùx2ÎL2 и пусть lÎR, тогда
lx1Î L1Ùlx2ÎL2Ûl x=l(x1+x2)= lx1+lx2Î 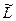 .
.
Оба условия теоремы выполнены, следовательно, 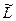 - линейное подпространство линейного пространства V.
- линейное подпространство линейного пространства V.
Примеры
Пусть V – обычное трехмерное геометрическое пространство. L1 - множество векторов, лежащих в плоскости a, L2 - множество векторов, лежащих в плоскости b, причем a^b, тогда L1+L2 совпадает с пространством V, причем эта сумма не будет прямой, что хорошо видно на примере.
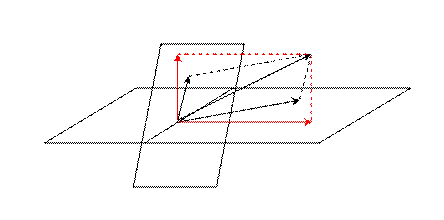
a
b
Теорема. Размерность суммы линейных подпространств равна сумме их размерностей минус размерность пересечения, то есть
dim 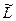 =dim(L1+ L2)=dimL1+dimL2-dim L1Ç L2
=dim(L1+ L2)=dimL1+dimL2-dim L1Ç L2
Доказательство
Пусть L1 и L2 – линейные подпространства линейного пространства V, обозначим dimL1=m1, dimL2=m2, L0=L1ÇL2, dimL0=m0, 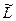 =L1+ L2, dim
=L1+ L2, dim 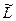 =
=  и докажем, что
и докажем, что  = m1+ m2- m0.
= m1+ m2- m0.
Рассмотрим базис пространства L0 , он состоит из m0 векторов:
e1,e2,…,  (1)
(1)
Так как e1,e2,…,  Î L0, то e1,e2,…,
Î L0, то e1,e2,…,  ÎL1 и e1,e2,…,
ÎL1 и e1,e2,…,  ÎL2.Дополним систему векторов (1) до базиса пространства L1:
ÎL2.Дополним систему векторов (1) до базиса пространства L1:
e1,e2,…, 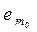 ,
, 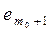 …
…  (2)
(2)
и до базиса пространства L2:
e1,e2,…,  ,
,  …
…  (3)
(3)
По определению базиса,
"aÎL1$a1,a2,…, 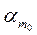 ,
, 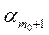 ,…,
,…, 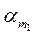 ÎR(a=a1e1+…+
ÎR(a=a1e1+…+ 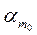
 +…+
+…+ 
 ).
).
Аналогично
"bÎL1$b1,b2,…, 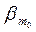 ,
, 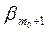 ,…,
,…,  ÎR(b=b1e1+…+
ÎR(b=b1e1+…+ 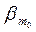
 +…+
+…+ 
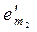 ).
).
Теперь рассмотрим линейное пространство
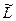 =L1+L2 ={x½x=x1+x2 Ùx1Î L1Ùx2ÎL2},
=L1+L2 ={x½x=x1+x2 Ùx1Î L1Ùx2ÎL2},
тогда " xÎ 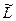 имеем x=a+b = =(a1e1+…+
имеем x=a+b = =(a1e1+…+ 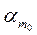
 +…+
+…+ 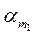
 )+(b1e1+…+
)+(b1e1+…+ 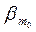
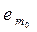 +…+
+…+ 
 ) =
) =
=(a1+b1)e1+…+(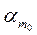 +
+  )
) 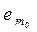 +
+ 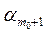
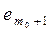 +
+ 
 +… +
+… + 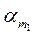
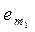 + +
+ + 
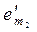 (4)
(4)
Из полученного соотношения (4) следует, что произвольный вектор линейного пространства 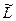 является линейной комбинацией векторов
является линейной комбинацией векторов
e1,e2,…,  ,
, 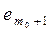 …
…  ,
,  …
…  (5)
(5)
то есть линейное пространство 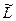 является линейной оболочкой системы векторов (5). Покажем, что эта система векторов линейно независима.
является линейной оболочкой системы векторов (5). Покажем, что эта система векторов линейно независима.
Предположим противное. Пусть существуют такие действительные числа
l1, l2,…,  ,
, 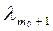 ,…,
,…,  ,
, 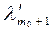 ,…,
,…, 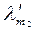 , что
, что
l1 e1 +…+ 
 +
+ 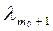
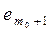 +…+
+…+ 
 +
+ 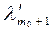
 +…+
+…+ 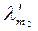
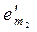 =0 (*)
=0 (*)
и среди коэффициентов есть отличные от нуля.
Преобразуем последнее равенство
l1 e1 +…+ 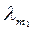
 =-(
=-(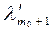
 +…+
+…+ 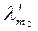
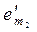 )=с, где сÎ L1, так как с=l1 e1 +…+
)=с, где сÎ L1, так как с=l1 e1 +…+ 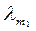
 является линейной комбинацией векторов базиса (2). Кроме того, сÎ L2, так как с=-(
является линейной комбинацией векторов базиса (2). Кроме того, сÎ L2, так как с=-(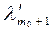
 +…+
+…+ 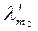
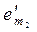 ) – линейная комбинация векторов линейного пространства L2. Следовательно,
) – линейная комбинация векторов линейного пространства L2. Следовательно,
сÎ L0=L1ÇL2, но тогда вектор с можно разложить по базису (1)
с=m1e1+m2e2+…+ 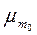
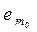 =-(
=-(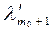
 +…+
+…+ 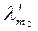
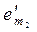 ).
).
Отсюда следует
m1e1+m2e2+…+ 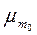
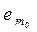 +
+ 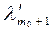
 +…+
+…+ 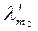
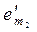 =0,
=0,
так как это - линейная комбинация векторов базиса (3), то равенство нулю означает, что равны нулю все коэффициенты, то есть
m1=m2=…= 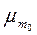 =
= 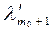 =…=
=…= 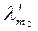 =0 Û с=0Ûl1 e1 +…+
=0 Û с=0Ûl1 e1 +…+ 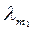
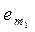 =0, а это линейная комбинация векторов базиса (2), и, следовательно, равенство нулю означает, что равны нулю все коэффициенты, то есть l1=…=
=0, а это линейная комбинация векторов базиса (2), и, следовательно, равенство нулю означает, что равны нулю все коэффициенты, то есть l1=…= 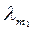 =0. Таким образом, мы получили, что равенство (*) возможно только в том случае, когда все коэффициенты равны нулю, а это, в свою очередь, означает, что система векторов (5) линейно независима. Поэтому система векторов (5) является базисом линейной оболочки
=0. Таким образом, мы получили, что равенство (*) возможно только в том случае, когда все коэффициенты равны нулю, а это, в свою очередь, означает, что система векторов (5) линейно независима. Поэтому система векторов (5) является базисом линейной оболочки 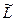 , порожденной этими векторами. Число векторов в базисе (5) равно размерности линейного пространства
, порожденной этими векторами. Число векторов в базисе (5) равно размерности линейного пространства 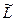 и равно
и равно 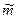 = m1+ m2- m0, что и требовалось доказать.
= m1+ m2- m0, что и требовалось доказать.
Следствие. Размерность прямой суммы линейных подпространств равна сумме их размерностей.
Доказательство
Для доказательства достаточно показать, что 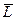 = L1ÅL2.Þ L1ÇL2 ={0}.
= L1ÅL2.Þ L1ÇL2 ={0}.
Действительно, если предположить противное, то есть найдется ненулевой вектор сÎL1ÇL2, тогда сÎL1 и сÎL2 , следовательно, 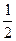 сÎL1 и
сÎL1 и 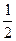 сÎ L2,
сÎ L2, 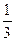 сÎL1 и
сÎL1 и 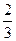 сÎ L2, тогда с=
сÎ L2, тогда с= 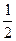 с+
с+ 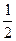 с=
с= 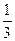 с+
с+  с. Получили противоречие, L1ÇL2 ={0} и следствие доказано.
с. Получили противоречие, L1ÇL2 ={0} и следствие доказано.
Евклидовы пространства
Пусть V=(V,+,W) – линейное пространство над полем R. Будем говорить, что в линейном пространстве V задано скалярное умножение, если задано отображение V´V®R, удовлетворяющее следующим аксиомам:
1° "a,bÎV ((a,b)=(b,a))
2° "a,b,cÎV ((a+c,b)=(a,b)+(c,b))
3° "a,bÎV"lÎ R ((la,b)= l(a,b))
4° "aÎV (a¹0Þ(a,a)>0)
Следствие из аксиом. Если a=0 или b=0, тогда (a,b)=0.
Примеры
1. Рассмотрим линейное пространство векторов на плоскости, а скалярное произведение определим так:
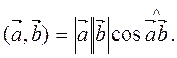
Самостоятельно показать, что все аксиомы выполняются.
2. Если рассмотреть множество функций, непрерывных на сегменте [a,b], ввести операции сложения и умножения на действительное число, получим линейное пространство. Скалярное произведение в этом пространстве можно ввести следующим образом:
(f (x) ,g (x))= 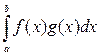 .
.
Самостоятельно показать, что все аксиомы выполняются.
Определение. Линейное пространство, в котором введено скалярное умножение, называется Евклидовым пространством.
В любом n-мерном линейном пространстве можно ввести скалярное умножение векторов. Действительно, пусть V – n-мерное линейное пространство и e1,e2,…,en – базис этого пространства, тогда любой вектор линейного пространства V можно представить как линейную комбинацию векторов базиса, то есть "a,bÎV(а=  , b=
, b= 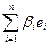 ). Введем операцию умножения векторов по правилу
). Введем операцию умножения векторов по правилу
(a,b)= 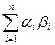 ÎR.
ÎR.
Проверим, будет ли данное умножение скалярным произведением, для этого проверим все аксиомы
1° "a,bÎV ((a,b)= 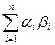 =
= 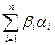 =(b,a))
=(b,a))
2° "a,b,cÎV ((a+c,b)=  = (a,b)+(c,b))
= (a,b)+(c,b))
3° "a,bÎV"lÎ R ((la,b)= 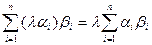 = l(a,b))
= l(a,b))
4° "aÎV (a¹0Þ(a,a)=  >0)
>0)
Все аксиомы выполнены, следовательно, мы получили евклидово пространство. Это говорит о том, что любое конечномерное линейное пространство можно преобразовать в евклидово. Далее будем рассматривать евклидовы пространства и обозначать их Е(n).
Определение. Назовем длиной вектора а величину, равную арифметическому квадратному корню из скалярного квадрата
ô а ô= 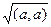 .
.
Определение. Назовем углом между векторами a¹0 и b¹0 угол
j=arccos 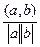 , 0£j£p.
, 0£j£p.
Докажем корректность этого определения, то есть нужно показать, что
-1£ 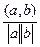 £1Û
£1Û 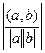 £1Û
£1Û  £1.
£1.
Рассмотрим скалярный квадрат вектора a-lb, где lÎ R, имеем
(a-lb, a-lb)=(a, a-lb)+(-lb, a-lb)=(a,a) +(a,-lb)+(-lb, a)+(-lb,-lb)=
=(a,a)-l(a,b)- -l(b,a)+ l2(b,b)= l2(b,b)-2l(a,b)+(a,a)³0 "lÎR.
Если рассмотреть последнее соотношение как квадратное неравенство относительно переменной l, тогда имеем (b,b)>0, и неравенство верно "lÎR, следовательно,
D=(a,b)2-(a,a)(b,b) £0Û (a,b)2£(a,a)(b,b) Û  £1, что и требовалось доказать.
£1, что и требовалось доказать.
Из неравенства (a,b)2-(a,a)(b,b) £0 можно получить интересное следствие.
Пусть дано пространство, и скалярное произведение в нем определено следующим образом (a,b)=  , тогда получим
, тогда получим
(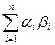 )2-
)2- 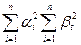 £0Û(a1b1+a2b2+…+anbn)2£(a12+…+ an2)(b12+…+ bn2).
£0Û(a1b1+a2b2+…+anbn)2£(a12+…+ an2)(b12+…+ bn2).
Это неравенство Коши – Буняковского.
Определение. Два вектора a¹0 и b¹0 называются ортогональными, если угол между ними равен 90° или (a,b)=0.
Определение. Система векторов
a1,a2,…,as (1)
называется ортогональной, если любая пара векторов этой системы ортогональна, то есть
"i¹j ((ai,aj)=0).
Теорема. Ортогональная система векторов линейно независима.
Доказательство
Пусть система векторов (1) – ортогональная. Рассмотрим их линейную комбинацию
a1a1+a2a2+…+asas=0 (2)
и покажем, что равенство 0 обязательно влечет за собой равенство нулю всех коэффициентов. Умножим обе части равенства (2) скалярно на a1, получим
(a1a1+a2a2+…+asas,a1)=(0,a1) Û (a1a1,a1)+(a2a2,a1)+…+(a sas ,a1)=0 Û
Ûa1(a1,a1)+ a2(a2,a1)+…+ a s(as ,a1)=0,
но (ai,aj)=0, если i¹j, то есть (a2,a1)=…=(as ,a1)=0. Следовательно, получаем
a1(a1,a1)=0 и (a1,a1)>0, отсюда a1=0. Аналогично, умножая равенство (2) скалярно на a2,…,as, получим a2=…=as=0, что и требовалось доказать, следовательно, система векторов (1) линейно независима.
Из доказанной теоремы следует, что всякая ортогональная система векторов евклидова пространства линейно независима. Возникает вопрос о переходе от линейно независимой системы векторов к ортогональной, содержащей такое же количество векторов. Такой процесс называется процессом ортогонализации. Дадим индуктивное определение процесса ортогонализации:
1. Пусть система векторов a1, a2 (s=2) линейно независима (очевидно, a1¹0,a2¹0). Рассмотрим новую систему векторов b1=a1, b2=aa1+a2, где a - неизвестный числовой параметр, который найдем из условия (b1,b2)=0:
(b1,b2)=(a1,aa1+a2)=a(a1,a1)+(a1,a2)=0 Þ a=-  .
.
Таким образом, мы построили ортогональную систему из двух векторов.
2. Пусть имеем линейно независимую систему векторов
a1,a2,…,as (1)
Предположим, что для любого k (2£k<s) ортогональная система векторов построена
b1,b2,…,bk.
Добавим еще один вектор bk+1=a1b1+a2b2+…+akbk+ ak+1.
Самостоятельно показать, что bk+1¹0.
Коэффициенты ai будем вычислять из условия, что
(bk+1,bi)=0Û(a1b1+a2b2+…+akbk+ ak+1,bi)=0Û
a1(b1,bi)+ …+ai(bi,bi)+…+ ak(bk,bi)+(ak+1,bi)=0Ûai(bi,bi)+(ak+1,bi)=0Þ
ai=- 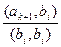 .
.
получим ортогональную систему векторов b1,b2,…,bk bk+1.
Следствие. Пусть a1,a2,…,anÎЕ(n) и являются базисом Е(n). Так как базис - это линейно независимая система, то его можно ортогонализировать. Очевидно, полученная ортогональная система векторов также будет базисом пространства Е(n). То есть в любом евклидовом пространстве существует ортогональный базис.
Пусть а¹0ÎЕ(n). Рассмотрим вектор е= 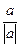 . Очевидно, ôеô=1. Операция перехода от вектора а к вектору е называется нормированием, а полученный вектор – нормированным или нормальным. Любой ненулевой вектор можно аналогичным образом пронормировать. Если пронормировать векторы ортогонального базиса, то получим ортонормированный базис евклидова пространства e1,e2,…,en,где ôеiô=1"i=1,…,n, (ei,ej)=
. Очевидно, ôеô=1. Операция перехода от вектора а к вектору е называется нормированием, а полученный вектор – нормированным или нормальным. Любой ненулевой вектор можно аналогичным образом пронормировать. Если пронормировать векторы ортогонального базиса, то получим ортонормированный базис евклидова пространства e1,e2,…,en,где ôеiô=1"i=1,…,n, (ei,ej)= 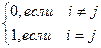 .
.
Скалярное произведение любых векторов евклидова пространства тогда и только тогда равно сумме произведений одноименных координат, когда эти векторы заданы в ортонормированном базисе.