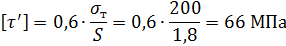Корпус механизма представляет собой консольную стойку. Примем сечение стойки в виде тавра. Осевая сила Q винта действует на расстоянии L от главной центральной оси ZC сечения стойки.
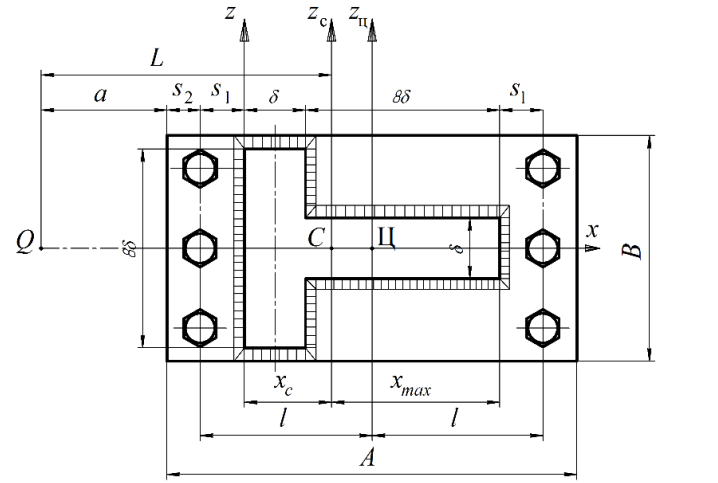
Рис. 9. Тавровое сечение стойки, сварной шов и расположение болтов
Примем размер тавра 9δ х 8δ. Диаметр болтов примем в первом приближении s1 = s2 = 15 мм.Стойка в опасном сечении работает на растяжение от силы Qи изгиб от момента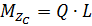 
Толщина стенки тавра определяется по формуле
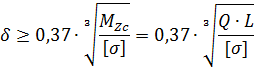
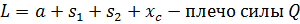
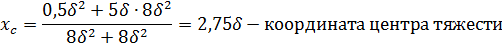
Отсюда получаем для определения требуемого значения толщины стенки тавра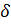 
кубическое уравнение в виде
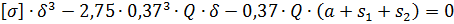
Решение уравнения дано в виде графиков на рис. 10.
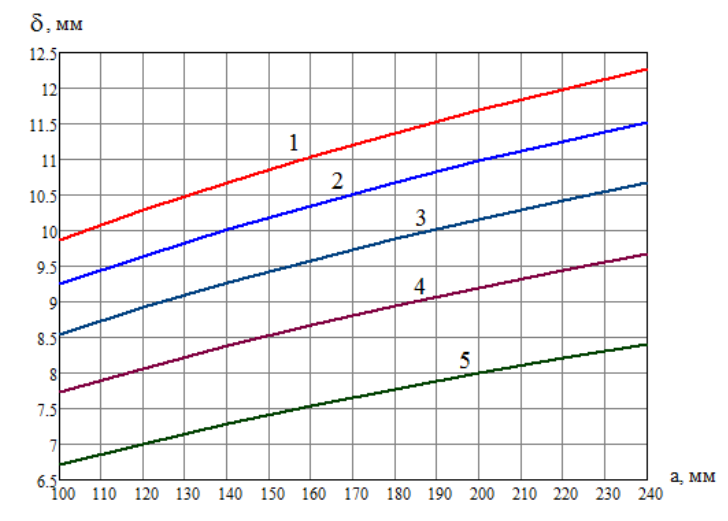
Рис.10. Зависимость толщины стенки от нагрузки Q и расстояния а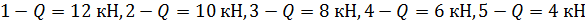 
Из рис.10. следует, что при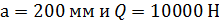 
требуемая толщина стенки тавра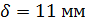 
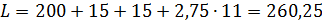
Момент инерции относительно оси Zc
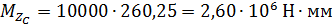
Момент инерции сечения тавра относительно главной центральной оси по формуле
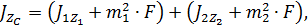
где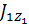 
и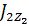 
– моменты инерции фигур 1 и 2 относительно собственных осей, определяемые по формулам
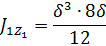
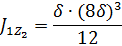
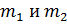- расстояния от главной центральной оси Zcдо собственных осей Z1 и Z2 фигур 1 и 2
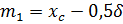
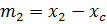
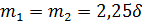
После подстановки входящих величин получим формулу главного момента инерции тавра
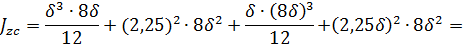
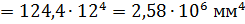
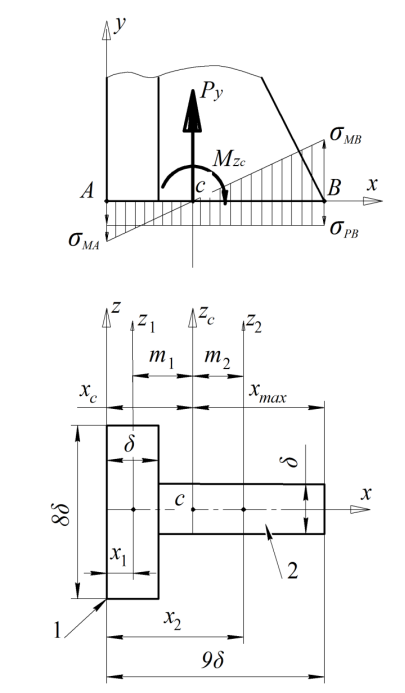
Рис.11. Схема к расчету корпуса механизма
Координата центра тяжести тавра в исходной системе координат xz
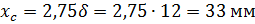
Изгибающие напряжения в основании стойки в точках B
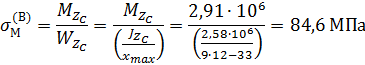
Изгибающие напряжения по рис.11. в точках A
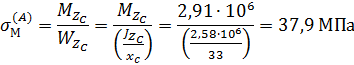
Напряжения растяжения от силы Q в основании стойки
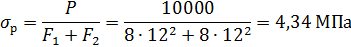
Суммарные напряжения в опасных точках A и B сечения тавра
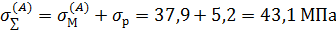
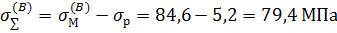
Напряжения не превышают допускаемое, принятое равным 100 МПа. Условия прочности выполняются, прочность стойки рассчитанного сечения обеспечена.
5. Расчет сварных соединений корпуса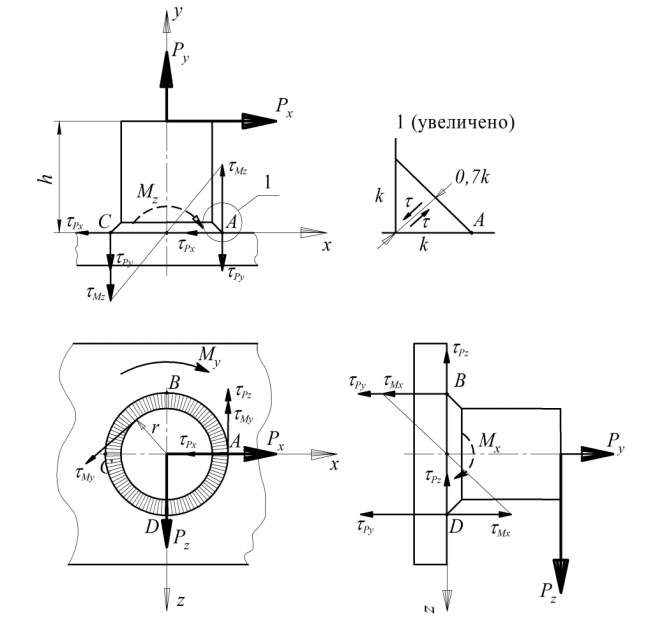 
Рис. 12. Расчетная схема сварного таврового соединения
Примем в первом приближении катет углового шва k = 12 мм. Расчет ведётся по касательным напряжениям в сечении 0,7 k. Из расчетной схемы на рис. 41следует, что сила Q создает в шве напряжения τQ, а момент MZc создает напряжения τм. Картина напряжений при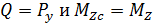 
дана на рис. 12. на примере кольцевого шва. В нашем примере (см. рис. 9) таврового сечения стойки площадь шва по контуру тавра (рис. 13)
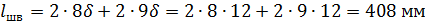
Напряжения от силы Q
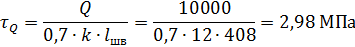
Момент инерции контура шва вокруг тавра относительно главной центральной оси (см. рис. 13) равен сумме моментов инерции отдельных контуров шва относительно этой оси. Общий контур состоит из швов: 1, 2, 3, 4, 5. При этом, имеем два шва №2, два шва №3 и два шва №4. Каждый шов имеет свой центр тяжести в системе координат XZ. Положение центров тяжести всех пяти швов определяется по рис. 13 в исходной системе координат XZ
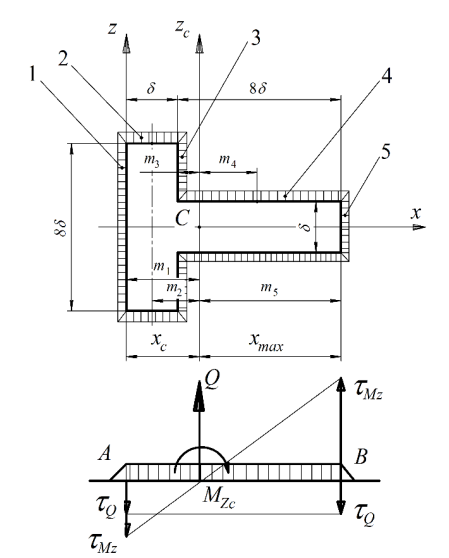
Рис. 13. Контур сварного шва тавра
Момент инерции шва №1 относительно оси ZC , проходящей через общий центр тяжести швов в точке C (см. рис. 41):
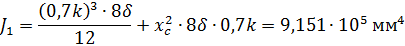
Момент инерции двух швов №2:
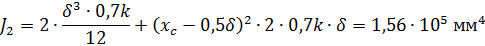
Момент инерции двух швов №3
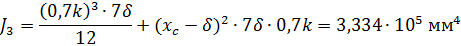
Момент инерции двух швов №4
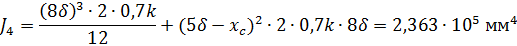
Момент инерции шва №5
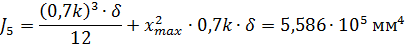
Суммарный момент инерции шва относительно главной центральной оси шва
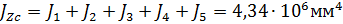
Напряжения в точке А шва (см. рис. 35 и 41) от действия момента MZc
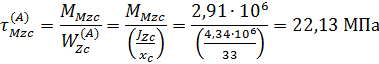
Суммарное напряжение в точке А шва по эпюре на рис. 13
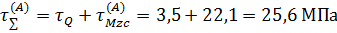
Напряжения в точке B шва по эпюре на рис. 13
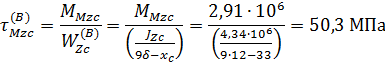
Суммарное напряжение в точке В шва по эпюре на рис. 13
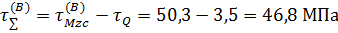
Условие прочности в опасных точках шва выполняется:
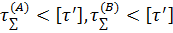
Допускаемые напряжения сварного шва для материала сталь Ст.3
