ЭЛЕКТРОДИНАМИЧЕСКИЕ СИЛЫ, ЗАДАЮЩИЕ РАССТОЯНИЯ МЕЖДУ АТОМНЫМИ СЛОЯМИ В ГРАФИТЕ
А.А.Гришаев, независимый исследователь
Введение.
Углерод, как известно, легко образует плёнки толщиной в один атомный слой. В частности, идеальная структура графита образована из таких плёнок – из параллельных атомных слоёв, в которых атомы углерода расположены в вершинах примыкающих друг к другу правильных гексагонов. Расстояния между атомами в этих гексагонах есть 1.42 Å, расстояние же между атомными плоскостями гораздо больше: 3.4 Å [1]. Каков физический механизм, определяющий равновесные расстояния между атомными слоями в графите? В рамках традиционных представлений, наиболее известны два подхода. Согласно первому [1,2], все четыре валентных электрона у каждого атома углерода образуют четыре связи в пределах атомной плоскости – так, что каждый углеродный гексагон имеет тройку одинарных и тройку двойных связей – а расстояния между плоскостями определяются ван-дер-ваальсовыми силами. Однако, ван-дер-ваальсовы силы играют заметную роль при достаточно близком соседстве полярных молекул, когда их притяжение обусловлено притяжением их электрических диполей, а отталкивание обусловлено силами, возникающими, якобы, при контакте молекул и соприкосновении их электронных орбиталей. Тогда равновесное расстояние между молекулами должно почти совпадать с расстоянием, на котором они соприкасаются – что совершенно не подходит к случаю огромных, по атомным меркам, расстояний между атомными плоскостями в графите. Согласно второму подходу (см., например, [3]), в углеродной атомной плоскости задействованы по три валентных электрона на атом, так что все связи в углеродных гексагонах являются одинарными. Свободные же валентности, которых остаётся по одной на атом, направлены ортогонально атомной плоскости, и при этом они чередуются так, что у одной тройки атомов гексагона они находятся по одну сторону плоскости, а у другой тройки – по другую. Полагают, что встречные свободные валентности двух углеродных атомных слоёв могут образовывать слабые химические связи (p-связи) – чем, якобы, и определяется расстояние между этими слоями. Однако, если из этого расстояния, 3.4 Å, вычесть удвоенный экспериментальный радиус атома углерода, около 0.7 Å [4], то получается свободный зазор в 2 Å. Мы не нашли объяснений того, каким это чудесным образом у атомов углерода образуются p-орбитали, которые длиннее экспериментального атомного радиуса, как минимум, в 2.5 раза – ради того, чтобы образовать слабые связи между атомными слоями.
Загадку равновесного расстояния между атомными плоскостями в графите мы попытаемся разрешить с использованием второй из названных моделей, согласно которой, атомная плоскость в графите является, фактически, трёхслойной – плоский атомный каркас находится между двумя слоями валентных электронов. Но мы дополним эту модель нашими представлениями о валентных электронах [5]. Согласно этим представлениям, эффективный электрический заряд у валентной связки «протон-электрон» не является постоянным во времени и равным нулю – он испытывает колебания с размахом от - e до + e (e – элементарный электрический заряд) и на частотах, распределение которых при тепловом равновесии соответствует равновесному спектру. В результате, в углеродном атомном слое распределение электрических зарядов не является статическим: происходят колебания эффективного заряда в самом атомном каркасе и в ортогональных ему свободных валентных связках. Мы постараемся показать, что электродинамическое взаимодействие двух таких атомных слоёв даёт, при определённых условиях, устойчивое равновесное расстояние между ними – близкое к тому, которое и характерно для графита. Кроме того, наш подход позволит качественно объяснить некоторые удивительные свойства углеродных каркасов – однослойных и многослойных.
Подводящий пример: взаимодействие двух соосных валентных связок.
В качестве подводящего примера рассмотрим взаимодействие двух соосных валентных связок «протон-электрон», как схематически изображено на Рис.1, где Q1 и Q4 обозначают
Рис.1
положительные заряды протонов, а Q2 и Q3 – отрицательные заряды электронов. Пусть D - расстояние между протонами, а s - длины валентных связок. Теорема Ирншоу гласит, что не может быть устойчива статическая конфигурация системы точечных зарядов. При этом подразумевается, что каждый заряд постоянен во времени. Но, как мы увидим ниже, если эффективные величины зарядов периодически изменяются, то статическая конфигурация системы таких зарядов может быть устойчива.
Следует уточнить, что, говоря про изменяемость зарядов, мы отнюдь не допускаем наличия у частиц дробных значений элементарного заряда e. На наш взгляд, частица либо имеет электрический заряд, т.е. квантовые пульсации на электронной частоте [6], либо – не имеет. Но эффективные величины зарядов в валентной связке «протон-электрон» могут изменяться. Как мы излагали ранее [5], алгоритм, формирующий атомарную связку «протон-электрон», попеременно прерывает квантовые пульсации на электронной частоте у этих протона и электрона – т.е., попеременно отправляет их электрические заряды в небытие. Для валентных связок «протон-электрон» допускается уход скважности этих попеременных прерываний в обе стороны от центрального значения 50% - в результате чего будет доминировать во времени либо элементарный заряд протона, либо элементарный заряд электрона.
При наличии у валентной связки «протон-электрон» энергии возбуждения, скважность попеременных прерываний гармонически изменяется с размахом от 0% до 100% [7], т.е. эффективный заряд этой пары изменяется с размахом от - e до + e. Частота же этих колебаний эффективного заряда равна частоте кванта энергии возбуждения. При этом, изменение во времени эффективных зарядов протона и электрона в валентной связке иллюстрирует Рис.2,

Рис.2
где показан только один период колебаний. Для эффективных зарядов валентных связок на Рис.1 можно записать:
Q1=(e /2)(1+Sin wt);
Q2=(e /2)(-1+Sin wt);
Q3=(e /2)(1+Sin(wt +j));
Q4=(e /2)(-1+Sin(wt +j)), (1)
где w - круговая частота, соответствующая энергии возбуждения, j - фазовый сдвиг между колебаниями эффективных зарядов в той и другой связках. Силы кулоновских взаимодействий между зарядами из разных связок есть
F 13~Q1Q3/(D - s)2;
F 14~Q1Q4/ D 2;
F 23~Q2Q3/(D -2 s)2;
F 24~Q2Q4/(D - s)2. (2)
Усреднённая во времени сила, действующая между нашими валентными связками, есть
 , (3)
, (3)
где T - интервал усреднения. Положительность этой силы означает отталкивание наших валентных связок, а отрицательность – их притяжение. Зависимость F (D) приведена, в относительных единицах, на Рис.3 для случая j=p. Машинные расчёты проводились для
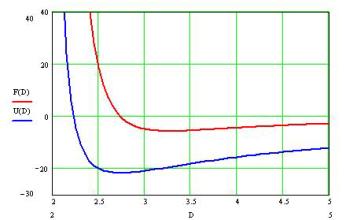
Рис.3
длин валентных связок s, равных единице, поэтому значения D на оси абсцисс Рис.3 выражают отношения D / s. В дополнение к зависимости усреднённой силы F (D), на Рис.3 приведена соответствующая зависимость «эффективной потенциальной энергии» U (D), рассчитанная способом, аналогичным вышеизложенному – с той разницей, что в знаменателях выражений, аналогичных (2), ставятся не квадраты расстояний, а их первые степени.
Как можно видеть, равновесное расстояние между протонами, соответствующее переходу через ноль кривой F (D) и минимуму «потенциальной ямы» U (D), составляет около 2.74, что в 1.37 раз превышает сумму длин валентных связок. Это их равновесное расположение на небольшом расстоянии друг от друга обладает некоторым запасом устойчивости по фазовому сдвигу: при уходе j от значения p, равновесное значение D увеличивается, но крутизна стенок и глубина «потенциальной ямы» уменьшаются – вплоть до её вырождения и пропадания устойчивого равновесия. Этого следовало ожидать, поскольку при j=0 синхронность изменений одноимённых эффективных зарядов электронов – самой близкой пары – должна давать доминирование сил отталкивания при любом расстоянии D.