Практическое занятие № 1.
Тема: Плоская система сходящихся сил.
Знать: геометрический и аналитические способы определения равнодействующей системы сил, условия равновесия плоской системы сходящихся сил.
Уметь: определять равнодействующую, решать задачи на равновесие.
Цель: Определение равновесия сходящейся системы сил геометрическим и аналитическим способом.
Задачи:1.О пределить равнодействующую сходящейся системы сил аналитическим и геометрическим способами.2.Определить находится ли данная система сил в равновесии геометрическим и аналитическим способом. 3. Рассчитать погрешность вычисления.
Практическая часть:
Задание 1. Определение равнодействующей системы сходящихся сил геометрическим способом.
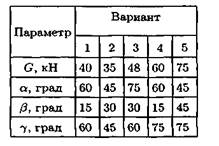
| Дано: сх сс | Вариант | ||||
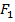 ,кН ,кН
| |||||
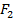 ,кН ,кН
| |||||
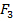 ,кН ,кН
| |||||
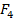 ,кН ,кН
| |||||
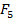 ,кН ,кН
| |||||
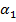 , град , град
| |||||
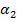 , град , град
| |||||
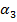 , град , град
| |||||
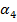 , град , град
| |||||
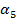 , град , град
|
Рекомендации для определения равнодействующейсистемы сходящихся сил геометрическим способом.
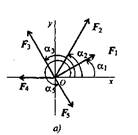
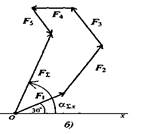
1. Данные векторов сил (таблица) изобразить графически в осях ОХ, ОУ, исходящими из точки начала координат О (рис а) в определенном масштабе.
2. Вычертите многоугольник заданной системы сил (рис б):
- Вычерчивайте в некотором масштабе силы системы один за другим в любой последовательности, чтобы конец предыдущего вектора совпадал с началом последующего.
- Соедините начало первого вектора с концом и концом последнего и направить ему навстречу – получите вектор равнодействующей силы (подпишите его 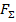 ).
).
3. Измерьте полученный вектор равнодействующей силы линейкой. Определите модуль равнодействующей силы в соответствии с выбранным масштабом и запишите его цифрой, проставив единицы измерения.
4. Измерьте угол наклона равнодействующей силы к оси ОХ транспортиром и запишите его.
5. Определите геометрическим способом – находится ли данная система сил в равновесии:
Если плоская система сходящихся сил находится в равновесии, многоугольник сил должен быть замкнут.
Рекомендации для определения равнодействующую системы сходящихся сил аналитическим способом.
Расчетная таблица
Графическое изображение F, 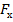 , , 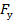 в координатах ОХ, ОУ в координатах ОХ, ОУ
| Расчет проекции 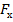
| Расчет проекций 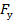
| ||
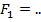 кН кН
| 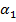 = =
| |||
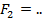 кН кН
| 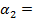
| |||
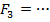 кН кН
| 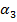 = =
| |||
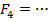 кН кН
| 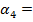
| |||
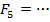 кН кН
| 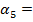
| |||
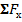
| 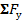
| |||
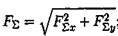
| ||||
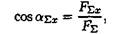
|
1.Вычертите каждую силу (таблица) на отдельной схеме координатных осей ОХ, ОУ.
2. Изобразите проекции силна оси ОХ и ОУ геометрически.
Рассчитайтедля каждой силы проекции FХ, FУ:FХ = Fcosα, Fy = Fsinα
3. Рассчитайтепроекцию равнодействующейсистемы сил на оси ОХ, ОУ
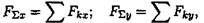
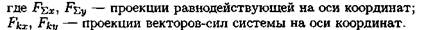
4. Рассчитайте равнодействующую системы сил 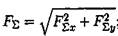
5. Рассчитайте угол равнодействующей с осью Ох 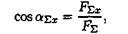 , где
, где 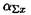 - угол равнодействующей с осью Ох.
- угол равнодействующей с осью Ох.
6. Определите аналитическим способом – находится ли данная система сил в равновесии:
Условие равновесия
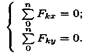
Рассчитать погрешность измерения
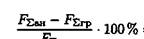 Результаты расчетов не должны отличаться более чем на 5 %
Результаты расчетов не должны отличаться более чем на 5 %
Задание 2 (с.140). Рассчитать алгебраическую сумму проекций всех сил на оси ОХ, ОУ(предварительно нанести на схему балки реакции опоры). Находится ли данная система в равновесии. Данные в таблице к заданию 1.
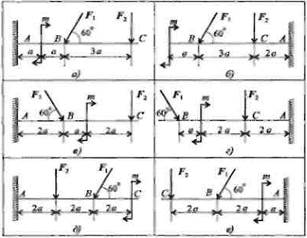
Рекомендации:
1. Нарисуйте схему по варианту, нанеся на нее данные размеров (а) и значение сил и моментов из таблицы.
2. Нанести на схему балки реакции опоры (R AХ, R AУ, М R ).
3. Нанесите, рассчитайте и соответственно просуммируйте проекции всех сил (F 1,F 2, R AХ, R AУ ) на оси:
проекция силы под углом к балке рассчитывается из прямоугольного треугольника через синус или косинус угла
4. Если суммы проекций на оси ОХ и ОУ равны нулю, то система находится в равновесии.
Приравнявая, полученные проекции сил на оси ОХ, ОУ к нулю, определите реакции опорR AХ, R AУ.
Пример 3. Груз подвешен на стержнях и находится в равновесии. Определить усилия
в стержнях. Дано таблица с. 134
 Рекомендации: см. [1] пр. 1 с. 14-15
Рекомендации: см. [1] пр. 1 с. 14-15
Задание 4. Определить реакции стержней АС и AD (рис. П1.3) с.134
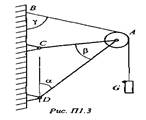
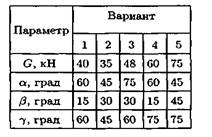
Вывод: ___________________________ (результат поставленных задач)
Рекомендованная литература
| 1. Олофинская В. П., Техническая механика. М. Инфра – 2014 |
| 2. Эрдеди А. А., Теоретическая механика. Сопротивление материалов. М. Высшая школа – 2014. |