Логистическая регрессия
Во многих приложениях наряду с классификацией объектов требуется ещё оценивать степень их принадлежности тому или иному классу или «степень уверенности» классификации. Это позволяет делать логистическая регрессия – распространенный статистический инструмент для решения задач регрессии и классификации. Иными словами, с помощью логистической регрессии можно оценивать вероятность того, что событие наступит для конкретного испытуемого (больной/здоровый, возврат кредита/дефолт и т.д.).
Логистическая регрессия – это разновидность множественной регрессии, общее назначение которой состоит в анализе линейной связи между несколькими независимыми переменными и зависимой переменной. Когда предсказываемых классов два, то говорят о бинарной логистической регрессии. В традиционной множественной линейной регрессии существует следующая проблема: алгоритм не «знает», что переменная отклика бинарна по своей природе.
Это неизбежно приведет к модели с предсказываемыми значениями большими 1 и меньшими 0.
Но такие значения вообще не допустимы для первоначальной задачи. Таким образом, множественная регрессия просто игнорирует ограничения на диапазон значений для y.
Для решения проблемы задача регрессии может быть сформулирована иначе: вместо предсказания бинарной переменной мы предсказываем непрерывную переменную со значениями на отрезке [0,1] при любых значениях независимых переменных. Это достигается применением логит-преобразования вида:
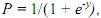
где P – вероятность того, что произойдет интересующее событие; e – основание натуральных логарифмов 2,71…; y – стандартное уравнение регрессии:
|
|
Существует несколько способов нахождения коэффициентов логистической регрессии. На практике часто используют метод максимального правдоподобия. Он применяется в статистике для получения оценок параметров генеральной совокупности по данным выборки. Основу метода составляет функция правдоподобия (likehood function), выражающая плотность вероятности (вероятность) совместного появления результатов выборки. Для поиска максимума, как правило, используется оптимизационный метод Ньютона, для которого здесь всегда выполняется условие сходимости. Для облегчения вычислительных процедур максимизируют не саму функцию правдоподобия, а е 
е логарифм. В результатах обычно выводят численное значение (–2*Log likehood) либо на каждом шаге алгоритма, либо на последнем шаге.
Бинарная логистическая регрессия эквивалента построению рейтинговой или балльной модели, т.к. если признак fj наблюдается у объекта х, то к сумме баллов добавляется вес aj.
Классификация производится путём сравнения набранной суммы баллов с пороговым значением. Благодаря свой простоте подсчёт баллов или скоринг (scoring) пользуется большой популярностью у экспертов в таких областях, как медицина, геология, банковское дело, социология, маркетинг и др.
Подготовка обучающей выборки
Для построения модели логистической регрессии готовится обучающая выборка так же, как это описано для нейросети. Но выходное поле может быть только дискретного типа и бинарное (т.е. количество уникальных значений по нему должно быть равно двум).
На этапе определения входов модели необходимо помнить, что естественное стремление учесть как можно больше потенциально полезной информации приводит к включению избыточных шумовых признаков. Экспериментально установлено, что для успешного обучения число примеров должно в несколько раз (примерно в 5) превосходить число входных признаков. Но даже если все признаки информативны, количества обучающих примеров может просто не хватить для надёжного определения коэффициентов регрессии при всех признаках. Когда данных мало, приходится искусственно упрощать структуру регрессионной модели, оставляя наиболее существенные признаки.
|
|