Для полей, подаваемых на входы, задается нормализация. Можно задать либо нормализацию битовой маской, либо нормализацию уникальными значениями (описание см. в разделе по нейросетям).
Для выходного поля (зависимой переменной) необходимо определиться с тем, что является отрицательным (negative), а что – положительным событием (positive). Это зависит от конкретной задачи. Например, если мы прогнозируем вероятность наличия заболевания, то положительным исходом будет класс «Больной пациент», отрицательным – «Здоровый пациент». И наоборот, если мы ходим определить вероятность того, что человек здоров, то положительным исходом будет класс «Здоровый пациент» и так далее. Отрицательное событие должно следовать в списке уникальных значений первым, положительное – вторым. По умолчанию они сортируются по алфавиту. Для переопределения типа события используйте окно Нормализация, вкладку Параметры нормализации.

Настройка обучающей выборки
Настройка обучающей выборки такая же, как для нейросети и других алгоритмов построения моделей.
Обучение логистической регрессионной модели
Под обучением понимается расчет коэффициентов регрессионной модели. В Deductor строится бинарная логистическая регрессия путем решения нелинейного уравнения итерационным методом Ньютона. Параметры обучения логистической модели следующие:
§ Максимальное число итераций – алгоритм расчета коэффициентов завершится, когда очередное значение логарифмической функции правдоподобия –2*Log likehood прекратит изменяться в пределах заданной точности. Если данная опция не включена, то ограничения на число итераций отсутствует.
§ Точность функции оценки – параметр влияет на количество итераций алгоритма до его успешной сходимости.
§ Порог отсечения – задача бинарной классификации будет решена на основе заданного порога отсечения для поля со значением рейтинга, по умолчанию порог равен 0,5.
В результате работы алгоритма на выходе обработчика к исходному набору данных добавляются два поля:
§ <Имя выходного поля> Рейтинг – значение выхода в уравнении логистической регрессии от 0 до 1;
§ <Имя выходного поля>_OUT – выходное поле, полученное на основе поля с рейтингом с использованием порога отсечения k: всем примерам, большим или равным k, приписывается положительный исход, остальным – отрицательный исход прогнозируемого события.
В самом простом случае в качестве порога можно взять значение 0,5. Однако при наличии некоторого критерия качества можно определить оптимальный порог (оптимальный балл). Это позволяет сделать специальный визуализатор ROC-анализа (см. одноименный раздел ROC- анализ). Также доступна для визуализации таблица сопряженности.
Пример
Продолжим пример об оценке кредитоспособности физических лиц, рассмотренный в пункте, посвященном нейронным сетям. Покажем, как при помощи логистической регрессии построить несложную скоринговую карту – список характеристик заемщика с их весами (баллами). Всех заемщиков можно разделить на два класса – кредитоспособных и некредитоспособных.
Поскольку в кредитовании общепринято, что чем выше кредитоспособность клиента, тем больше его рейтинговый балл, обозначим в обучающем множестве положительным исходом успешный возврат кредита, а отрицательным – дефолт по займу. Для лучшей интерпретации регрессионных коэффициентов всем качественным переменным рекомендуется делать нормализацию битовой маской по способу кодирования «Позиция бита», в этом случае для каждого уникального значения качественного признака будет подбираться свой коэффициент (балл). От фактора «Автомобиль» здесь откажемся. Тогда при кодировании качественной переменной «Образование» в уравнение регрессии будут введены 2 дополнительных независимых переменных. В итоге получим 7 переменных плюс 1 переменная для константы.
Откроем визуализаторы «Коэффициенты регрессии», «Таблица сопряженности» и «Что-если».

В первом визуализаторе мы наблюдаем по сути скоринговую карту. Помимо коэффициента для каждой регрессионной переменной в таблице рассчитывается отношение шансов (odds ratio), т.к. именно оно помогает интерпретировать модель.
Отношение шансов OR – это отношение вероятности того, что событие произойдет к вероятност того, что событие не произойдет: OR = p / (1 – p), где p – вероятность успеха.
В логистической регрессии коэффициенты xi дают не только веса признаков, но и обладают полезным свойством. Рассчитав exp(xi) для конкретной переменной, мы получим отношение шансов для этой переменной.
В нашем примере категориальный признак Образование имеет три веса: 1 при среднем образовании, 1,54 – при специальном и 1,71 – при высшем. Это значит, что у заемщика со специальным образованием шансы наступления того, что он окажется благонадежным, в 1,54 раза более вероятны, чем со средним. У заемщика с высшим образованием они еще выше (в 1,71 раза).
Для непрерывных переменных удобно рассчитать отношение шансов для заданного приращения переменной посредством вычисления exp(c·xi), где c – число единиц измерения. Например, для признака Срок проживания в регионе exp(10·0,0098) = 1,1, что означает: дополнительные 10 лет проживания в регионе увеличивают шансы возврата кредита в 1,1 раза.
Расчет рейтинга по такой скоринговой карте можно вести даже вручную. Но лучше воспользоваться инструментом «Что-если».

На диаграмме «Что-если» можно, к примеру, увидеть, как будет изменяться рейтинг этого заемщика с увеличением возраста:

Видно, что балльная модель демонстрирует линейную зависимость между возрастом и рейтингом, что в реальности встречается не всегда.
Оценить качество логистической регрессии как классификатора можно на основе таблицы сопряженности. По умолчанию порог отсечения равен 0,5.

В этой таблице сопряженности зафиксировано 18 случаев ложного обнаружения (заемщик признан благонадежным, тогда как по факту он «плохой») и 22 случая ложного пропуска («хорошему» клиенту было отказано). Доля верно классифицированных случаев составила чуть более 73%. Это не самый высокий показатель, и его, скорее всего, можно улучшить, подобрав оптимальную пороговую точку. Это позволяет сделать ROC-анализ (см. соответствующий раздел настоящего Руководства).
ROC-анализ
ROC-анализ позволяет провести оценку качества модели-классификатора, сравнить прогностическую силу нескольких моделей, определить оптимальную точку отсечения для отнесения объектов к тому или иному классу. При этом предполагается, что у классификатора имеются дополнительные параметры, позволяющие уже после проведенного обучения варьировать соотношение ошибок первого и второго рода. В частности, логистическая регрессия (см. одноименный раздел настоящего Руководства) удовлетворяет таким требованиям, т.к. модель на ее основе имеет выходное поле рейтинга, которое можно интерпретировать как вероятность положительного исхода интересующего события.
В основе ROC-анализа лежит построение графиков – ROC-кривых. ROC-кривая (Receiver Operator Characteristic) – кривая, которая наиболее часто используется для представления результатов бинарной классификации в машинном обучении. Название пришло из систем обработки сигналов. Поскольку классов два, один из них называется классом с положительными исходами, второй – с отрицательными. ROC-кривая показывает зависимость количества верно классифицированных положительных примеров от количества неверно классифицированных отрицательных примеров. В терминологии ROC-анализа первые называются истинно положительным, вторые – ложно отрицательным множеством. Как уже говорилось выше, у классификатора имеется некоторый параметр, варьируя который, мы будем получать то или иное разбиение на два класса. Этот параметр часто называют порогом, или точкой отсечения (cut-off value). В зависимости от него будут получаться различные величины ошибок I и II рода.
Для понимания сути ошибок I и II рода рассмотрим четырехпольную таблицу сопряженности, которая строится на основе результатов классификации моделью и фактической (объективной) принадлежности примеров к классам.

· TP (True Positives) – верно классифицированные положительные примеры (так называемые истинно положительные случаи);
· TN (True Negatives) – верно классифицированные отрицательные примеры (истинно отрицательные случаи);
· FN (False Negatives) – положительные примеры, классифицированные как отрицательные (ошибка I рода). Это так называемый «ложный пропуск», когда интересующее нас событие ошибочно не обнаруживается (ложноотрицательные примеры);
· FP (False Positives) – отрицательные примеры, классифицированные как положительные (ошибка II рода). Это ложное обнаружение, т.к. при отсутствии события ошибочно выносится решение о его присутствии (ложноположительные случаи).
Что является положительным событием, а что – отрицательным, зависит от конкретной задачи.
Например, если мы прогнозируем вероятность наличия заболевания, то положительным исходом будет класс «Больной пациент», отрицательным – «Здоровый пациент». И наоборот, если мы ходим определить вероятность того, что человек здоров, то положительным исходом будет класс «Здоровый пациент» и так далее.
При анализе чаще оперируют не абсолютными показателями, а относительными – долями (rates), выраженными в процентах:
Доля истинноположительных примеров (True Positives Rate):

Доля ложноположительных примеров (False Positives Rate):

Введем еще два определения: чувствительность и специфичность модели. Ими определяется объективная ценность любого бинарного классификатора.
Чувствительность (Sensitivity) – это и есть доля истинно положительных случаев:

Специфичность (Specificity) – доля истинно отрицательных случаев, которые были правильно идентифицированы моделью:

Модель с высокой чувствительностью часто дает истинный результат при наличии положительного исхода (обнаруживает положительные примеры). Наоборот, модель с высокой специфичностью чаще дает истинный результат при наличии отрицательного исхода (обнаруживает отрицательные примеры). Если рассуждать в терминах медицины – задачи диагностики заболевания, где модель классификации пациентов на больных и здоровых называется диагностическим тестом, то получится следующее:
· чувствительный диагностический тест проявляется в гипердиагностике – максимальном предотвращении пропуска больных;
· специфичный диагностический тест диагностирует только доподлинно больных. Это важно в случае, когда, например, лечение больного связано с серьезными побочными эффектами и гипердиагностика пациентов не желательна.
ROC-кривая получается следующим образом: для каждого значения порога отсечения, которое меняется от 0 до 1 с шагом dx (например, 0.01) рассчитываются значения чувствительности Se и специфичности Sp. Строится график зависимости: по оси Y откладывается чувствительность Se, по оси X – (100% – Sp) (сто процентов минус специфичность).
Пример ROC-кривой приведен на рисунке. График часто дополняют прямой y = x.

Для идеального классификатора график ROC-кривой проходит через верхний левый угол, где доля истинно положительных случаев составляет 100% или 1,0 (идеальная чувствительность), а доля ложноположительных примеров равна нулю. Поэтому чем ближе кривая к верхнему левому углу, тем выше предсказательная способность модели. Наоборот, чем меньше изгиб кривой и чем ближе она расположена к диагональной прямой, тем менее эффективна модель.
Диагональная линия соответствует «бесполезному» классификатору, т.е. полной неразличимости двух классов.
При визуальной оценке ROC-кривых расположение их относительно друг друга указывает на их сравнительную эффективность. Кривая, расположенная выше и левее, свидетельствует о большей предсказательной способности модели. Так, на рисунке ниже две ROC-кривые совмещены на одном графике. Видно, что модель «A» лучше.

Визуальное сравнение ROC-кривых не всегда позволяет выявить наиболее эффективную модель. Своеобразным методом сравнения ROC-кривых является оценка площади под кривыми.
Теоретически она изменяется от 0 до 1,0, но поскольку модель всегда характеризуется кривой, расположенной выше положительной диагонали, то обычно говорят об изменениях от 0.5 («бесполезный» классификатор) до 1,0 («идеальная» модель). Эта оценка может быть получена непосредственно вычислением площади под многогранником, ограниченным справа и снизу осями координат и слева вверху экспериментально полученными точками. Численный показатель площади под кривой называется AUC (Area Under Curve). Вычислить его можно, например, с помощью численного метода трапеций. Если AUC ≥ 0,8, то можно говорить о том, что модель обладает высокой прогностической силой.
Идеальная модель обладает 100% чувствительностью и специфичностью. Однако на практике добиться этого невозможно, более того, невозможно одновременно повысить и чувствительность и специфичность модели. Компромисс находится с помощью порога отсечения, т.к. пороговое значение влияет на соотношение Se и Sp. Можно говорить о задаче нахождения оптимального порога отсечения (optimal cut-off value).
Порог отсечения нужен для того, чтобы применять модель на практике: относить новые примеры к одному из двух классов. Для определения оптимального порога нужно задать критерий его определения, т.к. в разных задачах присутствует своя оптимальная стратегия. Существует, по крайней мере, 2 варианта:
· Требование максимальной суммарной чувствительности и специфичности модели, т.е.

· Требование баланса между чувствительностью и специфичностью, т.е. когда Se »Sp:

Пример
В Deductor ROC-анализ является визуализатором, доступным после обработчика «Логистическая регрессия». Проведем ROC-анализ балльной модели оценки кредитоспособности физических лиц, построенной в разделе «Логистическая регрессия».
Проецируя определения чувствительности и специфичности на оценку кредитоспособности (скоринг), можно заключить, что скоринговая модель с высокой специфичностью соответствует консервативной кредитной политике (чаще происходит отказ в выдаче кредита), а с высокой чувствительностью – политике рискованных кредитов. В первом случае минимизируется кредитный риск, связанный с потерями ссуды и процентов и дополнительными расходами на возвращение кредита, а во втором – коммерческий риск, связанный с упущенной выгодой.
При первоначальном открытии визуализатора в Deductor рисуется график ROC-кривой, вычисляется оптимальная точка по способу максимума чувствительности и специфичности («точка максимума») и площадь под кривой AUC.
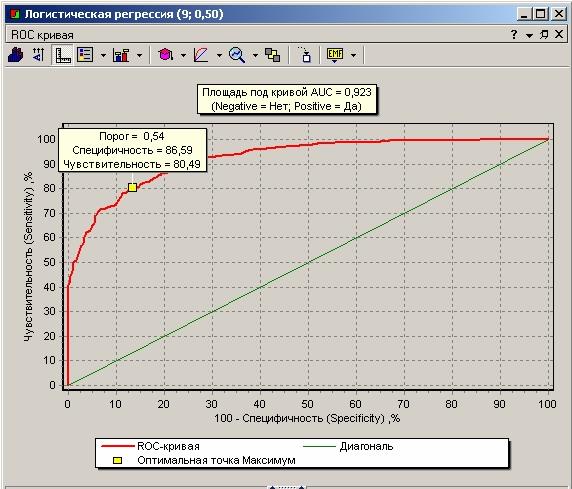
Оптимальный порог («точка максимума») в нашем случае оказался равен 0,54, а не 0,5, каким он устанавливается по умолчанию. В этой точке чувствительность превышает 80%, что означает следующее: 80% благонадежных заемщика будут подтверждены моделью. Специфичность равна 86,6%, следовательно, 13,4% недобросовестных заемщиков получат одобрение в выдаче кредита (кредитный риск). Это хороший показатель, свидетельствующий о том, что скоринговая модель соответствует умеренной кредитной политике, но если такая ситуация не устраивает, то можно увеличить величину порога или найти такую точку на ROC-кривой, в которой будет достигаться требуемое соотношение чувствительности и специфичности.
Баланс между чувствительностью и специфичностью («точка баланса») получается в точке 0,44 (Se и Sp около 82%). Точку баланса можно наблюдать на графике кривой баланса.
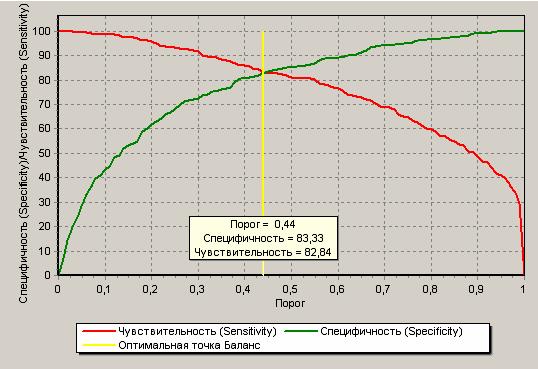
Для переключения между графиками используйте кнопки  и
и  . Для переключения между критерием оптимальности для точки (максимум, баланс, текущая) нужно нажать кнопку
. Для переключения между критерием оптимальности для точки (максимум, баланс, текущая) нужно нажать кнопку  на панели.
на панели.
Тип события при построении ROC-кривой берется из установок нормализации логистической регрессии и выводится в легенде графика под значением AUC. В данном примере отрицательному исходу (Negative) соответствует «плохой» заемщик (займ не был возвращен), а положительному (Positive) – займ возвращен.
Определять значение оптимального порога отсечения имеет смысл на обучающемся или общем множестве, т.е. на тех данных, которые принимали участие в расчете коэффициентов. Поэтому на тестовом множестве, если оно рассматривается отдельно (кнопка  ), оптимальные точки не рассчитываются и не показываются на ROC-кривой и в детализации.
), оптимальные точки не рассчитываются и не показываются на ROC-кривой и в детализации.