Изучение колебаний связанных маятников
(с использованием установки Кобра 3)
Учебно-методическое пособие
к лабораторной работе № 1.6
Владивосток
УДК53(076.5)
ББК 22.36
О-60
О-60 Изучение колебаний связанных маятников (с использованием установки Кобра3) Учебно-методическое пособие к лабораторной работе № 3.60рпо дисциплине «физический практикум»/ сост. В.В. Короченцев, В.С. Печников, В.В. Зауткин - Владивосток: 2014.-10 с.
Пособие, подготовленное на кафедре общей физики Школы естественных наук ДВФУ, содержит методические указания к выполнению лабораторной работы по механике с целью экспериментального изучения колебаний связанных маятников (с использованием установки Кобра3).
Для студентов Дальневосточного федерального университета.
УДК 53(076.5)
ББК 22.36
© Короченцев В.В.
Печников В.С.
Зауткин В.В.
Колебания двух связанных маятников
Для одного несвязанного маятника или для двух связанных маятников, отклоненных на одинаковые углы в одну сторону справедливо основное уравнение динамики вращательного движения твердого тела:
I e = mgrφ, (1)
где mglφ – момент силы тяжести, I – момент инерции,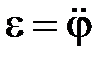 
– угловое ускорение. Решение этого уравнения известно
φ (t) = φmax cos ω0t,
где ω02 = mgl/ I
Два маятника, связанные пружиной, которые могут совершать колебания в вертикальной плоскости, проходящей через точки подвеса этих маятников, являются системой с двумя степенями свободы, т.к. состояние системы полностью описывается двумя независимыми параметрами – углами φ1 и φ 2 отклонения маятников.
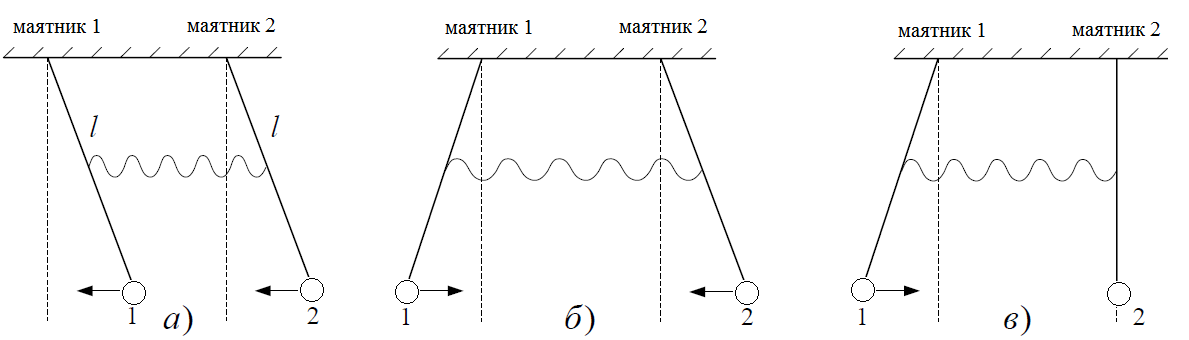
Рисунок 1. Системы связанных маятников
Если маятники вначале отклоняют в одну сторону и отпускают (рис.1, а), то пружинка не деформируется и не влияет на синхронные (с равным периодом) и синфазные (в одинаковых фазах, "в такт") колебания обоих маятников. Частота этих колебаний обычна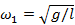 
. Это частота так называемой первой нормальной моды связанных колебаний маятников (нормальной модой называют "чистую" гармонику, т.е. гармоническое колебание с постоянной амплитудой и неизменной частотой). Если маятники вначале отклонить в разные стороны и отпустить (рис.1, б), то колебания будут происходить в противофазе (встречно). При этом пружинка максимально деформируется, производя дополнительную упругость в системе, дополнительную возвращающую силу. Дополнительная упругость приводит к увеличению частоты колебаний, поэтому такие колебания происходят с частотой ω02>ω01; ω 02 - это частота второй нормальной моды.
|
|
Если маятники вначале отклонить на разные углы и отпустить (рис.1, в), то пружинка будет деформироваться в разные моменты времени по-разному: от нулевого растяжения (случай 1 а) до максимального (случай 1 б). Результирующее колебание представится суперпозицией двух колебаний: с частотой ω01, и с частотой ω02 - так реально возникают биения двух нормальных мод колебаний).
Поведение связанных маятников интересно рассмотреть с энергетической точки зрения. Если при t=0 вся энергия была сосредоточена в маятнике 1, а маятник 2 покоился (рис.1, в), то с течением времени в результате связи через пружинку энергия постепенно передается от маятника 1 к маятнику 2 до тех пор, пока вся энергия не окажется в маятнике 2 (при этом маятник 1 остановится). Затем процесс обмена энергии повторяется от маятника 2 к маятнику 1 и так далее - происходят биения. Таким образом, биения сопровождаются процессом обмена энергией между двумя гармоническим осцилляторами (колебательными системами, в рассмотренном примере - маятниками) с близкими собственными частотами.
|
|
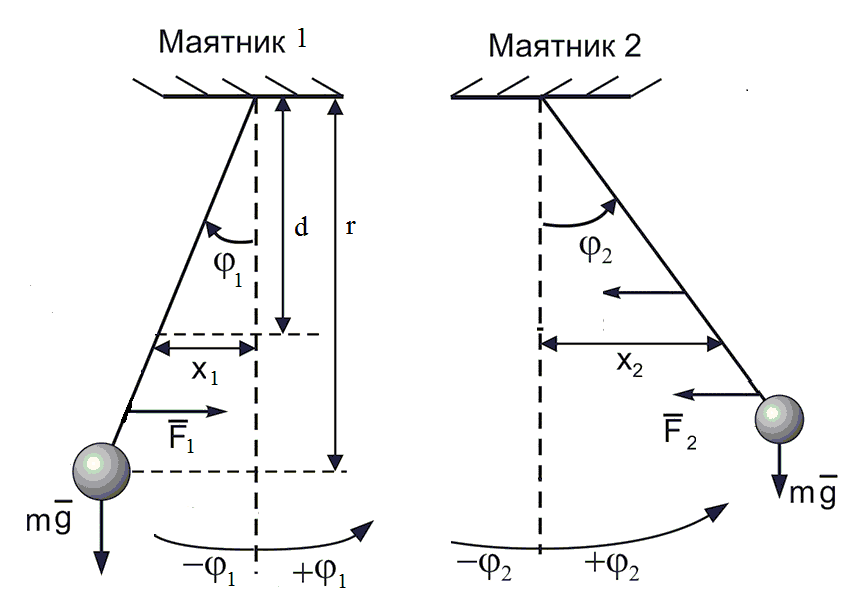
Рисунок 2. Схема связанных маятников (φ1 ≠ φ2)
Рассмотрим систему связанных маятников, отклоненных в разные стороны (колебания «в противофазе») рис.2. Приняты следующие обозначения: m – масса одного маятника без учета массы пружины; r – расстояние от центра масс маятника до точки подвеса; d – расстояние от точки прикрепления пружины до точки подвеса; φ1 и φ2 – углы отклонения от положения равновесия первого и второго маятника соответственно. Относительно точки подвеса вращательные моменты создают две силы: сила тяжести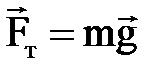 
и сила упругости соединительной пружины Fупр = –кΔх, к – жесткость пружины. Моменты этих сил соответственно равны:
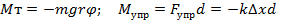
Так как х1 и х2 – отклонения точек прикрепления пружины от своего положения равновесия (рис.2), то деформация пружины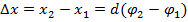 
и момент силы упругости 
.
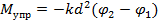С учетом сказанного уравнения движения маятников можно записать в виде:
)
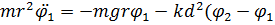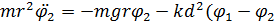) (2)
Введем коэффициент связи системы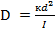 
. Тогда по (2) получаем:
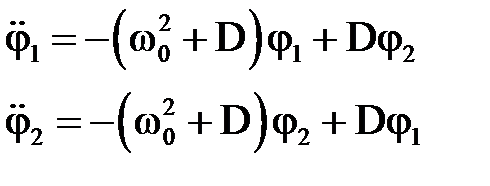(3)
Напомним, что эти уравнения справедливы при малых углах отклонения маятников. Решение системы (3) определяется начальными условиями. В лабораторной работе могут быть использованы три случая.
1. Маятники отклонены на одинаковый угол в одну сторону (колебания «в фазе»). В этом случае пружина не деформируется, упругой силы и ее момента нет, оба маятника колеблются с одинаковой частотой ω0 = ω01= ω02. В системе (2) φ1 = φ2= φ, φ1 – φ2 =0, и оба уравнения системы (2) превращаются в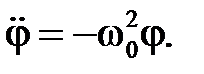 
|
|
2. Маятники отклонены в разные стороны на одинаковый угол (колебания «в противофазе»). В этом случае в начальный момент φ2 = -φ1 и φ2 – φ1=2φ. Для обоих маятников будут одинаковые уравнения:
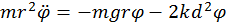
Откуда
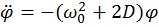
Т.е. маятники и в этом случае совершают гармонические колебания с частотой
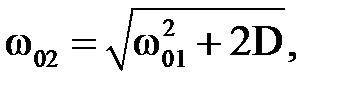или
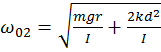
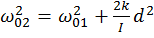
Обратите внимание, что в этом случае частота колебания маятников больше, чем частота их колебаний в несвязанном состоянии. Переходя от углов к смещению маятников от положения равновесия х, уравнение колебаний маятников имеют вид:
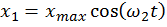
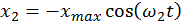
3.Биения связанных маятников
Удержим один из маятников в вертикальном положении (φ = 0), а другой отклоним на угол φ, в момент t = 0 отпустим маятники. Получаем начальные условия φ1 = 0, φ2 = φ, φ2 - φ1 = φ. Тогда решение системы (2) будет в виде
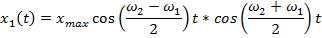
(4)
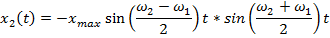
Т.о., при биениях каждого маятника частота колебаний близка к собственной частоте каждого маятника (ω01 + ω02)/2, а частота биений определяется силой связи маятников D.
Выполнение работы
Коэффициент жесткости пружины к = 3 Н/м.
1. Определите период и частоту собственных частот колебаний несвязанных маятников. Для этого отклоните оба маятника из положения равновесия в одну сторону на 5о-10о и измерьте с помощью секундомера время 20-30 колебаний. Вычислите период То и частоту ωо. Опыт повторите не менее 5 раз. Сравните получившиеся результаты с данными, полученными на компьютере с помощью оборудования «Cobra3».
Запустите программу измерений «measure». Выберете «Прибор» → «Кобра 3: универсальный измеритель» → «Записи измерений». На всплывающем меню должны быть выставлены параметры, приведенные на рис. 3.
2. Измерение периода «синфазных» нормальных колебаний.
Отклоните маятники из положения равновесия на 5—10º и отпустите их. После установления равномерного колебательного процесса (через≈5-10 с) начните измерения, нажав на кнопку «далее». Процесс записи колебаний должен происходить не менее двух-трёх минут. При запуске измерений секундомер включается автоматически. Одновременно записываются колебания обеих маятников. После команды завершения измерений на экране появляются графики колебаний. Выбирая аналоговые входы 1 или 2 (U1, U2), можно наблюдать на экране монитора графики колебаний каждого маятника в отдельности.
По графикам несколько раз (не менее 5) определите период колебаний Т0 для каждого маятника.
3. Вычислите собственную частоту колебаний несвязанных маятников: ω0 = 2π/Т0 (по средним значениям Т0). Измерение периода противофазных «антифазных» нормальных колебаний.
Отведите маятники в разные стороны на 50 и отпустите. Измерьте секундомером период колебаний. Рассчитайте частоту колебаний ω02.
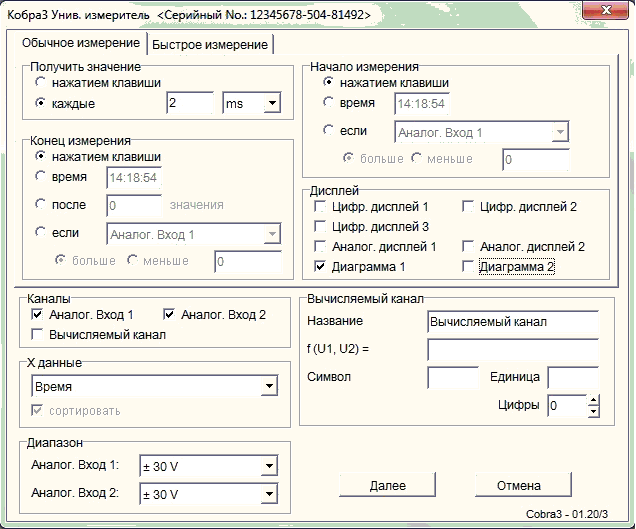
Рисунок 3. Окно программы – параметры измерений
4. Изучение произвольного режима колебаний связанных маятников (режим "биений").
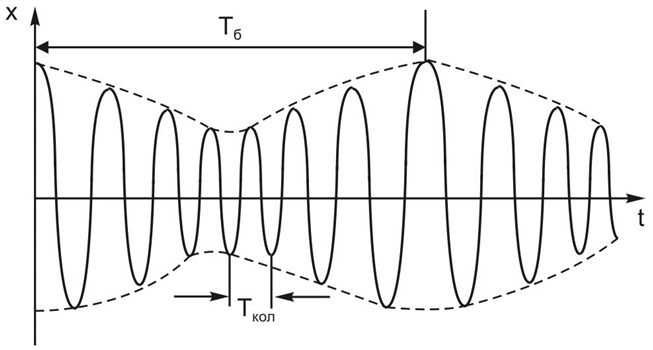
Найдите период колебаний Т для одного из маятников при биениях. Для возникновения биений перед запуском системы один из маятников удерживайте в положении равновесия, а второй – отклоните на небольшой угол 50—100. Затем маятники одновременно отпустите. Измерьте время десяти колебаний.
Измерьте период биений Тб. Для этого с помощью секундомера измерьте время между двумя последовательными остановками в движении одного из маятников. Проделайте опыт не менее пяти раз, вычислите среднее.
Сравните получившиеся результаты с данными, полученными на компьютере с помощью оборудования «Cobra3». Получите график биений с помощью с помощью оборудования «Cobra3». Сравните энергетические графики биений.
Определите частоты ω1 и ω2 двух колебаний, из которых складывается результирующее колебание каждого из маятников.
По формулам рассчитайте ω1 и ω2. Используя графики колебаний, несколько раз (не менее 5) определите на разных этапах движения период колебаний Ткол и период биений Тб. Полученные значения усредните.
Проделайте аналогичные измерения для трех разных расстояний d. Рекомендуется взять d = 30, 40, 50, см. Результаты представьте в таблице, указав d, Ткол, Тб, ω1, ω2.
5. Определите коэффициент связи колебательной системы
- рассчитайте коэффициент связи системы D для разных длин сцепления d. Используйте значения d, для которых проводился опыт. Результаты представьте в таблице, указав d1, к, m, l, ω0, D.
- Используя данные, полученные в упр. 3, рассчитайте коэффициент связи D через собственные частоты колебаний связанной системы ω01 и ω02 для всех длин сцепления d1. коэффициент связи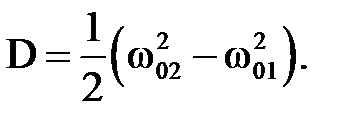 
Результаты представьте в виде таблицы, указав d 1, ω01, ω02, D.
Контрольные вопросы
1. Основное уравнение динамики вращательного движения твердого тела
2. Моды колебаний.
3. Уравнения движения связанных маятников.
4. Виды движения связанных маятников (в «фазе», в «противофазе»)
5. «Биения» связанных маятников.
6. Энергетическая интерпретация «биений» связанных маятников.
7. Закон Гука.
8. Моменты сил тяжести и упругости.
9. Коэффициент связи маятников.
Литература
1. Савельев И.В. Курс физики: Том 1. Механика.: Уч. пособие. Т.1. М.. 4-е изд., стер. – СПб.: Издательство «Лань», 2008г.-352с:
2. Трофимова Т.И. Курс физики. – М.: Высшая школа, 2002-2009.
3. Стрелков, С.П. Механика./ С.П. Стрелков. Спб.:«Лань»., 2005.-560с.
4.Зисман, Г.А., Курс общей физики, том 1. Механика. Изд. 7-е, стер.. - СПб: «Лань»., 2007. - 340 c
5. Алешкевич В.А., Деденко Л.Г., Караваев В.А. Курс общей физики. Механика https://e.lanbook.com/view/book/2384/
Учебно-методическое пособие
Изучение колебаний связанных маятников
(с использованием установки Кобра3)
Учебно-методическое пособие
к лабораторной работе № 1.6
Составители
Короченцев Владимир Владимирович
Печников Владимир Степанович
Зауткин Валерий Васильевич
В авторской редакции
Формат 60х84 1/16
Усл. печ. л. 0,70. Уч.-изд.л. 0,75. Тираж 100 экз.
Издательский дом Дальневосточного федерального университета
690950, Владивосток, Пушкинская, 10.
Отпечатано на кафедре общей физики ШЕН ДВФУ
690950, Владивосток, о.Русский, нп. Аякс, кампус ДВФУ.