Линейные операторы и линейные функционалы

Пусть 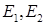– линейные нормированные пространства.

Определение: Линейным оператором, действующим из 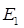в 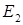, называется отображение 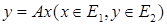, удовлетворяющее условию: 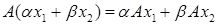для любых , .

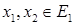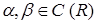Будем говорить, что в (вещественной или комплексной линейной системе) определен функционал 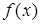, если каждому элементу 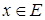поставлено в соответствие некоторое вещественное (комплексное) число .

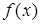Определение: Линейный оператор, действующий из Е в Е₁, называется ограниченным, если он определен на всем Е и каждое ограниченное множество переводит снова в ограниченное.

Определение: Оператор А называется непрерывным в точке 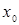, если для любой последовательности 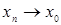выполняется условие .

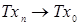Определение: Оператор А называется непрерывным, если он непрерывен в каждой точке пространства Е.

Теорема: Для того, чтобы линейный оператор 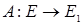был непрерывным, необходимо и достаточно, чтобы он был ограничен.

Доказательство.

1. Пусть оператор А неограничен. Тогда существует М 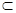Е – ограниченное множество, такое, что множество АМ 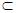Е₁ не ограничено. Следовательно, в Е₁ найдется такая окрестность нуля V, что ни одно из множеств 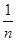АМ не содержится в V. Но тогда существует такая последовательность х_n 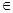M, что ни один из элементов 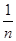Ах_n не принадлежит V и получаем, что 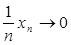в Е, но 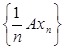не сходится к 0 в Е; это противоречит непрерывности оператора А.

2. Если оператор А не непрерывен в точке 0, то в Е₁ существует такая последовательность 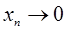, что Ах_n не стремится к 0. При этом последовательность 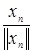ограничена, а последовательность 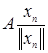не ограничена. Итак, если оператор А не непрерывен, то А и не ограничен.

Определение: Оператор называется конечномерным, если он ограничен и переводит данное пространство в конечномерное.

Определение: Функционал 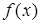называется линейным, если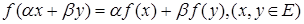

Линейный функционал – это частный случай линейного оператора.

([1], стр. 217), ([1], стр. 125)

Примеры линейных функционалов:

1. Пусть 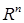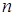– мерное арифметическое пространство с элементам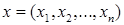и и 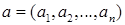– произвольный набор из 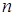– фиксированных чисел. Тогда 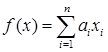является линейным функционалом.

2. Пример линейного функционала в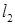

Пусть 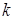– фиксированное целое положительное число. Для каждого 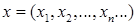из 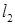положим 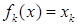. Таким образом 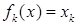является линейным функционалом в .

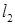Сопряженные операторы

Определение: Совокупность всех непрерывных линейных функционалов, определенных на некотором линейном нормированном пространстве , образует линейное пространство, которое называется пространством, сопряженным с , и обозначается

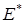
Рассмотрим непрерывный линейный оператор 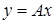, отображающий линейное топологическое пространство в такое же пространство 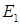. Пусть 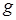– линейный функционал, определенный на 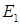, т. е. .

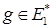Применим функционал 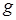к элементу 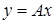. Функционал 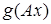есть непрерывный линейный функционал, определенный на 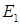. Обозначим его через 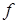. Функционал 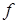есть, таким образом, элемент пространства 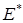(сопряженное с ). Каждому функционалу 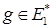мы поставили в соответствие функционал 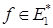, т.е. получили некоторый оператор, отображающий 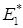в 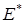. Этот оператор называется сопряженным к оператору 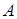и обозначается 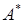. Обозначив значение функционала 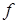на элементе 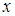символом 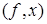, получим, что 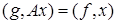, или .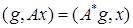

Это соотношение можно принять за определение сопряженного оператора. ([1], стр. 229)

Компактные операторы