Как известно, в процессах и явлениях природы энергия не исчезает и не возникает, она лишь переходит из одной формы в другую в эквивалентных количествах. Это – всеобщий закон сохранения и превращения энергии. Его частным случаем применительно к тепловым явлениям выступает первый законтермодинамики. Он характеризует баланс энергии в процессе, т. е. количественную сторону превращения энергии.
Пусть к некоторому рабочему телу (в расчёте на 1 кг) подводится бесконечно малое количество теплоты d q, вследствие чего прирастает его температура d T и удельный объём d v, т. е. возрастает на величину d u внутренняя энергия тела. Но при расширении рабочего тела совершается механическая работа d l против сил внешнего сопротивления (давления). Так как никаких других изменений в системе не происходит, то по закону сохранения энергии
. (4.4)
Это уравнение является математическим выражением Первого закона термодинамики. Рассмотрим некоторые частные случаи.
Первый случай Процесс в отсутствие теплообмена (адиабатный),
d q = 0. Формально из уравнения (4.4) имеем d l = – d u, т. е. работа расширения в адиабатном процессе может совершаться только за счёт уменьшения внутренней энергии; и наоборот, адиабатное сжатие рабочего тела извне приводит к возрастанию внутренней энергии, т. е. к его разогреву, как видно из рисунка 4.2.
Рисунок 4.2 – Разогрев системы в адиабатном процессе
Второй случай. Процесс при постоянном объёме рабочего тела (изохорный), d l = 0. Для него по рисунку 4.3 имеем d q = d u, т. е. подведённая извне теплота целиком расходуется на повышение внутренней энергии данной системы.
Рисунок 4.3 – Разогрев системы в изохорном процессе
|
|
Третий случай. Процесс при постоянном значении внутренней энергии, d u = 0. В этом случае d q = d l, т. е. вся подведённая извне теплота превращается в эквивалентное ей количество механической работы расширения против внешних сил (рисунок 4.4).
Теплоёмкость
Величина отношения количества теплоты d Q, полученного телом при бесконечно малом изменении его состояния, к вызванному изменению температуры d t называется теплоёмкостью тела (С) в данном процессе или на 1 кг рабочего тела
, (4.5)
где с – удельная теплоёмкость.
Рисунок 4.4 – Работа системы при подводе теплоты
В разных процессах нагрев тела на 1 °С требует разного количества теплоты:
– теплоёмкость в изобарном процессе (при постоянном давлении рабочего тела) cp = (d q/ d t) p=const;
– теплоёмкость в изохорном процессе (при постоянном объёме рабочего тела) cv = (d q/ d t) v=const.
Между теплоёмкостями cp и cv существует вполне определённая связь:
– идеальный газ (формула Майера) – cp = cv + R;
–реальный газ – cp – cv > R;
– жидкость – cp » cv.
Обычно значения теплоёмкостей определяются экспериментально и задаются таблично.
Энтальпия (I)
Это ещё одна функция состояния, определяемая как сумма внутренней энергии U и произведения (p × V), Дж, или удельная энтальпия, Дж/кг,
i = u + p × v.
Физический смысл энтальпии – это общее количество энергии (теплоты и работы), которое должно быть подведено к телу, чтобы перевести его из начального состояния в заданное. Изменение энтальпии в любом процессе определяется только начальным и конечным состояниями и не зависит от характера процесса.
|
|
Энтальпия, внутренняя энергия и теплоёмкость, относятся к калорическим свойствам вещества.
В изобарном процессе, характерном для теплоэнергетики и холодильной техники, подведённая (или отведённая) теплота расходуется только на повышение (понижение) энтальпии, q = i2 – i1. Поэтому для практических расчётов удобны таблицы (или построенные на их основе диаграммы) энтальпии. Малые изменения энтальпии и температуры связаны соотношением 
.
Реально же конечное приращение энтальпии D i определяется зависимостью
.
Энтропия (S)
Это функция состояния термодинамической системы. Удельная энтропия s (на 1 кг рабочего тела), кДж/(кг×К) определяется из дифференциального уравнения как отношение бесконечно малого приращения теплоты d q к абсолютной температуре T:
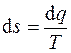. (4.6)
Сама удельная энтропия находится интегрированием:
.
Постоянная интегрирования s o= 0 при Т = 0 К.
Энтропия в тепловых явлениях играет такую же роль, как заряд в электрических явлениях. В представлении энтропии своеобразным термическим зарядом и состоит её физический смысл.
Состояние термодинамической системы может быть изображено точкой на весьма удобной в расчётах T, s - диаграмме. Процесс, как и в случае p,v- диаграммы, определяется траекторией этой точки от начального состояния к конечному состоянию (рисунок 4.5).
Рисунок 4.5 – Изменение состояний системы на T, s -диаграмме
Размер элементарной площадки под кривой процесса, в соответствии с определением (3.6), есть элементарная теплота d q = T d s.
Тогда вся площадь под кривой Т оказывается равной q:
|
|
. (4.7)
Здесь теплота процесса выражается через энтропию.
Аналогия структур выражений (4.3) и (4.7) показывает, что изменение энтропии также характеризует теплоту процесса, как изменение объёма – работу расширения.
Поскольку всегда Т > 0, то из определения (4.6) следует, что приращения энтропии и теплоты имеют одинаковый знак, т. е. по характеру изменения энтропии можно судить о направленности теплообмена системы со средой.