Известны три механизма переноса теплоты от одного тела к другому.
Теплопроводность (термодиффузия). Реализуется на микрофизическом уровне и определяется тепловым движением молекул. Позволяет предсказывать температурные поля и тепловые потоки в неоднородно нагретом теле или в системе тел, находящихся в прямом контакте и имеющих разные температуры. Действует во всех средах: газах, жидкостях и твёрдых телах.
Конвекция. Внешним воздействием создаётся упорядоченное (организованное) движение больших масс жидкости или газа вдоль поверхности рассматриваемой термодинамической системы. Эвакуация теплоты, переданной от горячей (холодной) стенки осуществляется макроскопическими объёмами движущейся среды. Конвективный механизм более эффективен по сравнению с теплопроводностью, что позволяет существенно интенсифицировать процесс теплопереноса. Конвекцию (макрофизический уровень теплопереноса) можно использовать только в жидкости или газе.
Излучение (тепловая радиация). Это бесконтактный механизм передачи теплоты. Он заключается в преобразовании внутренней энергии тела в энергию электромагнитных колебаний, её переносе через промежуточную среду и обратном преобразовании лучистой энергии в теплоту в другом теле – приёмнике. Перенос теплоты радиацией эффективен лишь в газовой среде (воздух, вакуум).
Согласно второму закону термодинамики самопроизвольный процесс переноса теплоты возникает под действием разности температур и направлен в сторону менее нагретого тела. Отмеченные выше механизмы обычно действуют одновременно и в совокупности определяют интенсивность теплопереноса. Количественная характеристика эффективности процесса теплопереноса – плотность теплового потока q, Вт/м2, определяет количество теплоты (Дж), прошедшей через единицу поверхности (м2) в единицу времени (с). Напомним, что 1 Дж/с = 1 Вт. Количество теплоты Q, прошедшей за произвольный отрезок времени t через произвольную поверхность теплообмена F, есть Q = q × F ×t, Дж.
Дадим основные определения и расчётные зависимости для отдельных механизмов теплопереноса и их совокупности – сложного теплообмена, чаще называемой теплопередачей.
Теплопроводность
Основная зависимость теплопроводности (закон Фурье) Вт/м2:
q = –l· grad t, (4.9)
т. е. вектор плотности теплового потока q пропорционален градиенту температуры; величина l, Вт/(м×K), согласующая размерности q и t, называется коэффициентом теплопроводности вещества. Знак минус показывает, что тепловой поток направлен в сторону уменьшения температуры. Уравнение теплопроводности (4.9) получено как эмпирическое обобщение. Коэффициент теплопроводности l, относящийся к числу индивидуальных свойств вещества, нелинейно зависит от температуры и обычно задаётся в табличной форме. Значения l сильно различаются для газов, жидкостей и твёрдых тел: у воздуха l~0,023; у дерева l~0,3; у воды l~0,6; у льда l~2,2; у меди l~380.
Простейшим и одновременно характерным объектом анализа полей (распределений) температур является плоская стенка толщиной d (рисунок 4.7), у которой заданы значения температур на границах t с1и t с2, а также коэффициент теплопроводности l, который в диапазоне [ t 1, t 2] можно считать постоянным.

Рисунок 4.7 – Распределение температуры в плоском теле:
t с1и t с2 – температуры на поверхностях стенки 1 и 2; d – толщина стенки; q – удельный тепловой поток через стенку
В одномерном случае уравнение (4.9) принимает такой вид:
 . (4.10)
. (4.10)
В стационарных условиях, когда энергия не расходуется на нагрев, плотность теплового потока неизменна по толщине стенки, q = const. При этом предположении интегрирование дифференциального уравнения (4.10) с разделяющимися переменными (в соответствующих пределах) даёт
 . (4.11)
. (4.11)
Таким образом, тепловой поток через плоскую стенку прямо пропорционален перепаду температур на границах и обратно пропорционален её толщине. По этой формуле можно также определить эмпирическое значение d, если суметь каким-либо образом измерить тепловой поток q и разность температур на поверхностях пластины.
Величина отношения d/l, (м2×K)/Вт носит название термического сопротивления и обозначается R с. Тогда выражение (4.11) примет вид
 , (4.12)
, (4.12)
аналогичный закону Ома в электротехнике, если силе тока поставить в соответствие тепловой поток, а разности потенциалов – температурный напор (t с1– t с2).
В практических расчётах часто приходится иметь дело с многослойной стенкой (один из слоёв – та или иная тепловая изоляция). Формула (4.12) для неё остаётся в силе, если термическое сопротивление R с подсчитывается как сумма термических сопротивлений каждого из слоёв, т. е.
 .
.
Наряду с плоской стенкой (ограждение крытого вагона) в хладотранспорте встречаются цилиндрическая (например, у трубопровода или вагона-цистерны), сферическая (форма многих скоропортящихся грузов) и т. д. Соответствующие формулы для расчёта q в них можно найти в справочниках по теплопереносу.
Конвективный теплообмен
Во многих устройствах перемещающиеся газообразные и жидкие среды нагреваются или отдают своё тепло, взаимодействуя с поверхностью твёрдого тела. В хладотранспорте – это воздух холодильной камеры, приводимый в движение вентиляторами-циркуляторами; хладагент в трубах испарителей и конденсаторов; наружные стены вагонов отепляемые или охлаждаемые потоками воздуха при движении состава или вследствие обдувания ветром и т. д. Процесс переноса тепла от поверхности твёрдого тела к движущейся жидкости или газу и наоборот называется конвективным теплообменом, т. е. теплоотдачей.
Тепловой поток в процессе теплоотдачи пропорционален разности температур стенки t c и жидкости (газа) t ж(г):
q = a(t c – t ж(г)). (4.13)
Выражение (4.13) называется законом Ньютона-Рихмана. Коэффициент пропорциональности a называется коэффициентом теплоотдачи; его размерность – Вт/(м2×K). Он характеризует интенсивность процесса теплоотдачи. Коэффициент a определяют экспериментально, измеряя количество переданной теплоты Q = q × F ×tи разность температур (t c – t ж(г)) в процессе теплоотдачи за время t от поверхности с известной площадью F. При выполнении теплотехнических расчётов, например теплопритоков в рефрижераторный вагон через его ограждения, величину a рассчитывают по специальным эмпирическим зависимостям, учитывающим физические свойства сред и конкретные условия теплообмена (прежде всего скорость омывания жидкостью (газом) твёрдой поверхности).
По природе движения жидкости (газа) различают естественную и вынужденную конвекции. Каждая из них обусловливается напором, побуждающим движение.
Естественная (свободная) конвекция возникает за счёт теплового расширения жидкости (газа) вблизи нагретой поверхности, например при печном или электрическом обогреве. Интенсивность свободной конвекции возрастает с увеличением разности температур (t c – t ж(г)) и температурного коэффициента объёмного расширения b t при:
 ,
,
где v – удельный объём.
Создающаяся при нагревании разность плотностей вызывает подъёмную силу, равную разности выталкивающей (архимедовой) силы и силы тяжести:
 ,
,
где g – ускорение свободного падения.
Около холодной стенки разность (t c – t ж(г)) отрицательна, и естественное движение становится опускным. Интенсивность естественной конвекции невелика.
Вынужденная конвекция создаётся внешним источником напора (насосом, вентилятором, ветром); значение напора может быть выбрано по соображениям необходимости, например, обеспечение отвода заданного количества теплоты. Скорость движения жидкости (газа), связанная с напором квадратичной зависимостью, велика в объёме потока и близка к нулю в пристенной области вследствие действия сил вязкости и эффекта прилипания. Область развитого (турбулентного) потока и твёрдая стенка разделены тонким пограничным слоем с ламинарным (низкоскоростным, плавным) режимом течения жидкости (газа). В ламинарном слое преимущественным механизмом переноса теплоты является теплопроводность. Переход от ламинарного течения к турбулентному происходит при некотором (критическом) значении скорости: безвихревое движение внезапно сменяется хаотическим.
Отмеченные обстоятельства непосредственно влияют на коэффициент теплоотдачи при вынужденной конвекции, который зависит и от многих других величин: a = f (l, r, w, c, p, n, l…). На основании теории подобия множество факторов (скорость w, плотность r, вязкость n, линейный размер l и др.) удаётся свести в малое число безразмерных комплексов – чисел (критериев) подобия:
Nu = f (Re, Pr),
где Nu – число Нуссельта, Nu = (a× l) / l; Re – число Рейнольдса, Re = wl / n; Pr – число Прандтля, Pr = (c ×r× n) / l.
В координатах Nu, Re, Pr построены компактные номограммы, позволяющие вычислять коэффициент теплоотдачи с учётом реальных условий омывания. Критериальный подход реализован и в случае естественной конвекции.
Лучистый теплообмен
В теплотехнических расчётах хладотранспорта лучистый теплообмен учитывается лишь при анализе теплопритоков через наружные ограждения вагонов. При попадании тепловых лучей на какое-либо тело энергия электромагнитных колебаний им поглощается, снова превращаясь во внутреннюю энергию с соответствующим возрастанием температуры. Процесс распространения света характеризуется длиной волны l и частотой колебаний f:
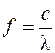 ,
,
где c – скорость света.
Суммарный удельный тепловой поток на всех длинах волн I, Вт/м2, определяется природой излучающего тела и его температурой. Он носит название собственного излучения.
Энергия падающего излучения частично поглощается, отражается или проникает сквозь тело. Относительные доли полного потока энергии носят название коэффициентов поглощения A, отражения R и пропускания D. Справедливо соотношение
A + R + D = 1.
Предельно возможные случаи таковы:
– абсолютно чёрное тело, A = 1;
–абсолютно белое тело, R = 1;
–абсолютно прозрачное тело, D = 1.
Совокупный процесс испускания, поглощения, отражения и пропускания энергии электромагнитных волн называется лучистым теплообменом. Его описание базируется на законе Стефана-Больцмана
I o = so× T 4,
где I o – плотность интегрального излучения абсолютно чёрного тела, Вт/м2; so – постоянная Стефана-Больцмана, Вт/(м2×К4); T – абсолютная температура, К.
Реальные (серые) тела излучают меньше:
I = e× I o,
где e – степень черноты, e = A < 1.
В системе двух тел плотность теплового потока взаимного (эффективного) облучения определяется зависимостью
 ,
,
гдеj1,2 – коэффициент облучённости (доля излучения первого тела, воспринимаемая вторым телом); eпр – приведённая степень черноты системы (формула (4.14)); с o– коэффициент излучения абсолютно чёрного тела, с o = so = 5,67 Вт/(м2×К4).
eпр = f (e1,e2 F 1, F 2) (4.14)
где F1, F2 – поверхности излучения тел первого и второго, м2.
Нагрев солнцем приводит к повышению температуры поверхности вагона на величину
 .
.
Здесь степень черноты вагона, e~0,7, а коэффициент теплоотдачи от наружной поверхности вагона к воздуху aн = 2.5. Дополнительный нагрев облучённой поверхности неподвижного вагона может достигать от 30 до 40 °С.
Теплопередача
Разделение теплопереноса на теплопроводность, конвекцию и излучение удобно для изучения каждого из этих процессов. В действительности же теплота передаётся двумя или даже тремя способами одновременно. В большинстве теплотехнических расчётов встречается ситуация передачи теплоты от одной жидкой (газообразной) среды к другой через разделяющую их стенку (рисунок 4.8), причём лучистый теплообмен учитывают только в коэффициенте теплоотдачи a1

Рисунок 4.8 – Температурное поле при передаче теплоты
из одной среды (1) в другую (2):
t 1 и t 2 – температуры первой и второй сред, разделённых плоской стенкой; t с1и t с2 – температуры на поверхностях стенки 1 и 2; d – толщина стенки; q – удельный тепловой поток через стенку
Поскольку у всех составляющих стационарного режима теплопереноса есть общая величина теплового потока Q, то для разности температур t 1 и t 2 можно записать очевидное соотношение
 .
.
Записывая это выражение относительно удельной плотности теплового потока, получим
q = k (t 1 – t 2),
где k – коэффициент теплопередачи, Вт/(м2×К).
Для случая плоской стенки F 1 = F 2 и тогда
 . (4.15)
. (4.15)
В знаменателе представлены все термические сопротивления на пути теплового потока. Величина k характеризует интенсивность процесса теплопередачи. Управление этим процессом осуществляют воздействием на все составляющие выражения (4.15).
Для интенсификации теплопередачи применяют оребрение (увеличение F), искусственную шероховатость поверхностей нагрева и усиление конвекции (увеличивают a); используют более теплопроводные материалы (снижают тепловое сопротивление R с) и т. д.
Для ослабления теплопритока усиливают тепловую изоляцию разделяющей стенки, влияя на её термическое сопротивление d/l, в том числе путём введения многослойной стенки.