Максимальное число входов мультиплексоров, выполненных в виде интегральных схем, равно восьми. Если требуется построить мультиплексорное устройство с большим числом входов, можно объединить мультиплексоры в схему так называемого дерева. Такое мультиплексорное дерево, построенное на четырехвходовых мультиплексорах, показано на рис. 6.29. Схема состоит из четырех мультиплексоров первого уровня с адресными переменными x1, х2 и мультиплексора второго уровня с адресными переменными x3, x4. Мультиплексорное устройство имеет 16 входов, разбитых на четверки, которые подключены к отдельным мультиплексорам первого уровня. Мультиплексор второго уровня, подключая к общему выходу устройства выходы отдельных мультиплексоров первого уровня, переключает четверки входов. Внутри же четверки требуемый вход выбирается мультиплексором первого уровня. По такой схеме, используя восьмивходовые мультиплексоры, можно построить мультиплексорное устройство, имеющее 64 входа.
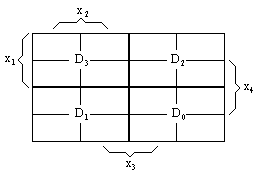
| Таблица 6.16 | Таблица 6.17 | |
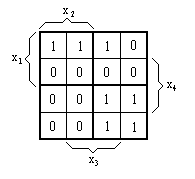
| 
|
В первом и втором уровнях мультиплексорного дерева можно использовать мультиплексоры с разным числом входов. Если в первом уровне такого дерева используются мультиплексоры с числом адресных переменных nадр1, а во втором - с числом переменных nадр2, то общее число входов мультиплексорного дерева будет равно nинф = 2nадр1 + nадр2, а число мультиплексоров в схеме составит 2nадр2 + 1.
Мультиплексорные деревья могут использоваться не только для переключения каналов, но и для синтеза логических функций.
Демультиплексоры.
Демультиплексор имеет один информационный вход и несколько выходов. Он представляет собой устройство, которое осуществляет коммутацию входа к одному из выходов, имеющему заданный адрес (номер). На рис. 6.30 показано символическое изображение демультиплексора с четырьмя выходами. Функционирование этого демультиплексора определяется табл. 6.18.
Объединяя мультиплексор с демультиплексором, можно построить устройство, в котором по заданным адресам один из входов подключается к одному из выходов (рис. 6.31). Таким образом, может быть выполнена любая комбинация соединений входов с выходами.
Например, при комбинации значений адресных переменных xl = l, x2 = 0, x3 = 0, x4 = 0 вход D2 окажется подключенным к выходу Y0.
Использование демультиплексора может существенно упростить построение логического устройства, имеющего несколько выходов, на которых формируются различные логические функции одних и тех же переменных.
Заметим, что если на вход демультиплексора подавать константу D = 1, то на выбранном в соответствии с заданным адресом выходе будет лог. 1, на остальных выходах - лог. 0. При этом по выполняемой функции демультиплексор превращается в дешифратор.
| Таблица 6.18 | |||||
| Адресные входы | Выходы | ||||
| A1 | A0 | Y0 | Y1 | Y2 | Y3 |
| D | |||||
| D | |||||
| D | |||||
| D |
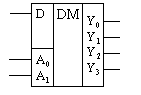
рис 6.30

рис 6.31
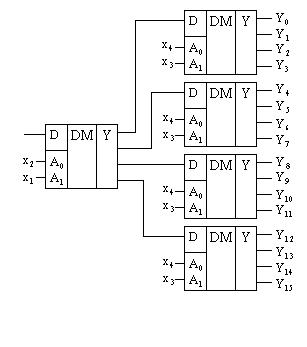
рис 6.32
При необходимости иметь большое число выходов может быть построено демультиплексорное дерево. На рис. 6.32 показано такое дерево, построенное на демультиплексорах с четырьмя выходами. Демультиплексор первого уровня подключает вход D к определенному демультиплексору второго уровня, демультиплексоры второго уровня выбирают нужный выход, куда и передается сигнал с входа D.
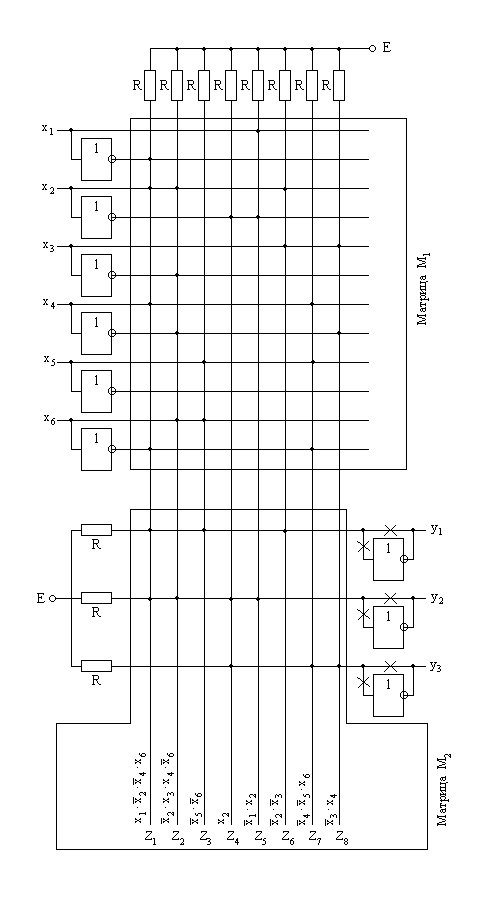
рис 6.33.