Пусть движение точки задано естественным способом. Вычислим скорость точки. Положение точки М на кривой можно описать радиус – вектором  , начало которого находится в центре О (рис. 3.7). Траектория определяет радиус-вектора, т.е радиус-вектор в данном случае является сложной функцией от времени, т.е.
, начало которого находится в центре О (рис. 3.7). Траектория определяет радиус-вектора, т.е радиус-вектор в данном случае является сложной функцией от времени, т.е.  .
.
Вычислим скорость точки М, имеем:
 (3.5)
(3.5)
Направление приращения радиус-вектора 
 в пределе
в пределе  совпадает с касательной осью
совпадает с касательной осью  в точке М (рис.3.7). Согласно определению производной
в точке М (рис.3.7). Согласно определению производной

где 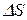 – приращение дуговой координаты. Вектор
– приращение дуговой координаты. Вектор  направлен в сторону возрастания дуговой координаты и совпадает с касательной к траектории в точке
направлен в сторону возрастания дуговой координаты и совпадает с касательной к траектории в точке 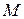 . Покажем, что этот вектор является единичным. Из рис. 3.7 видно, что
. Покажем, что этот вектор является единичным. Из рис. 3.7 видно, что

Скорость
 (3.6)
(3.6)
Величина  называется алгебраической скоростью точки. Знак производной определяет направление вектора скорости по
называется алгебраической скоростью точки. Знак производной определяет направление вектора скорости по  .
.
Ускорение точки при естественном способе задания движения
В соответствии с определением ускорения, имеем
 . (3.7)
. (3.7)
Вектор ускорения имеет два слагаемых. Первое слагаемое в выражении (3.7)– вектор  , направлен по
, направлен по  и определяет изменение модуля скорости. Второе слагаемое – вектор
и определяет изменение модуля скорости. Второе слагаемое – вектор  имеет направление вектора
имеет направление вектора 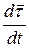 .
.
Покажем, что во втором слагаемом вектор 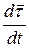 перпендикулярен вектору
перпендикулярен вектору  . Имеем: скалярный квадрат вектора
. Имеем: скалярный квадрат вектора  равен единице:
равен единице:
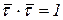 . (а)
. (а)
поэтому векторы  и
и  перпендикулярны друг другу (рис. 3.8).
перпендикулярны друг другу (рис. 3.8).
Справка
Скалярный квадрат  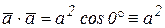 , если , если 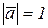 , то , то  .
Скалярное произведение .
Скалярное произведение   когда когда 
|
Дифференцируя по времени обе части тождества (а) получим:

 .
.
поэтому векторы  и
и  перпендикулярны друг другу (рис. 3.8).
перпендикулярны друг другу (рис. 3.8).
Направим единичный вектор  по вектору
по вектору 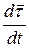 , тогда
, тогда
 . (3.8)
. (3.8)
По определению производной[1], имеем

Рис. 3.7
 . (3.9)
. (3.9)
Вектор  , как результат вычитания двух единичных векторов (
, как результат вычитания двух единичных векторов (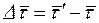 ), направлен на встречу вектора
), направлен на встречу вектора 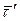 , т.е. направлен вовнутрь вогнутости траектории. Вычислим величину
, т.е. направлен вовнутрь вогнутости траектории. Вычислим величину  (рис. 3.8). Поскольку
(рис. 3.8). Поскольку  <<1, имеем
<<1, имеем

Подставляя полученный результат в (3.9) имеем
 . (3.10)
. (3.10)
При криволинейном движении точки угол смежности  зависит от
зависит от  , т.е. j =j (S(t)).
, т.е. j =j (S(t)).
Используя (3.8) и (3.10) и дифференцируя по времени j (S (t)) как сложную функцию, получим
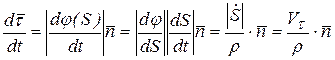 . (3.11)
. (3.11)
Здесь, 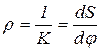 – радиус кривизны.
– радиус кривизны.
Вектор 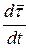 и совпадающий с ним по направлению единичный вектор
и совпадающий с ним по направлению единичный вектор  направлены параллельно предельному положению вектора
направлены параллельно предельному положению вектора  при
при  , т.е. векторы
, т.е. векторы  и
и  расположены в соприкасающейся плоскости
расположены в соприкасающейся плоскости
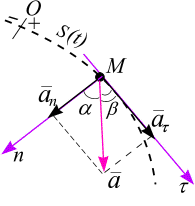
| кривой. Единичный вектор  перпендикулярен вектору перпендикулярен вектору  , направлен по главной нормали кривой в сторону ее вогнутости, так как в эту сторону направлено предельное положение вектора , направлен по главной нормали кривой в сторону ее вогнутости, так как в эту сторону направлено предельное положение вектора  (рис.3.8).
Итак, ускорение точки при естественном способе задания движения (3.7) запишем в виде (рис.3.8).
Итак, ускорение точки при естественном способе задания движения (3.7) запишем в виде
 или или 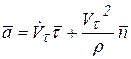 (3.12) (3.12)
|
| Рис. 3.9 |
Вектор ускорения точки М раскладывается на две векторные проекции по осям естественного трехгранника (рис.3.10). Проекция ускорения  на ось
на ось  называется касательным ускорением и обозначается
называется касательным ускорением и обозначается  :
:
 . (3.13)
. (3.13)
Проекция ускорения  на ось
на ось  называется нормальным ускорением и обозначается
называется нормальным ускорением и обозначается  :
:
 (3.14)
(3.14)
Таким образом,
 . (3.15)
. (3.15)
Учитывая ортогональность  и
и  , имеем (рис. 3.19):
, имеем (рис. 3.19):
 . (3.16)
. (3.16)
Касательное ускорение  характеризует изменение величины скорости, нормальное
характеризует изменение величины скорости, нормальное  – изменение направления вектора скорости.
– изменение направления вектора скорости.
Естественный способ задания движения –  + траектория + траектория
  , , 
 – касательное ускорение; – касательное ускорение;  - нормальное ускорение;. - нормальное ускорение;.
|