ЕСТЕСТВЕННЫЙ СПОСОБ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ
Содержание: естественный способ задания движения точки. Определения. Оси естественного трехгранника. Скорость и ускорение точки в проекциях на оси естественного трехгранника, касательное и нормальное ускорение точки.
Определения
 При естественном способе задания движения точки задается
При естественном способе задания движения точки задается
(рис. 3.1):
– траектория движения точки;
– начало и направление увеличения дуговой координаты;
– уравнение движения точки по траектории, как функция времени:  где S – дуговая координата, отчитываемая от начала движения.
где S – дуговая координата, отчитываемая от начала движения.
Для задания уравнения движения точки по траектории необходимо выбрать на заданной траектории точку О, принимаемую за начало отсчета дуговой координаты (рис. 3.1). Будем называть положительным то направление, которое соответствует возрастанию дуговой координаты. Обычно за  принимают момент времени, в который движущая точка проходит через выбранную точку О.
принимают момент времени, в который движущая точка проходит через выбранную точку О.
Движение точки может быть задано различными способами, например таблицей значений, графиком, одной или несколькими функциями.
Примером естественного способа задания движения является движение поезда: траектория и направление движения определены рельсами, а уравнение движения задано таблицей – расписанием движения поезда.
Рассмотрим движение точки, уравнение движения которой можно задать аналитически. Пусть шар падает вертикально вниз. В табл. 3.1 даны значения: время в секундах, расстояния в метрах. За нулевой момент времени выбираем момент начала падения шара. Через 1 с после начала падения шар пролетает 5м, через 2 с – 20 м, через 3 с – 45 м (табл. 3.1).
Табл. 3.1
Расписание движения падающего шара

| 1 | 2 | 3 | 4 | 5 | 6 | |
| S, м | 5 | 20 | 45 | 80 | 125 | 180 |
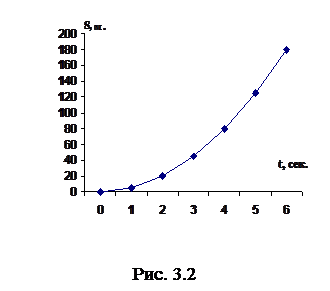 Нетрудно заметить, что путь, пройденный падающим шаром пропорционален квадрату времени: S(1)=5, S(2)=20=
Нетрудно заметить, что путь, пройденный падающим шаром пропорционален квадрату времени: S(1)=5, S(2)=20= 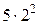 , S(3)= S(3)=
, S(3)= S(3)= 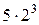 , и.т.д. Если отложить эти числа на графике в системе координат (
, и.т.д. Если отложить эти числа на графике в системе координат ( )
)
(рис. 3.2), то получим график зависимости пути, пройденному шаром от времени падения – графиком является парабола, которая описывается формулой 
Сравним два вида задания движения – координатный и естественный. Если движение точки задано координатным способом:  , то для перехода к естественному способу задания необходимо:
, то для перехода к естественному способу задания необходимо:
1. Составить и построить уравнение траектории – 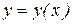 ;
;
2. Отметить положение точки в начальный момент времени и направление движения;
3. Составить уравнение движения точки по траектории, как функция времени:  .
.
Первые два пункта разобраны в предыдущей лекции. Покажем, как вычисляется уравнение движения точки, как функция дуговой координаты со временем - S(t).
Известно, что если точка движется в плоскости  , элемент дуги
, элемент дуги  связан с приращениями координат теоремой Пифагора, рис. 3.3:
связан с приращениями координат теоремой Пифагора, рис. 3.3:

При  , тогда
, тогда
Дифференциал дуги  связан с дифференциалами функций
связан с дифференциалами функций  и
и  (рис.3.3):
(рис.3.3):
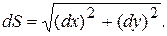 (3.1)
(3.1)
 Рис. 3.3 Рис. 3.3
| Интегрируя выражение (3.1), получим уравнение движения точки по криволинейной траектории, как функция времени:
 (3.2) (3.2)
|
Здесь  Если точка движется в одну сторону, дуговая координата
Если точка движется в одну сторону, дуговая координата 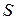 и путь
и путь  , пройденный точкой, совпадают. Если точка меняет направление движения, то путь
, пройденный точкой, совпадают. Если точка меняет направление движения, то путь 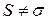 . Тогда путь
. Тогда путь  , пройденный точкой вычисляется по формуле (3.12), т.е.
, пройденный точкой вычисляется по формуле (3.12), т.е.

Справка.
Для расстановки пределов интегрирования в (3.3) нужно исследовать заданную функцию движения 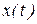 на экстремум, т.е. нужно определить знак первой производной от функции движения на экстремум, т.е. нужно определить знак первой производной от функции движения  для для  , при которых , при которых  . Тогда при . Тогда при  ,функция ,функция 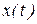 имеет экстремум, а точка меняет направление движения. имеет экстремум, а точка меняет направление движения.
|
Пример 3.1. Точка М движется прямолинейно, согласно уравнению
 (а)
(а)
Вычислить путь  , пройденный точкой М за 5с.
, пройденный точкой М за 5с.
Решение. Вычислим направление скорости точки. Имеем:


Вектор скорости  при
при  меняет направление, поэтому путь
меняет направление, поэтому путь  , пройденный точкой
, пройденный точкой  за 5с, будет вычисляться так:
за 5с, будет вычисляться так:

Точка за 5с. прошла 
Пример 3.3. Движение точки М задано уравнением:
 (м). (а)
(м). (а)
Вычислить путь  , пройденный точкой М за 10 с.
, пройденный точкой М за 10 с.
Решение. Вычислим направление скорости точки. Имеем:
 .
.
Вектор скорости  при
при  с меняет направление, поэтому путь
с меняет направление, поэтому путь 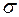 , пройденный точкой
, пройденный точкой  за 10 с, будет вычисляться так:
за 10 с, будет вычисляться так:


 (м).
(м).
Оси естественного трехгранника
 Рис. 3.4
Рис. 3.4
|
Пусть задана криволинейная траектории движущейся точки М, рис. 3.4. Если к движущейся точке «привязать» касательную, то вследствие «искривленности» кривой эта касательная с перемещением точки касания будет вращаться. Этим “кривая” отличается от “прямой”, для которой касательная сохраняет одно и то же направление для всех точек.
Пусть точка М за время  прошла путь по дуги, равный
прошла путь по дуги, равный  . Придав
. Придав 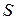 приращение
приращение  , получим другую точку
, получим другую точку  (рис. 3.4). Приращение угла наклона касательной при переходе от
(рис. 3.4). Приращение угла наклона касательной при переходе от  к
к  определяет угол
определяет угол 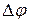 – угол между обеими касательными. Угол Dj будем называть углом смежности.
– угол между обеими касательными. Угол Dj будем называть углом смежности.
Определения
Принято кривизну кривой характеризовать углом поворота касательной, рассчитанным на единицу длины дуги.
Кривизной кривой К в точке М называют предел
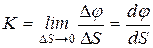 . (3.3)
. (3.3)
Замечание: для прямой –  ; для окружности –
; для окружности – 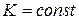 ; для различных точек на кривой, кривизна К различна.
; для различных точек на кривой, кривизна К различна.
Радиусом кривизны кривой r в точке М называют величину, обратную кривизне кривой в этой точке,
 (3.4)
(3.4)
Рассмотрим физический смысл радиуса кривизны. Во многих исследованиях представляется удобным приближенно заменить кривую вблизи рассматриваемой точки – окружностью, имеющей ту же кривизну, что и кривая в этой точке. Радиус этой окружности называется радиусом кривизны кривой в данной точке.
Вычислим радиус кривизны окружности (рис.3.5).

Рис. 3.5
Дуга окружности длиной S, опирающаяся на центральный угол j, связана с радиусом окружности зависимостью S=Rj.
Имеем 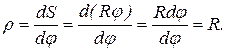
Для прямолинейной траектории угол Dj =0, тогда

|
Построение осей естественного трехгранника. Проведем к точке 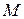 на дуге
на дуге  касательную ось
касательную ось  , рис. 3.6. Направим единичный вектор
, рис. 3.6. Направим единичный вектор  по направлению движения точки по оси
по направлению движения точки по оси  , направление которой определит положительное направление оси. Первой естественной осью является касательная Мτ. Проведем плоскость через две пересекающиеся прямые Mτ и М1τ1. Предельное положение этой плоскости при совпадении в пределе точки М1 с точкой М называется соприкасающейся плоскостью кривой в точке М (рис.3.6).
, направление которой определит положительное направление оси. Первой естественной осью является касательная Мτ. Проведем плоскость через две пересекающиеся прямые Mτ и М1τ1. Предельное положение этой плоскости при совпадении в пределе точки М1 с точкой М называется соприкасающейся плоскостью кривой в точке М (рис.3.6).

Рис. 3.6
Точка движется в соприкасающейся плоскости.
Перпендикулярно  и соприкасающейся плоскости располагается нормальная плоскость кривой. Линия пересечения нормальной плоскости и соприкасающейся плоскости называется осью главной нормали Мn. По главной нормали внутрь вогнутости кривой направим единичный вектор
и соприкасающейся плоскости располагается нормальная плоскость кривой. Линия пересечения нормальной плоскости и соприкасающейся плоскости называется осью главной нормали Мn. По главной нормали внутрь вогнутости кривой направим единичный вектор  . Он определяет положительное направление второй естественной оси – нормальной.
. Он определяет положительное направление второй естественной оси – нормальной.
Прямая, перпендикулярная главной нормали и касательной, называется бинормальной осью Мb. Единичный вектор  , направленный по бинормали так, чтобы три вектора образовывали правую систему осей координат, определит направление третьей естественной оси Мb. Плоскость, проходящая через
, направленный по бинормали так, чтобы три вектора образовывали правую систему осей координат, определит направление третьей естественной оси Мb. Плоскость, проходящая через 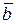 ,
,  , называется спрямляющей.
, называется спрямляющей.
Три взаимно перпендикулярные прямые Мτ, Мn, Мb, положительные направления которых совпадают с направлениями единичных векторов  ,
,  ,
, 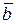 , образуют оси естественного трехгранника.
, образуют оси естественного трехгранника.