Определение и свойства двойного интеграла
 Пусть функция
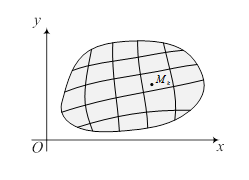
Пусть функция  определена в области (D) плоскости с заданной декартовой прямоугольной системой координат. Разобьем множество (D) на частичные подобласти (Dk),
определена в области (D) плоскости с заданной декартовой прямоугольной системой координат. Разобьем множество (D) на частичные подобласти (Dk),  ,
, 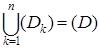 . Обозначим через dk диаметр множества (Dk):
. Обозначим через dk диаметр множества (Dk):  , через Δ Sk – площадь (Dk); число
, через Δ Sk – площадь (Dk); число 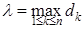 называется диаметром разбиения. В каждой подобласти (Dk) возьмем по точке
называется диаметром разбиения. В каждой подобласти (Dk) возьмем по точке  . Выражение
. Выражение
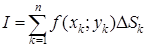
называется интегральной суммой функции  по области (D), отвечающей заданному разбиению и данному выбору точек. Если существует конечный предел интегральных сумм при
по области (D), отвечающей заданному разбиению и данному выбору точек. Если существует конечный предел интегральных сумм при 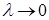 (предел, не зависящий ни от способа разбиения области (D), ни от выбора точек
(предел, не зависящий ни от способа разбиения области (D), ни от выбора точек  ), то этот предел называется двойным интегралом функции
), то этот предел называется двойным интегралом функции  по области (D) и обозначается
по области (D) и обозначается 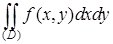 ; при этом говорят, что функция
; при этом говорят, что функция  интегрируема в области (или на множестве) (D).
интегрируема в области (или на множестве) (D).
Если функция определена и непрерывна в ограниченной замкнутой области (D), то она интегрируема в (D).
Двойной интеграл обладает свойствами линейности и аддитивности по области:

в последнем равенстве считается, что области (D 1) и (D 2) пересекаются по множеству нулевой площади (или вообще не пересекаются).
Сведение двойного интеграла к повторному
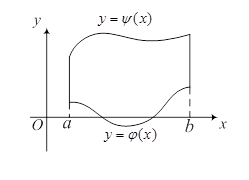 На практике вычисление двойного интеграла сводится к вычислению повторного. Если функция
На практике вычисление двойного интеграла сводится к вычислению повторного. Если функция 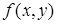 непрерывна в области (D), область (D) ограничена сверху линией
непрерывна в области (D), область (D) ограничена сверху линией 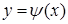 , снизу – линией
, снизу – линией 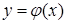 , слева – прямой
, слева – прямой  , справа – прямой
, справа – прямой 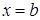 , то справедливо равенство
, то справедливо равенство
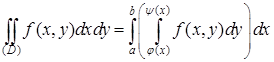 , (1)
, (1)
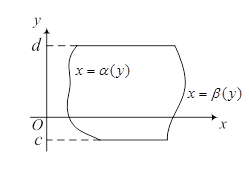 при этом сначала берется внутренний интеграл, который оказывается функцией от x, затем – внешний. Часто ради удобства повторный интеграл в равенстве (1) записывается в виде
при этом сначала берется внутренний интеграл, который оказывается функцией от x, затем – внешний. Часто ради удобства повторный интеграл в равенстве (1) записывается в виде
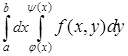 .
.
При переходе от двойного интеграла к повторному иногда удобнее внешнее интегрирование проводить по y, а внутреннее – по x:
 .
.
Пример 1. Вычислить повторный интеграл  .
.
 Решение. При интегрировании функции
Решение. При интегрировании функции  по y действуем так, как если бы переменное x являлось постоянной величиной:
по y действуем так, как если бы переменное x являлось постоянной величиной:
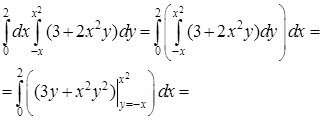
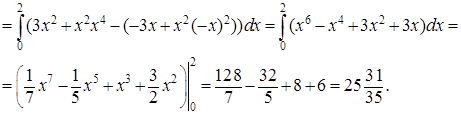
Область интегрирования изображена на рисунке.
Пример 2. Для повторного интеграла a) 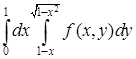 ; б)
; б)  построить область интегрирования.
построить область интегрирования.
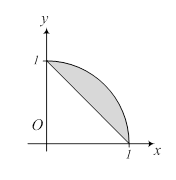 Решение. а) Область интегрирования (D) задается неравенствами
Решение. а) Область интегрирования (D) задается неравенствами

Поэтому область ограничена сверху полуокружностью 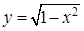 , снизу – прямой
, снизу – прямой 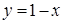 , и областью интегрирования является сегмент, изображенный на рисунке.
, и областью интегрирования является сегмент, изображенный на рисунке.
 б) Область интегрирования (D) задается неравенствами
б) Область интегрирования (D) задается неравенствами

Уравнение 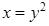 определяет параболу; уравнение
определяет параболу; уравнение 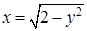 – правую полуокружность окружности
– правую полуокружность окружности 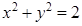 . Область, ограниченная этими линиями, показана на рисунке.
. Область, ограниченная этими линиями, показана на рисунке.
Пример 3. Записать двойной интеграл 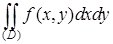 в виде повторного в различных порядках, если заданы границы области (D):
в виде повторного в различных порядках, если заданы границы области (D):
а) (D) – прямоугольник с вершинами в точках А (–2;1), В (3;1), С (3;4), D (–2;4);
б) (D): 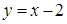 ,
, 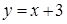 ,
,  ,
, 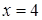 ;
;
в) (D):  ,
,  ,
, 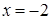 ,
, 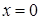 ;
;
г) (D):  ,
, 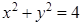
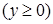 ;
;
 д) (D):
д) (D): 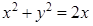 ,
, 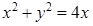 ,
, 
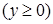 .
.
Решение. а) Построим область (D). Проекцией (D) на координатную ось Ох является отрезок [–2;3], и каждая прямая, проходящая через точку (х;0), 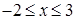 , параллельно оси Oy, пересекает область по отрезку, проекция которого на ось ординат одна и та же – [1;4]. Поэтому двойной интеграл запишется в виде повторного
, параллельно оси Oy, пересекает область по отрезку, проекция которого на ось ординат одна и та же – [1;4]. Поэтому двойной интеграл запишется в виде повторного
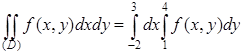 .
.
Аналогичными рассуждениями можно обосновать равенство
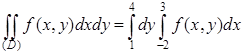 .
.
 б) Построим область (D). Сначала сведем двойной интеграл к повторному с внешним интегрированием по x. Проекцией области на координатную ось Ox является отрезок [1;4]. При каждом
б) Построим область (D). Сначала сведем двойной интеграл к повторному с внешним интегрированием по x. Проекцией области на координатную ось Ox является отрезок [1;4]. При каждом 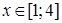 прямая, проходящая через точку (х;0) параллельно оси Oy, пересекает область (D) по отрезку, нижний конец которого имеет координаты
прямая, проходящая через точку (х;0) параллельно оси Oy, пересекает область (D) по отрезку, нижний конец которого имеет координаты 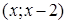 , верхний –
, верхний – 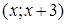 . Поэтому
. Поэтому
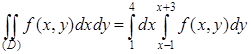 .
.
 Теперь сведем двойной интеграл к повторному, где внешнее интегрирование ведется по y, а внутреннее – по х. Проекцией области (D) на ось Oy является отрезок [–1;7]. Если зафиксировать
Теперь сведем двойной интеграл к повторному, где внешнее интегрирование ведется по y, а внутреннее – по х. Проекцией области (D) на ось Oy является отрезок [–1;7]. Если зафиксировать 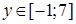 и через точку (0; y) провести прямую параллельно оси Ox, то пересечением этой прямой с областью будет отрезок, однако длина этого отрезка и его проекция на ось Ox будут зависеть от выбора
и через точку (0; y) провести прямую параллельно оси Ox, то пересечением этой прямой с областью будет отрезок, однако длина этого отрезка и его проекция на ось Ox будут зависеть от выбора 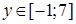 . Для решения задачи нам придется разбить область (D) на три части: (D 1), (D 2) и (D 3), как показано на рисунке. Тогда
. Для решения задачи нам придется разбить область (D) на три части: (D 1), (D 2) и (D 3), как показано на рисунке. Тогда
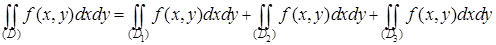 .
.
Проекцией (D 1) на Oy является отрезок [–1;2]. В уравнении прямой 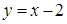 выразим х через y:
выразим х через y: 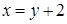 . Если взять
. Если взять 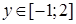 , то прямая, проходящая через точку (0; y) параллельно оси Ox, будет пересекать (D 1) по отрезку, проекцией которого на ось Ox является
, то прямая, проходящая через точку (0; y) параллельно оси Ox, будет пересекать (D 1) по отрезку, проекцией которого на ось Ox является  ; можно сказать, что, покуда y изменяется в пределах от (–1) до 2, x будет меняться от 1 до
; можно сказать, что, покуда y изменяется в пределах от (–1) до 2, x будет меняться от 1 до  . Поэтому
. Поэтому
 .
.
Область (D 2) является прямоугольником, поэтому
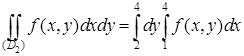 .
.
Проекцией (D 3) на ось Oy является отрезок [4;7]. Запишем уравнение прямой 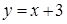 в виде
в виде 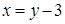 . Покуда y меняется в пределах от 4 до 7, переменное x меняется от
. Покуда y меняется в пределах от 4 до 7, переменное x меняется от  до 4 (проекцией на ось Ox пересечения прямой, проходящей через точку (0; y),
до 4 (проекцией на ось Ox пересечения прямой, проходящей через точку (0; y),  , с областью (D) является отрезок
, с областью (D) является отрезок  ). Поэтому
). Поэтому
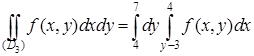 .
.
Таким образом,
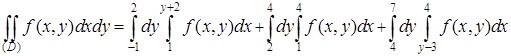 .
.
 в) Построим область (D). Возьмем сначала в качестве внешнего переменного x. Проекцией области (D) на ось Ox является отрезок [–2;0], и при каждом
в) Построим область (D). Возьмем сначала в качестве внешнего переменного x. Проекцией области (D) на ось Ox является отрезок [–2;0], и при каждом  соответствующая прямая (параллельная Oy и проходящая через точку (х;0)) пересечет область по отрезку, проекцией которого на ось Oy является
соответствующая прямая (параллельная Oy и проходящая через точку (х;0)) пересечет область по отрезку, проекцией которого на ось Oy является  . Таким образом,
. Таким образом,
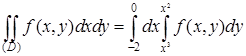 .
.
Изменим порядок интегрирования. Разобьем область (D) на две части: (D 1) и (D 2) (как на рисунке). Уравнения границы области запишем иначе: 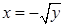 (так как
(так как 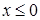 ),
),  . Проекцией (D 1) на Oy является отрезок [–8;0]; покуда y меняется от (–8) до 0, соответствующее x будет меняться от (–2) до
. Проекцией (D 1) на Oy является отрезок [–8;0]; покуда y меняется от (–8) до 0, соответствующее x будет меняться от (–2) до 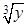 :
:
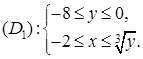
Поэтому
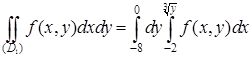 .
.
Аналогичным образом разбираемся с областью (D 2); покуда y меняется в пределах от 0 до 4, соответствующее x будет меняться от (–2) до 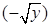 (иначе говоря, от абсциссы точки прямой
(иначе говоря, от абсциссы точки прямой 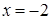 до абсциссы левой ветви параболы
до абсциссы левой ветви параболы  ):
):

Поэтому

и
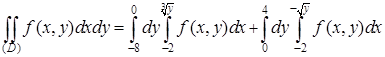 .
.
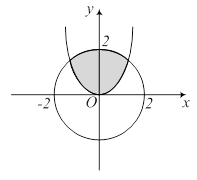 г) Построим область (D), ограниченную параболой
г) Построим область (D), ограниченную параболой  и окружностью
и окружностью 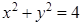 . Найдем точки пересечения этих линий, то есть решим систему уравнений
. Найдем точки пересечения этих линий, то есть решим систему уравнений

Решением системы являются точки 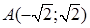 и
и  .
.
Сначала приведем двойной интеграл к повторному с внешним интегрированием по x. Проекцией области (D) на координатную ось Ox является отрезок 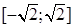 . Покуда х меняется в пределах от
. Покуда х меняется в пределах от 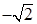 до
до  , соответствующее y будет меняться от
, соответствующее y будет меняться от  до
до  (говоря образно, от параболы до верхней полуокружности; если точнее, то – от ординаты соответствующей точки параболы до ординаты соответствующей точки верхней полуокружности). Поэтому
(говоря образно, от параболы до верхней полуокружности; если точнее, то – от ординаты соответствующей точки параболы до ординаты соответствующей точки верхней полуокружности). Поэтому
 .
.
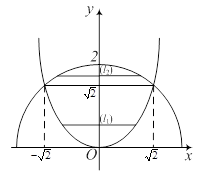 Перейдем к записи повторного интеграла с внешним интегрированием по y. В целом y меняется от 0 до 2, то есть проекцией области (D) на ось ординат является отрезок [0;2]. Однако аналитические выражения пределов изменения x зависят от того, какое y из отрезка [0;2] взято. Если y взято из отрезка
Перейдем к записи повторного интеграла с внешним интегрированием по y. В целом y меняется от 0 до 2, то есть проекцией области (D) на ось ординат является отрезок [0;2]. Однако аналитические выражения пределов изменения x зависят от того, какое y из отрезка [0;2] взято. Если y взято из отрезка 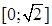 , то x будет меняться от абсциссы соответствующей точки левой ветви параболы
, то x будет меняться от абсциссы соответствующей точки левой ветви параболы  до абсциссы соответствующей точки правой ветви этой параболы (отрезок (l 1) на рисунке), то есть
до абсциссы соответствующей точки правой ветви этой параболы (отрезок (l 1) на рисунке), то есть 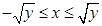 . Если же y меняется в пределах от
. Если же y меняется в пределах от  до 2, то x меняется от абсциссы соответствующей точки левой полуокружности до от абсциссы соответствующей точки правой полуокружности (отрезок (l 2) на рисунке), то есть
до 2, то x меняется от абсциссы соответствующей точки левой полуокружности до от абсциссы соответствующей точки правой полуокружности (отрезок (l 2) на рисунке), то есть 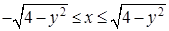 . Поэтому
. Поэтому
 .
.
д) Преобразуем уравнения линий, служащих границами (D):
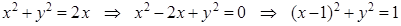
– окружность радиуса 1 с центром в точке (1;0);
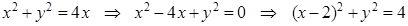
– окружность радиуса 2 с центром в точке (2;0).
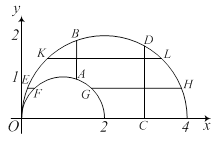 Областью (D) является множество, изображенное на рисунке; границей служит верхняя полуокружность
Областью (D) является множество, изображенное на рисунке; границей служит верхняя полуокружность 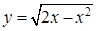 , верхняя полуокружность
, верхняя полуокружность 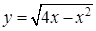 и отрезок прямой
и отрезок прямой  .
.
Сначала возьмем в качестве внешнего переменного х. Проекцией области (D) на ось Ox является отрезок [0;4]. Покуда х меняется в пределах от 0 до 2, y меняется от ординаты соответствующей точки полуокружности 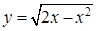 до ординаты соответствующей точки полуокружности
до ординаты соответствующей точки полуокружности 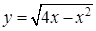 (соответствующая прямая пересекает область по отрезку AB). Если же х меняется в пределах от 2 до 4, то y меняется от 0 до ординаты соответствующей точки полуокружности
(соответствующая прямая пересекает область по отрезку AB). Если же х меняется в пределах от 2 до 4, то y меняется от 0 до ординаты соответствующей точки полуокружности 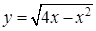 (соответствующая прямая пересекает область по отрезку CD). Таким образом,
(соответствующая прямая пересекает область по отрезку CD). Таким образом,
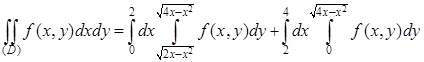 .
.
Возьмем теперь в качестве внешнего переменного y. Проекцией области (D) на ось Oy является отрезок [0;2]. Если взять y из отрезка [0;1) и через точку (0; y) провести прямую, параллельную Ox, то эта прямая пересечет область по двум отрезкам EF и GH, поэтому х будет меняться сначала от абсциссы соответствующей точки левой полуокружности большей окружности (точка Е) до абсциссы соответствующей точки левой полуокружности меньшей окружности (точка F), затем от абсциссы соответствующей точки правой полуокружности меньшей окружности (точка G) до абсциссы соответствующей точки правой полуокружности большей окружности (точка H). Если же y меняется от 1 до 2, то соответствующая прямая, параллельная оси Ox, будет пересекать область по отрезку KL, и х будет меняться от абсциссы соответствующей точки левой полуокружности большей окружности (точка K) до абсциссы соответствующей точки правой полуокружности той же окружности (точка L). Поэтому
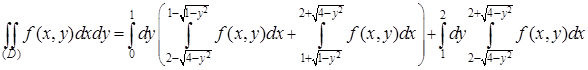 .
.
(Отметим, что если окружность задана уравнением 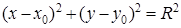 , то ее части задаются уравнениями:
, то ее части задаются уравнениями:
 – верхняя полуокружность,
– верхняя полуокружность,
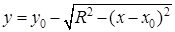 – нижняя полуокружность,
– нижняя полуокружность,
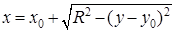 – правая полуокружность,
– правая полуокружность,
 – левая полуокружность.)
– левая полуокружность.)
Пример 4. Изменить порядок интегрирования в повторных интегралах:
а) 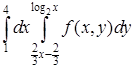 ; б)
; б) 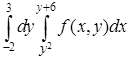 .
.
 Решение. а) Область интегрирования ограничена линиями
Решение. а) Область интегрирования ограничена линиями 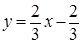 и
и  ,
, 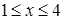 . Переменное y меняется от 0 до 2, и если через точку (0; y),
. Переменное y меняется от 0 до 2, и если через точку (0; y),  , провести прямую параллельно оси Ox, то прямая пересечет область по отрезку АВ, при этом х будет меняться от абсциссы точки А, то есть
, провести прямую параллельно оси Ox, то прямая пересечет область по отрезку АВ, при этом х будет меняться от абсциссы точки А, то есть  , до абсциссы точки В, то есть до
, до абсциссы точки В, то есть до  . Поэтому
. Поэтому
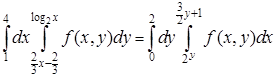 .
.
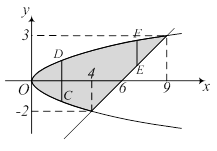 б) Построим область интегрирования, которая ограничена линиями
б) Построим область интегрирования, которая ограничена линиями 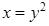 ,
, 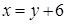 ,
, 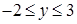 . Проекцией области на ось Ox является отрезок [0;9]. Точками пересечения параболы
. Проекцией области на ось Ox является отрезок [0;9]. Точками пересечения параболы 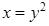 и прямой
и прямой 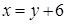 являются точки А (4;–2) и В (9;3). Если х меняется в пределах от 0 до 4, то соответствующая прямая, проходящая через точку (x;0) параллельно оси Oy, пересечет область по отрезку CD, то есть y будет меняться от ординаты точки нижней ветви параболы
являются точки А (4;–2) и В (9;3). Если х меняется в пределах от 0 до 4, то соответствующая прямая, проходящая через точку (x;0) параллельно оси Oy, пересечет область по отрезку CD, то есть y будет меняться от ординаты точки нижней ветви параболы  до ординаты точки верхней ветви параболы
до ординаты точки верхней ветви параболы 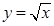 (отрезок CD). Если же х находится в пределах от 4 до 9, то y меняется в пределах от ординаты точки прямой (точка Е) до ординаты точки верхней ветви параболы (точка F). Поэтому
(отрезок CD). Если же х находится в пределах от 4 до 9, то y меняется в пределах от ординаты точки прямой (точка Е) до ординаты точки верхней ветви параболы (точка F). Поэтому
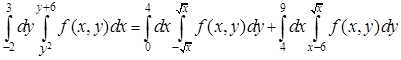 .
.