
| Вращением твердого тела вокруг неподвижной точки А в плоскостиназывается такое его движение, при котором точка А остаются неподвижной в течение всего времени движении тела, а все другие точки тела вращаются вокруг точки  в плоскости в плоскости  по окружности соответствующего радиуса (рис. 4.4). по окружности соответствующего радиуса (рис. 4.4).
|
| Рис. 4.4 |
Точка А называется центром вращения тела.
В этом случае тело имеет одну степень свободы и его уравнение движения имеет вид:
 . (4.2)
. (4.2)
Пусть при движении тела остаются неподвижными две точки принадлежащие телу (точки  на рис. 4.5). При этом неподвижными останутся все точки тела, расположенные на прямой, проходящей через эти неподвижные точки. Прямая
на рис. 4.5). При этом неподвижными останутся все точки тела, расположенные на прямой, проходящей через эти неподвижные точки. Прямая  называется осью вращения.
называется осью вращения.
Вращением твердого телавокруг неподвижной оси называется такое его движение, при котором точки тела, расположенные на оси, жестко связанной с телом, остаются неподвижными в течение всего времени движения.

| Через ось вращения проведем неподвижную плоскость П0 и подвижную П, скрепленную с вращающимся телом (рис. 4.5). Тогда в момент времени t положение подвижной плоскости и, следовательно, абсолютно твердого тела определяется углом между плоскостями –  . Угол . Угол  называется углом поворота тела. называется углом поворота тела.
|
| Рис. 4.5 |
Совместим декартову систему координат  с телом так, чтобы ось вращения тела
с телом так, чтобы ось вращения тела  совпала с осью
совпала с осью  , тогда плоскость
, тогда плоскость  будет перпендикулярна оси вращения.
будет перпендикулярна оси вращения.
Все точки, лежащие на прямой, параллельной оси вращения и отстоящей от нее на  , будут вращаться вместе с телом в плоскости
, будут вращаться вместе с телом в плоскости  по окружности, радиус которой равен
по окружности, радиус которой равен  (рис. 4.5). За полюс выберем точку А (отметим, что
(рис. 4.5). За полюс выберем точку А (отметим, что 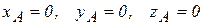 ). Проведем в плоскости
). Проведем в плоскости  прямую
прямую  . В рассматриваемом случае положение тела относительно выбранной системы отсчета полностью определяется в любой момент времени одним параметром
. В рассматриваемом случае положение тела относительно выбранной системы отсчета полностью определяется в любой момент времени одним параметром
 , (4.2’)
, (4.2’)
т.е. углом, который отрезок АВ образует с осью Aх.
Уравнение (4.1’) называют уравнением вращения твердого тела вокруг неподвижной оси. Угол  в правой декартовой системе координат считается положительным, если он откладывается против часовой стрелки, при этом смотреть нужно с положительного направления оси
в правой декартовой системе координат считается положительным, если он откладывается против часовой стрелки, при этом смотреть нужно с положительного направления оси  . Траектории всех точек тела при его вращении вокруг неподвижной оси являются окружности, расположенные в плоскостях, перпендикулярных оси вращения.
. Траектории всех точек тела при его вращении вокруг неподвижной оси являются окружности, расположенные в плоскостях, перпендикулярных оси вращения.
Угловая скорости и угловое ускорение тела. Введем единичный вектор оси вращения –  (рис. 4.6), направленный по оси вращения
(рис. 4.6), направленный по оси вращения  .
.
 Средней угловой скоростью
Средней угловой скоростью  тела, повернувшегося за время
тела, повернувшегося за время  на угол
на угол  называют соотношение
называют соотношение  , т.е.
, т.е.
 .
.
Мгновенная угловая скорость тела  в момент времени t определяется как предел средней угловой скорости при
в момент времени t определяется как предел средней угловой скорости при
Δt → 0, т.е.
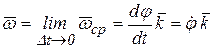

 (4.3)
(4.3)
Вектор угловой скорости  параллелен единичному вектору
параллелен единичному вектору  .
.
Модуль угловой скорости обозначается через  и равен
и равен
 (4.3’)
(4.3’)
Размерность угловой скорости [w]=угол/время=рад/с=с-1. В технике угловая скорость – это частота вращения, выраженная в оборотах в минуту. За 1 мин. тело повернется на угол 2pn, здесь n – число оборотов в минуту. Разделим этот угол на число секунд в минуту, получим
 ;
; 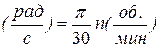 . (4.4)
. (4.4)
| Угловая скорость - это векторная величина, характеризующая быстроту и направление вращения тела |
Средним угловым ускорением тела  за время Δt называется отношение
за время Δt называется отношение  , т.е.
, т.е.
 .
.
Угловым ускорением твердого тела 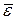 в момент времени t называют предел, к которому стремится среднее ускорение при Δt → 0, т.е.
в момент времени t называют предел, к которому стремится среднее ускорение при Δt → 0, т.е.
 .
. 
 (4.5)
(4.5)
Модуль углового ускорения обозначается через  и равен
и равен

 . (4.5’)
. (4.5’)
Размерность углового ускорения [e]=рад/с2=с-2.
| Угловое ускорение – это векторная величина, которая характеризует быстроту изменения модуля и направления вектора угловой скорости. |
Введем определения:
 – модуль угловой скорости тела,
– модуль угловой скорости тела,
 – модуль углового ускорения тела.
– модуль углового ускорения тела.
Знак производной  определяет направление вращения тела:
определяет направление вращения тела:
– при 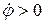 , тело вращается против часовой стрелки;
, тело вращается против часовой стрелки;
– при  , тело вращается по часовой стрелки;
, тело вращается по часовой стрелки;
– при  ,
, 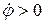 , или
, или 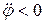 ,
,  – тело движется ускоренно;
– тело движется ускоренно;
– при  ,
,  или
или 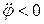 ,
,  – тело движется замедленно.
– тело движется замедленно.
Модуль угловой скорости  и модуль углового ускорения
и модуль углового ускорения  на рисунках изображают дуговыми стрелками вокруг оси вращения тела. Если первая и вторая производные от угла поворота имеют одинаковые знаки, т.е.
на рисунках изображают дуговыми стрелками вокруг оси вращения тела. Если первая и вторая производные от угла поворота имеют одинаковые знаки, т.е.  ,
,  (рис. 4.7, а), или
(рис. 4.7, а), или  ,
, 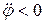 , то тело вращается ускоренно и дуговые стрелки направлены в одну сторону. Если первая и вторая производные от угла поворота имеют разные знаки, т.е.
, то тело вращается ускоренно и дуговые стрелки направлены в одну сторону. Если первая и вторая производные от угла поворота имеют разные знаки, т.е.  ,
, 
(рис. 4.7, б), или 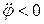 ,
,  , то тело вращается замедленно, тогда дуговые стрелки направлены в разные стороны.
, то тело вращается замедленно, тогда дуговые стрелки направлены в разные стороны.
| |||
| Рис. 4.7 |
Скорость и ускорение точек твердого тела при его вращении вокруг неподвижной оси. Все точки тела, отстоящие от оси вращения  на одном расстоянии, вращаются по одному радиусу
на одном расстоянии, вращаются по одному радиусу  (рис. 4.8, а). Точки, лежащие в плоскости, перпендикулярной оси вращения (в плоскостях
(рис. 4.8, а). Точки, лежащие в плоскости, перпендикулярной оси вращения (в плоскостях 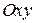 ), одновременно поворачиваются на один и тот же угол
), одновременно поворачиваются на один и тот же угол  (рис. 4.8, б).
(рис. 4.8, б).
 а
а
|
 б
б
|
| Рис. 4.8 |
Путь, который проходит точка тела  из положения
из положения  в положение М, по дуге S выражается через угол
в положение М, по дуге S выражается через угол  зависимостью
зависимостью  =
=  , где
, где  – радиус окружности по которой движется точка, рис. 4.7, б. Приведем оси естественного трехгранника к точке М. Ось
– радиус окружности по которой движется точка, рис. 4.7, б. Приведем оси естественного трехгранника к точке М. Ось  будет совпадать с радиусом и проходить через центр вращения А, ось
будет совпадать с радиусом и проходить через центр вращения А, ось  ей перпендикулярна и направлена по направлению вращения тела.
ей перпендикулярна и направлена по направлению вращения тела.
Точка  твердого тела при его вращении движется по окружности радиуса
твердого тела при его вращении движется по окружности радиуса  в направлении дуговой стрелки
в направлении дуговой стрелки  . Тогда, если
. Тогда, если  – уравнение вращения тела, то
– уравнение вращения тела, то 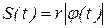 – уравнение движения точки тела М, заданной естественным способом.
– уравнение движения точки тела М, заданной естественным способом.
Тогда:
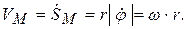 (4.6)
(4.6)
Здесь  - угловая скорость тела. Скорость точки М тела направлена по касательной к траектории –
- угловая скорость тела. Скорость точки М тела направлена по касательной к траектории –  (рис. 4.9, а).
(рис. 4.9, а).
 а а
| б

|
| Рис. 4.9 |
Ускорение точки М состоит из касательного и нормального ускорений (рис. 4.9, б):
 (4.7)
(4.7)
Направление касательного ускорения зависит от знака 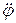 . При
. При 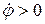 и
и  или
или  и
и  направления векторов
направления векторов  и
и 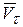 совпадают.
совпадают.
Если 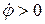 и
и  , то
, то  и
и 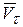 направлены противоположно друг другу. Полное ускорения точки М:
направлены противоположно друг другу. Полное ускорения точки М:
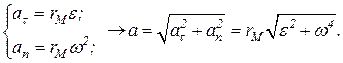
Обозначим через a – угол между полным ускорением и радиусом вращения точки, имеем
 .
.
Заметим, что нормальное ускорение всегда положительно. Угол a для всех точек тела один и тот же. Следовательно, если известен угол a, то в любой другой точке можно узнать направление ускорения, например в точке  . Откладывать его следует от вектора ускорения к радиусу вращения в направлении дуговой стрелки e независимо от направления вращения твердого тела (рис. 4.8, б).
. Откладывать его следует от вектора ускорения к радиусу вращения в направлении дуговой стрелки e независимо от направления вращения твердого тела (рис. 4.8, б).
