ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
2. Содержание. Основная теорема кинематики. Поступательное движение твердого тела. Теорема о траекториях, скоростях и ускорениях точек твердого тела при поступательном движении. Вращательное движение твердого тела вокруг неподвижной оси. Уравнение вращательного движения тела. Угол поворота, векторы угловой скорости и углового ускорения тела, модуль угловой скорости, модуль углового ускорения. Скорость и ускорение точек твердого тела при его вращении вокруг неподвижной оси. Преобразование простейших движений. Выражение скорости точки вращающегося тела и ее касательного и нормального ускорений в виде векторных произведений (уравнения Эйлера)[1]. Примеры.
Основная теорема кинематики (теорема Грасгофа)
Зависимость расстояний между точками абсолютно твердого тела (они неизменны при движении) приводит к зависимости между скоростями точек тела.
Теорема. При любом движении абсолютно твердого тела проекции скоростей точек на прямую, соединяющую эти точки, равны.
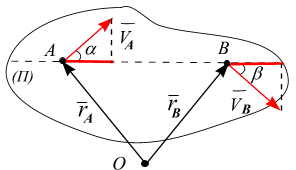 Рис. 4.1
Рис. 4.1
|
Рассмотрим абсолютно твердого тело  . Выберем на
. Выберем на  две точки А и В, расстояние между которыми равно
две точки А и В, расстояние между которыми равно 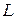 . Для доказательства теоремы используем зависимость радиус-векторов точек А и В (рис. 4.1)
. Для доказательства теоремы используем зависимость радиус-векторов точек А и В (рис. 4.1)
 .
.
Возведем обе части уравнения в скалярный квадрат. Имеем
 ,
,
где L=const. Дифференцируя по времени это выражение, получим:
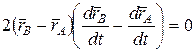 . (4.1)
. (4.1)
Заменив в этом выражении 
получим, имея в виду, что  :
:
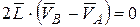
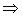
 .
.
Раскрывая скалярное произведение векторов в последнем равенстве, получаем:
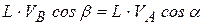
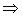
 .
.
Очевидно, что все точки тела, расположенные на прямой АВ, имеют одинаковые проекции скоростей на эту прямую.
Следствие. Проекции элементарных перемещений двух точек твердого тела на прямую, их соединяющую, равны.
Из (4.1), учитывая, что  получаем
получаем

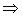 .
. 
из чего следует дифференциальная формула

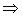 и
и  .
.
Доказанная теорема отражает основную особенность абсолютно твердого тела и может служить его определением. Зная скорости двух точек плоского абсолютно твердого тела и используя эту теорему, можно вычислить скорость любой его точки.
Рассмотрим простейшие виды движения абсолютно твердого тела. Такими простейшими движениями твердого тела являются поступательное движение тела и вращение тела вокруг неподвижной точки или оси, перпендикулярной плоскости тела и проходящей через точку вращения.
Поступательное движение твердого тела в плоскости
Поступательным движением твердого тела называют такое его движение, при котором любой отрезок, жестко связанный с этим телом, сохраняет неизменное направление при движении.
Из этого определения следует, что при поcтупательном движении абсолютно твердого тела в плоскости меняются при движении два параметра – координаты полюса  ,
,  , угол
, угол 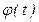 остается постоянным
остается постоянным
(рис. 4.2).
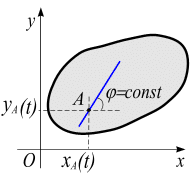 Рис. 4.2 Рис. 4.2
| Итак, уравнения поступательного движения в координатной форме имеют вид:
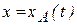 , ,  . (4.2)
Для описания поступательного движения тела достаточно знать движение его одной точки. Уравнения движения точки (4.2) будут уравнениями движения всего тела. . (4.2)
Для описания поступательного движения тела достаточно знать движение его одной точки. Уравнения движения точки (4.2) будут уравнениями движения всего тела.
|
Уравнения движения абсолютно твердого тела ни чем не отличаются от уравнений движения материальной точки: все точки тела имеют в каждый момент времени одинаковые перемещения, скорости и ускорения.
Теорема (о скоростях, ускорениях твердого тела при поступательном движении). При поступательном движении твердого тела траектории, скорости и ускорения всех точек тела одинаковы.
Выберем две точки А и В твердого тела, радиус– векторы этих точек удовлетворяют условию (рис. 4.3):
 , где
, где  .
.
Продифференцируем это уравнение:
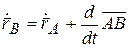

 .
.
Продифференцируем по времени последнее равенство:
 ,
, 
 .
.

Рис. 4.3.
При поступательном движении точки тела синхронно могут описывать какие угодно траектории – как прямолинейные, так и криволинейные.
Замечание. Понятия скорости и ускорения твердого тела имеют смысл только при его поступательном движении. Во всех других случаях движения речь идет о скорости и ускорении одной выбранной точки тела, например, о центре масс.