Численные методы. Практическое занятие № 1

 

Тема: «Интерполирование»

 

1. Вывести формулу для определения значений функции в любой точке отрезка 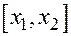, если между точками и проведена прямая линия.

Решение. Первый способ. Построим точки и на плоскости 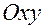(рис. 1).

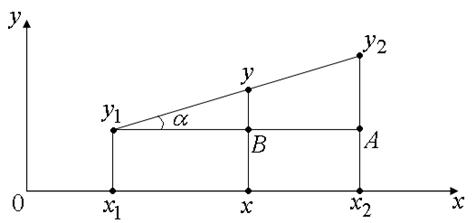
Рис. 1.

Из точки проведём прямую, параллельную оси и обозначим точку пересечения построенной прямой с прямой буквой . Пусть 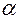- угол между прямым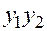и и 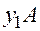. Вычислим тангенс угла 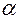. . 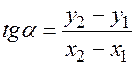Возьмём произвольную точку 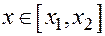и обозначим точку пересечения прямых и 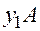буквой 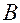. Так как треугольник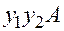и и подобны, то . Или в координатах . То есть 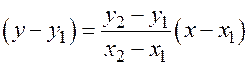. Оставляем неизвестное значение в левой части равенства . Вспоминая, что получаем окончательно

.

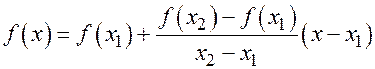Рассмотрим пример. Пусть 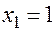, , 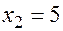, 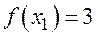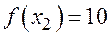. Тогда

.

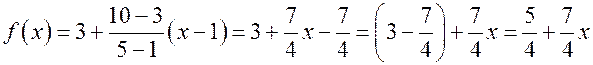Формула справедлива и для отрицательных углов .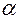

Пусть 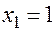, , 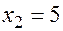, 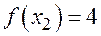. Тогда .

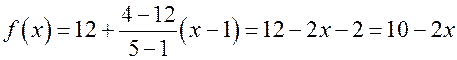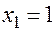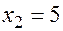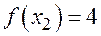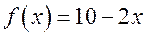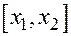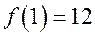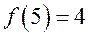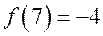Полученная формула справедлива и для нахождения точек экстраполяции. Если , , , , тогда . Вычислим, например, значение функции в точке , не принадлежащей отрезку . . Отметив точки , и на плоскости 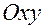легко проверить, что они лежат на одной прямой.

Второй способ. На лекции мы вывели интерполяционную формулу Ньютона, которая для двух точек и 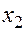будет иметь вид

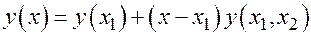, где 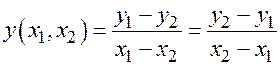. Откуда . Или

.

 

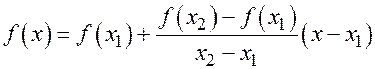2. Пусть и известны значения функции в точках 0, 1, 2, 3. Составить интерполяционный многочлен Ньютона для функции по указанным точкам 0, 1, 2, 3.

Решение. Составим таблицу разделённых разностей

 

 

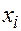
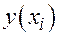
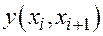
Составляем интерполяционный многочлен Ньютона по верхней косой строке

Подставляем значения подсчитанных разделённых разностей

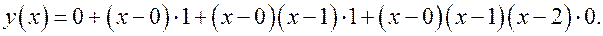
Раскрываем скобки

. То есть получили, что .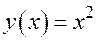

Таким образом, интерполяционный многочлен Ньютона в точности определил первоначально заданную функцию . Это связано с тем, что порядок точности интерполяции многочленом Ньютона равен количеству узлов интерполяции. В нашей задаче количество узлов равно 4, а степень многочлена, который мы пытались найти, равна 2. То есть порядок точности выше, чем степень искомого многочлена, поэтому многочлен Ньютона распознал искомую функцию точно.

Значит, по четырём точкам многочлен Ньютона может точно найти многочлен третьей степени, поскольку и в этом случае порядок точности будет выше, чем степень искомого многочлена. Давайте это проверим.

Задача 2.1. Пусть и известны значения функции в точках 0, 1, 2, 3. Составить интерполяционный многочлен Ньютона для функции по указанным точкам 0, 1, 2, 3.

Решение. Составим таблицу разделённых разностей

 

 

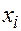
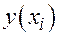
Составляем интерполяционный многочлен Ньютона по верхней косой строке

Подставляем значения подсчитанных разделённых разностей

Раскрываем скобки

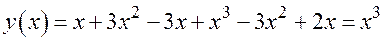. То есть получили, что , что мы и хотели получить. Таким образом, по узлам многочлен Ньютона

распознает полином степени .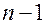

 

______________________________________________________________

 

3. Составить интерполяционный многочлен Ньютона для функции, заданной таблицей

х
у

 

Решение. Составим таблицу разделённых разностей

 

 

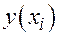
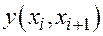
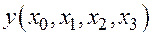
Видно, что четвёртая разделённая разность будет равна нулю, поэтому мы её не выписываем.

Составляем интерполяционный многочлен Ньютона по верхней косой строке

Подставляем значения подсчитанных разделённых разностей

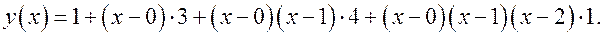
Раскрываем скобки

.

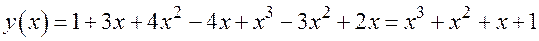Ответ. и для нахождения этого многочлена достаточно было взять 4 узла интерполяции.

 

 

Домашнее задание.

2. Построить для функции на отрезке интерполяционный многочлен Ньютона по точкам .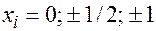

Ответ. .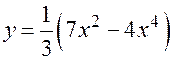

4. Составить интерполяционные формулы Ньютона и Лагранжа по следующей таблице

 

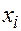
	-2	-1
	-5

 

Решение. Составим интерполяционный многочлен Ньютона. Заполняем таблицу разделённых разностей

 

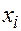
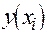
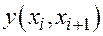
	-2	-5
	-1			-2

 

Составляем интерполяционный многочлен Ньютона по верхней косой строке

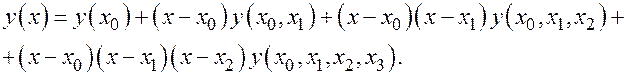
Подставляем значения подсчитанных разделённых разностей

 

Раскрываем скобки

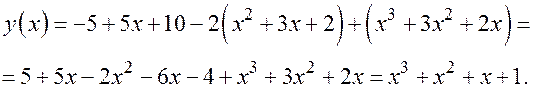
То есть получили, что интерполяционный многочлен Ньютона равен .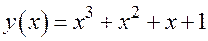

 

 

6. Для сеточной функции

 

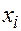
	-1
	-1

 

найти линейный и параболический многочлены Ньютона и на их основе подсчитать значение в точке . Оценить погрешность интерполяции.

Решение. Видно, что это протабулирована функция 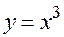. Но в условиях задачи речь идёт о линейном и параболическом многочленах Ньютона, поэтому здесь мы не получим многочлена третьей степени.

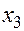Так как точка лежит ближе к узлу , то выбираем для квадратичной интерполяции узлы , а для линейной интерполяции узлы 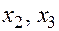. Составим таблицу разделённых разностей

 

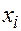
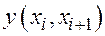
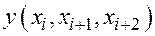
Строим .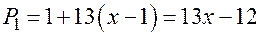

.

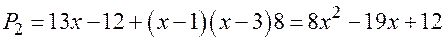Вычисляем .

.

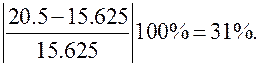а) Найдём относительные погрешности для и . Имеем для : Для :

То есть для многочлена относительная погрешность меньше в 4 раза.

b) Найдём априорную оценку погрешности для многочлена

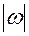. Максимум -вой производной определим численным дифференцированием. С этой целью продифференцируем дважды ; ; . Итак . Осталось найти . Так как от точки до точки расстояние равно 2, значит . Поэтому 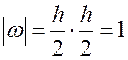. Подставляем 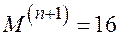и в формулу для априорной оценки точности 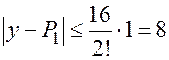. Таким образом, относительная априорная погрешность будет равна 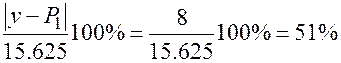. То есть относительная априорная погрешность почти в 2 раза превосходит относительную апостериорную погрешность.

Домашнее задание.

2. Построить для функции 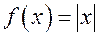на отрезке 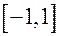интерполяционный многочлен Ньютона по точкам .

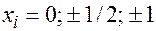Ответ. 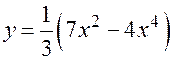.