Задача 119
Конструкция состоит из стержня ВС и АС, которые шарнирно соединены в точке С

Внешними связями, наложенными на конструкцию, являются жёсткая заделка в точке А и невесомый стержень в точке В. Конструкция находится в равновесии под действием сосредоточенной силы 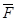 и распределённой нагрузки, действующей на половине участка BC по линейному закону с интенсивностью
и распределённой нагрузки, действующей на половине участка BC по линейному закону с интенсивностью  .
.
Определить реакции внешних и внутренних Связей в точках А, B и С если
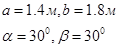
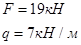
Для определения реакций связей расчленим конструкцию и рассмотрим равновесие каждой её части отдельно.
Рассмотрим равновесие стержня АС(рис 8).Проведём координатные оси xAy и изобразим действующие на стержень силы: силу  и реакции связей. Реакцию жёсткой заделки А изобразим моментом МА и двумя составляющими
и реакции связей. Реакцию жёсткой заделки А изобразим моментом МА и двумя составляющими  и
и  , реакцию шарнира С двумя её составляющими
, реакцию шарнира С двумя её составляющими  и
и 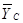 .
.

Стержень АС находится в равновесии под действием произвольной плоской системы сил, для которой можно записать три независимых уравнения равновесия.
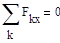
|

|

|

|

|

Рассмотрим равновесие стержня ВС. Проведём координатные оси xВy и изобразим действующие на стержень силы: равнодействующую распределённой нагрузки 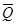 (
(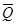 =qb) приложенную в точке К ВК=0,5b и реакции связей. Реакцию
=qb) приложенную в точке К ВК=0,5b и реакции связей. Реакцию  невесомого стержня в точке В направим горизонтально вправо, а реакции шарнира С (
невесомого стержня в точке В направим горизонтально вправо, а реакции шарнира С (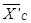 ,
,  ) направим, согласно аксиоме о равенстве сил действия и противодействия, в стороны противоположные реакциям шарнира С -
) направим, согласно аксиоме о равенстве сил действия и противодействия, в стороны противоположные реакциям шарнира С -  ,
,  стержня АС.
стержня АС.
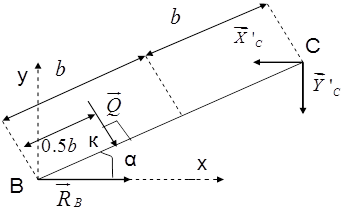
Рис. 9 Расчётная схема стержня ВС.
Стержень ВС находится в равновесии под действием произвольной плоской системы сил, для которой можно записать три независимых уравнения равновесия.
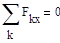
|
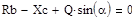
|

|

|

|

Число неизвестных величин с учётом аксиомы о равенстве сил действия и противодействия 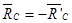 равно шести (реакции связей
равно шести (реакции связей 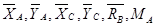 ). Число независимых уравнений равновесия для обеих частей конструкции тоже шесть. Задача является статически определимой.
). Число независимых уравнений равновесия для обеих частей конструкции тоже шесть. Задача является статически определимой.
Найдём значения внешних и внутренних реакций связей решив систему составленную из записанных ранее уравнений. Получим:
 -1,58кН
-1,58кН
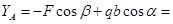 8,63кН
8,63кН
 15,512кН
15,512кН
 -11,88кН
-11,88кН
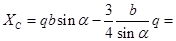 -7,92кН
-7,92кН
 =-6,85кН
=-6,85кН
Задача 219
Конструкция состоит из стержня ВС и АС, которые соединены невесомым стержнем С (рис.10)

Рис. 10
Внешними связями, наложенными на конструкцию, являются жёсткая заделка в точке А и неподвижная шарнирная опора в точке В. Конструкция находится в равновесии под действием пары сил с моментом М и сосредоточенной силы  . Исследовать влияние углов
. Исследовать влияние углов 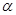 и
и  на реакции внутренних и внешних связей, а также найти оптимальные значения этих углов при которых значения реакций минимальны если:
на реакции внутренних и внешних связей, а также найти оптимальные значения этих углов при которых значения реакций минимальны если:
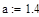
|
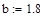
|
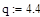
|

|

|

|

|

|
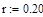
|
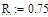
|
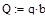
|
Для определения реакций связей расчленим конструкцию и рассмотрим равновесие каждой её части отдельно.
Рассмотрим равновесие стержня ВС(рис. 11). Проведём координатные оси xСy и изобразим действующие на стержень силы: пару сил с моментом М и реакции связей. Реакцию неподвижной шарнирной опоры В изображаем двумя её составляющими  , а реакцию
, а реакцию 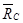 стержня С направим вертикально вверх.
стержня С направим вертикально вверх.
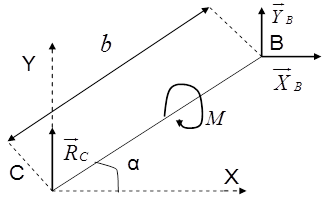
Рис.11 Расчётная схема стержня ВС.
Стержень ВС находится в равновесии под действием произвольной плоской системы сил, для которой можно записать три независимых уравнения равновесия.
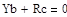
|
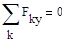
|

|
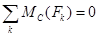
Рассмотрим равновесие стержня АС (рис.12).Проведём координатные оси xАy и изобразим действующие на стержень силы: сосредоточенную силу  и реакции связей. Реакцию жёсткой заделки А изобразим моментом МА и двумя составляющими
и реакции связей. Реакцию жёсткой заделки А изобразим моментом МА и двумя составляющими 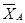 и
и 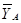 , а реакцию стержня С (
, а реакцию стержня С ( ) направим, согласно аксиоме о равенстве сил действия и противодействия, в сторону противоположную реакции стержня С -
) направим, согласно аксиоме о равенстве сил действия и противодействия, в сторону противоположную реакции стержня С -  стержня ВС.
стержня ВС.

Рис. 12 Расчётная схема стержня АС.

Стержень АС находится в равновесии под действием произвольной плоской системы сил, для которой можно записать три независимых уравнения равновесия.
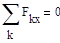
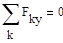

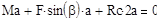
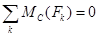
Число неизвестных величин с учётом аксиомы о равенстве сил действия и противодействия  равно шести (реакции связей
равно шести (реакции связей  ). Число независимых уравнений равновесия для обеих частей конструкции тоже шесть. Задача является статически определимой.
). Число независимых уравнений равновесия для обеих частей конструкции тоже шесть. Задача является статически определимой.


Как видно из полученных результатов: реакция 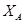 зависит только от угла
зависит только от угла  , реакции
, реакции  и
и  только от угла
только от угла 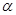 , а реакции
, а реакции  и
и  от
от  и
и 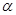 , реакция
, реакция  всегда равна 0.
всегда равна 0.
Задача 319
Конструкция состоит из двух стержней АС и BD соединенных шарнирно балкой CD (рис.13).

Рис.13 Схема конструкции.
Внешними связями, наложенными на конструкцию, являются жёсткая заделка в точке А и неподвижная шарнирная опора в точке В. Конструкция находится в равновесии под действием пары сил с моментом М, распределённой нагрузки, действующей на участке СD по линейному закону со средним значением 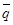 и распределённой нагрузки, действующей на участке АС по линейному закону, максимальное значение интенсивности которой
и распределённой нагрузки, действующей на участке АС по линейному закону, максимальное значение интенсивности которой 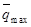 .
.
Определить  и
и 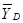 если:
если:
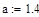
|

|

|

|

|
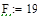
|
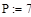
|

|
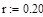
|

|

|
Для определения требуемых реакций расчленим конструкцию и рассмотрим равновесие каждой её части отдельно.
Рассмотрим равновесие стержня BD(рис.14).Проведём координатные оси xВy и изобразим действующие на стержень силы: пару сил с моментом М и реакции связей. Реакции неподвижной шарнирной опоры В и шарнира D изображаем двумя их составляющими  и
и 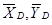 .
.

Рис. 14 Расчетная схема стержня BD
Стержень ВD находится в равновесии под действием произвольной плоской системы сил, для которой можно записать три независимых уравнения равновесия.
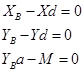
Рассмотрим равновесие балки СD(рис.15).Проведём координатные оси xСy и изобразим действующие на балку силы: равнодействующую распределённой нагрузки 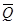 (
(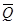 =qb) приложенную в точке К DК=0,5b и реакции связей. Реакцию шарнира С изображаем двумя её составляющими
=qb) приложенную в точке К DК=0,5b и реакции связей. Реакцию шарнира С изображаем двумя её составляющими 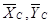 а реакции шарнира D (
а реакции шарнира D ( ,
,  ) направим, согласно аксиоме о равенстве сил действия и противодействия, в стороны противоположные реакциям шарнира D -
) направим, согласно аксиоме о равенстве сил действия и противодействия, в стороны противоположные реакциям шарнира D - 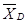 ,
, 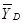 стержня BD.
стержня BD.

Рис.15 Расчётная схема балки CD.
Балка СD находится в равновесии под действием произвольной плоской системы сил, для которой можно записать три независимых уравнения равновесия.
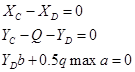
В данном случае для нахождения неизвестных реакций достаточно записать два следующих уравнения равновесия:
BD: 
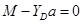
CD: 

Получили два уравнения с двумя неизвестными. Решая данную систему, находим:


Задача 419
Конструкция состоит из двух стержней АС и BС соединенных шарнирно в точке С (рис.16), а также двух блоков радиусов r и R находящихся на стержне AC на расстоянии 2b+a и а соответственно.
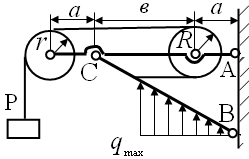
Рис.16 Схема конструкции.
Внешними связями, наложенными на конструкцию, являются неподвижные шарнирные опоры в точках А и В. Конструкция находится в равновесии под действием распределённой нагрузки, действующей на участке СK стержня CB по линейному закону, максимальное значение интенсивности которой  и груза весом P. Исследовать влияние угла
и груза весом P. Исследовать влияние угла 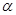 на реакции внутренних и внешних связей, а также найти оптимальные значения угла при котором значения реакций связей минимальны если:
на реакции внутренних и внешних связей, а также найти оптимальные значения угла при котором значения реакций связей минимальны если:

|
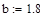
|

|
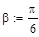
|
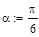
|

|

|

|

|
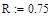
|

|
Для определения реакций связей расчленим конструкцию и рассмотрим равновесие каждой её части отдельно.
Рассмотрим равновесие стержня АС(рис. 17). Проведём координатные оси xАy и изобразим действующие на стержень силы: вес P, реакции нитей равные весу P и реакции связей. Реакцию неподвижной шарнирной опоры A и шарнира С изображаем двумя их составляющими 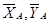 и
и 

Рис.17 Расчётная схема стержня АС.
Введём дополнительный угол:
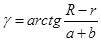
Стержень АС находится в равновесии под действием произвольной плоской системы сил, для которой можно записать три независимых уравнения равновесия.
 
|

|
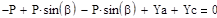
|
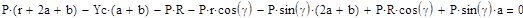
|
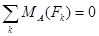
Рассмотрим равновесие стержня BС (рис.18).Проведём координатные оси xBy и изобразим действующие на стержень силы: реакцию нити равную весу P и приложенную в точке К, равнодействующую распределённой нагрузки 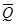 (
(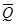 =0.5qmaxBK) приложенную в точке N BN=2/3*BK и реакции связей. Реакцию неподвижной шарнирной опоры B изображаем двумя её составляющими
=0.5qmaxBK) приложенную в точке N BN=2/3*BK и реакции связей. Реакцию неподвижной шарнирной опоры B изображаем двумя её составляющими 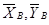 ,а реакцию шарнира С (
,а реакцию шарнира С ( ) направим, согласно аксиоме о равенстве сил действия и противодействия, в сторону противоположную реакции шарнира С -
) направим, согласно аксиоме о равенстве сил действия и противодействия, в сторону противоположную реакции шарнира С - 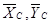 стержня АС.
стержня АС.

Рис.18 Расчётная схема стержня ВС.

Стержень BC находится в равновесии под действием произвольной плоской системы сил, для которой можно записать три независимых уравнения равновесия.
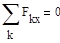 
|

|

|
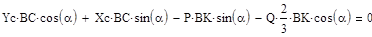
|
 Число неизвестных величин с учётом аксиомы о равенстве сил действия и противодействия
Число неизвестных величин с учётом аксиомы о равенстве сил действия и противодействия 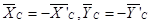 равно шести (реакции связей
равно шести (реакции связей  ). Число независимых уравнений равновесия для обеих частей конструкции тоже шесть. Задача является статически определимой.
). Число независимых уравнений равновесия для обеих частей конструкции тоже шесть. Задача является статически определимой.
Результаты расчетов
Решения систем линейных алгебраических уравнений и не сложно реализовать в пакете Mathcad, в котором для этого существует несколько способов [1, 10]. Так как кроме решения системы линейных алгебраических уравнений, требуется осуществить проверку их составления, воспользуемся возможностями символьных вычислений Mathcad. Численное решение полученных уравнений произведем с помощью блока решения  .
.
Список использованной литературы
1. Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах. Т.1 (Статика и кинематика) – М.: Наука, 1990;
2. Яблонский А.А., Никифорова В.М. Курс теоретической механики. Т.1 – М.: Высшая школа, 1984;
3. Бертяев В.Д. Теоретическая механика на базе Mathcad практикум – СПб.: БХВ – Петербург, 2005.
4. Кирьянов Д.В. Самоучитель Mathcad 12. - СПб.: БХВ – Петербург, 2004.