| № П/П | Разделы Дисциплины* | Код контролируемой компетенции (или ее части) Части) | Наименование оценочного средства |
| Линейная алгебра | ОПК-1 ОПК-2 ОПК-3 | Контрольная работа. Типовой расчет. Работа на практических занятиях: Текущий контроль Выполнения заданий | |
| Векторная алгебра | ОПК-1 ОПК-2 ОПК-3 | Контрольная работа. Типовой расчет. Работа на практических занятиях: Текущий контроль Выполнения заданий | |
| Аналитическая геометрия | ОПК-1 ОПК-2 ОПК-3 | Контрольная работа. Типовой расчет. Работа на практических занятиях: Текущий контроль Выполнения заданий | |
| Начало математического анализа | ОПК-1 ОПК-2 ОПК-3 | Контрольная работа. Типовой расчет. Работа на практических занятиях: Текущий контроль Выполнения заданий | |
| Вычисление пределов. непрерывность функций | ОПК-1 ОПК-2 ОПК-3 | Контрольная работа. Типовой расчет. Работа на практических занятиях: Текущий контроль Выполнения заданий | |
| Разделы 1-5 | ОПК-1 ОПК-2 ОПК-3 | Зачет. Экзамен | |
| Дифференциальное исчисление функций одной переменной. | ОПК-1 ОПК-2 ОПК-3 | Контрольная работа. Типовой расчет. Работа на практических занятиях: Текущий контроль Выполнения заданий | |
| Исследование функций и построение графиков. | ОПК-1 ОПК-2 ОПК-3 | Контрольная работа. Типовой расчет. Работа на практических занятиях: Текущий контроль Выполнения заданий | |
| Неопределённый интеграл | ОПК-1 ОПК-2 ОПК-3 | Контрольная работа. Типовой расчет. Работа на практических занятиях: Текущий контроль Выполнения заданий | |
| Определённый интеграл | ОПК-1 ОПК-2 ОПК-3 | Контрольная работа. Типовой расчет. Работа на практических занятиях: Текущий контроль Выполнения заданий | |
| Дифференциальное исчисление функций нескольких переменных | ОПК-1 ОПК-2 ОПК-3 | Контрольная работа. Типовой расчет. Работа на практических занятиях: Текущий контроль Выполнения заданий | |
| Разделы 7-11 | ОПК-1 ОПК-2 ОПК-3 | Экзамен | |
| Двойные и тройные интегралы | ОПК-1 ОПК-2 ОПК-3 | Контрольная работа. Типовой расчет. Работа на практических занятиях: Текущий контроль Выполнения заданий | |
| криволинейные и поверхностные интегралы | ОПК-1 ОПК-2 ОПК-3 | Контрольная работа. Типовой расчет. Работа на практических занятиях: Текущий контроль Выполнения заданий | |
| дифференциальные уравнения 1-го порядка | ОПК-1 ОПК-2 ОПК-3 | Контрольная работа. Типовой расчет. Работа на практических занятиях: Текущий контроль Выполнения заданий | |
| дифференциальные уравнения 2-го порядка | ОПК-1 ОПК-2 ОПК-3 | Контрольная работа. Типовой расчет. Работа на практических занятиях: Текущий контроль Выполнения заданий | |
| Числовые и степенные ряды. Ряды Фурье | ОПК-1 ОПК-2 ОПК-3 | Контрольная работа. Типовой расчет. Работа на практических занятиях: Текущий контроль Выполнения заданий | |
| Разделы 13-17 | ОПК-1 ОПК-2 ОПК-3 | Экзамен |
|
|
Описания элементов ФОС
Наименование: контрольная работа
Представление в ФОС: набор вариантов заданий
Варианты заданий:
Контрольная работа. (1 семестр) Линейная алгебра и векторная алгебра
1. Вычислить определитель: 
.
2. Найти обратную матрицу: 
.
3. Вычислить площадь параллелограмма, построенного на векторах а и в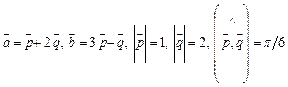 
.
4. Найти sin угла между векторами 
=(6,4,0) и 
=(1,-1,1).
|
|
5. Найти высоту тетраэдра с вершинами А(0,2,3), В(-2,4,0), С (7,0,3) и Д(4,3,1), опущенную из вершины Д.
6. Пусть А(0,-1,1), В(5,1,4), С (3,2,-1) и Д(4,1,3), найти ПрАД(3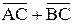 
)
7. Найти угол между 
и 
, если ^ , 
= 
=2, = и = + /3.
Контрольная работа. (2 семестр) Дифференцирование
1. Найти производные первого порядка от функций:
, 
, 
, 
.
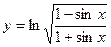2. Найти 
: 
.
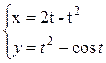3. Составить уравнение нормали к линии 
в точке ее пересечения с биссектрисой первого координатного угла.
4. Найти производную указанного порядка: 
, 
.
Контрольная работа. (3 семестр) Двойные, тройные интегралы
1. Найти объем тела ограниченного поверхностями: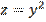 
, 
, 
, 
, 
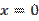2. Вычислить 
, если область Д ограничена прямыми x=2, y=x, x=2y.
3.Изменить порядок интегрирования
4. Вычислить двойной интеграл
; 
.
5. Найти площадь фигуры, ограниченной данными линиями
.
6.Пластинка D задана ограничивающими ее кривыми, m - поверхностная плотность. Найти массу пластинки:
; 
.
7. Найти объем тела, заданного ограничивающими его поверхностями:
y=16 
, y= , z=0, x+z=2.
8.Вычислить тройной интеграл
xdxdydz; V: y=10x, y=0, x=1, z=xy, z=0.
Критерии оценки:
Приведены в разделе 2
Наименование: типовой расчет
Представление в ФОС: набор вариантов заданий
Варианты заданий:
Типовой расчет. (1 семестр) Линейная алгебра и аналитическая геометрия
1. Найти произведение двух матриц.
2. Вычислить определитель, используя разложение по строке или столбцу.
3. Найти собственные значения матрицы 
, (решить уравнение 
относительно 
).
4. Вычислить обратную матрицу, если это возможно:
5. Проверить совместность системы уравнений, и, в случае совместности решить её: а) по формулам Крамера; б) с помощью обратной матрицы (матричным методом); в) методом Гаусса.
|
|
6. Вычислить работу силы 
на перемещении из точки 
в точку 
.
7. Даны вершины тетраэдра А(1;1,1), В(4;2;-1), С(-3;1;4), Д(2;6;0). Найдите объем тетраэдра и длину высоты опущенной из вершины Д.
8. Найдите проекцию точки 
на плоскость 
.
9. Найдите угол между двумя прямыми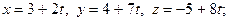 
10. Составить уравнение плоскости, проходящей через точку 
параллельно плоскости 
.
11.Дано каноническое уравнение эллипса 
Найдите большую и малую полуоси, фокальное расстояние, координаты вершин, фокусов, эксцентриситет, уравнения директрис и фокальные радиусы точки 
12. Дано каноническое уравнение параболы y 2 = 7 x. Найдите фокальный параметр параболы, координаты фокуса и уравнение директрисы.
13. Найдите каноническое уравнение эллипса и изобразите этот эллипс, его фокусы и директрисы, если известно, что малая полуось равна 3, уравнения директрис 
и 
Типовой расчет. (2 семестр) Интегралы
1. Найти неопределённый интеграл 
2. Вычислить определённый интеграл 
3. Найти неопределённый интеграл 
4. Вычислить определённый интеграл 
5. Найти неопределённый интеграл 
6. Вычислить определённый интеграл 
7. Вычислить определённый интеграл 
8. Вычислить определённый интеграл 
9. Вычислить определённый интеграл 
1. Вычислить площади фигур, ограниченных графиками функций
11. Вычислить площади фигур, ограниченных графиками функций
12. Вычислить площади фигур, ограниченных графиками функций в полярных координатах
13. Вычислить длину дуги 
14. Вычислить длину дуги 
15. Вычислить объём тела, ограниченного вращением графиков функции относительно оси Ox 
16.Определить работу (в джоулях), совершаемую при подъеме спутника Земли на высоту 
км. Масса спутника равна 
т, радиус Земли 
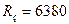км. Ускорение свободного падения 
у поверхности Земли положить равным 
.
т, 
км.
17. Вычислить приближенное значение определенного интеграла с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
Типовой расчет. (3 семестр) Дифференциальные уравнения.
1. Найти общий интеграл дифференциального уравнения. (Ответ представить в виде 
.)
2. Найти общий интеграл дифференциального уравнения.
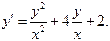
3. Найти общий интеграл дифференциального уравнения.
4. Найти решение задачи Коши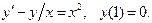 
5. Решить задачу Коши 
6. Найти решение задачи Коши 
7. Найти общий интеграл дифференциального уравнения 
8. Для данного дифференциального уравнения методом изоклин построить интегральную кривую, проходящую через точку 
.
9. Найти общее решение дифференциального уравнения 
10. Найти решение задачи Коши 
11. Найти общее решение дифференциального уравнения 
12. Найти общее решение дифференциального уравнения 
13. Найти общее решение дифференциального уравнения 
14. Найти общее решение дифференциального уравнения 
15. Найти решение задачи Коши 
Критерии оценки:
Приведены в разделе 2
Наименование: зачет
Представление в ФОС: перечень вопросов
Перечень вопросов для проведения зачета:
1.Свойства и графики основных элементарных функций.
2. Основные правила преобразования графиков. Сдвиги по осям координат. Симметрия относительно осей координат, начала координат.
3. Разложение многочлена на множители.
4.Решение алгебраических уравнений разложением на множители.
5. Деление многочлена на многочлен.
6. Решение алгебраических неравенств методом интервалов.
7.Решение показательных уравнений и неравенств.
8.Решение логарифмических уравнений и неравенств.
9. Решение простейших тригонометрических уравнений и неравенств. Запись общего решения.
10. Решение уравнений с модулем.
11. Решений неравенств с модулем.
12.Арифметическая и геометрическая прогрессии. Нахождение сумм п-членов прогрессии. Сумма бесконечно убывающей геометрической прогрессии.
Зачетный билет (примерный вариант)
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
"Ижевский государственный технический университет имени М.Т.Калашникова"
(ФГБОУ ВПО "ИжГТУ имени М.Т. Калашникова)
1. Представить рациональную дробь 
в виде суммы целой части и правильной дроби.
2. Аналитически и графически решить неравенство: 
.
3. Выразить 
через 
4. Дано уравнение 
. а) Решите уравнение; б) Укажите корни уравнения, принадлежащие отрезку 
.
5. Решить неравенство методом интервалов: 
.
6. Решить неравенство 
.
7. Решить неравенство 
8. Решить неравенство 
.
9. Построить график функции, выделяя полный квадрат и используя свойства преобразования графиков: 
.
10. Найти третий член бесконечно убывающей прогрессии, сумма которой равна 
, а второй ее член равен 
.
Критерии оценки:
Приведены в разделе 2
Наименование: экзамен
Представление в ФОС: перечень вопросов
Перечень вопросов для проведения экзамена:
Вопросы для подготовки к экзамену (1 семестр)
1. Матрицы. Действия над матрицами. Элементарные преобразования матриц.
2. Определители. Действия над определителями. Применение определителей.
3. Невырожденные матрицы. Обратная матрица. Ранг матрицы.
4. Системы линейных алгебраических уравнений (СЛАУ). Решение СЛАУ. Теорема Кронекера-Капелли.
5. Решение невырожденных СЛАУ. Формулы Крамера.
6. Решение СЛАУ методом Гаусса.
7. Системы линейных однородных алгебраических уравнений.
8. Векторы. Линейные операции над векторами. Проекция вектора на ось. Разложение вектора по ортам координатных осей. Действия над векторами, заданными проекциями.
9. Скалярное произведение векторов. Приложение скалярного произведения векторов.
10. Векторное произведение векторов. Приложение векторного произведения векторов.
11. Прямоугольная система координат. Применение прямоугольной системы координат. Преобразование системы координат.
12. Линии на плоскости. Уравнение прямой.
13. Основные задачи с использованием прямой линии на плоскости: угол между прямыми, расстояние от точки до прямой.
14. Линии второго порядка на плоскости. Эллипс. Парабола. Гипербола. Общее уравнение линий второго порядка на плоскости.
15. Поверхность и ее уравнение в пространстве. Уравнение линии в пространстве. Уравнение плоскости в пространстве. Основные задачи.
16. Уравнение прямой в пространстве. Основные задачи.
17. Множества. Числовые множества. Множество действительных чисел. Числовые промежутки. Окрестность точки.
18. Понятие функции. Числовые функции. График функции. Способы задания функции.
19. Основные характеристики функции. Обратная функция. Сложная функция.
20. Числовая последовательность. Предел числовой последовательности.
21. Предел функции в точке. Односторонние пределы.
22. Предел функции при x ® ¥. Бесконечно большая функция.
23. Бесконечно малые функции. Связь между функцией, ее пределом и бесконечно малой функцией. Связь между бесконечно большими и бесконечно малыми функциями.
24. Основные теоремы о пределах. Признаки существования пределов.
25. Первый и второй замечательные пределы.
26. Сравнение бесконечно малых функций. Эквивалентные бесконечно малые функции. Применение бесконечно малых функций.
27. Непрерывность функции. Точки разрыва функции и их классификация.
Вопросы для подготовки к экзамену (2 семестр)
1. Производная функции. Определение, примеры.
2. Дифференцируемость функции в точке. Дифференциал. Связь между дифференцируемостью и непрерывностью функции в точке.
3. Геометрический смысл производной и дифференциала функции в точке. Уравнение касательной и нормали.
4. Правила дифференцирования функций, связанные с арифметическими операциями.
5. Производная и дифференциал сложной функции. Свойство инвариантности формы дифференциала.
6. Обратная функция. Производная обратной функции.
7. Производные и дифференциалы высших порядков. Формула Лейбница.
8. Дифференцирование функций, заданных параметрически.
9. Теорема Роля.
10. Теорема Лагранжа.
11. Теорема Коши.
12. Правило Лопиталя.
13. Формула Тейлора.
14. Исследование функции на монотонность.
15. Экстремум функции. Необходимые и достаточные условия экстремума.
16. Выпуклость функции. Точки перегиба.
17. Асимптоты.
18. Первообразная функция, ее свойства.
19. Интегрирование по частям в неопределенном интеграле.
20. Замена переменной в неопределенном интеграле.
21. Интегрирование некоторых функций, содержащих квадратный трехчлен.
22. Интегрирование дробно-рациональных функций.
23. Интегрирование некоторых иррациональных функций.
24. Интегрирование тригонометрических функций.
25. Задачи, приводящие к понятию определенного интеграла.
26. Интегральная сумма. Определение определенного интеграла. Теорема существования определенного интеграла.
27. Свойства определенного интеграла.
28. Интегрирование по частям и замена переменной в определенном интеграле.
29. Несобственные интегралы 1-ого рода. Определение. Вычисление. Простой признак сравнения
30. Несобственные интегралы 1-ого рода. Предельный признак сравнения.
31. Несобственные интегралы 2-ого рода.
32. Применение определенного интеграла к вычислению площадей плоских фигур.
33. Применение определенного интеграла к вычислению длины дуги.
34. Применение определенного интеграла к вычислению объема тела по площадям параллельных сечений, объема тела вращения.
35. Окрестность точки. Замкнутые и открытые множества. Области
36. Способы задания ФНП. Линии уровня.
37. Предел и непрерывность ФНП.
38. Частные производные ФНП.
39. Дифференцируемость ФНП, дифференциал ФНП.
40. Производная по направлению, ее свойства.
41. Градиент, его свойства.
42. Геометрические приложения градиента: касательная плоскость и нормаль к поверхности.
43. Дифференциал сложной функции нескольких переменных.
44. Производные и дифференциалы высших порядков.
45. Дифференцирование неявно заданных функций.
46. Необходимые условия экстремума функции двух переменных. Экстремумы
47. Достаточные условия экстремума функции двух переменных.
48. Формула Тейлора для ФНП.
49. Достаточные условия экстремума ФНП, выраженные через второй дифференциал.
Вопросы для подготовки к экзамену (3 семестр)
1. Определение двойного и тройного интегралов. Их геометрический и физический смысл.
2. Основные свойства двойных и тройных интегралов.
3. Вычисление двойных интегралов двумя последовательными интегрированиями (случай прямоугольной области).
4.. Вычисление двойных интегралов двумя последовательными интегрированиями (общий случай).
5. Замена переменных в двойном интеграле.
6. Якобиан, его геометрический смысл.
7. Двойной интеграл в полярных координатах.
8. Тройной интеграл в цилиндрических координатах.
9. Тройной интеграл в сферических координатах.
10. Криволинейные интегралы.
11. Поверхностные интегралы.
12. Частные и общие решения дифференциального уравнения 1-го порядка.
13. Дифференциальные уравнения с разделяющимися переменными.
14. Однородные уравнения.
15. Линейные уравнения.
16. Уравнения Бернулли.
17. Частные и общие решения дифференциального уравнения 2-го порядка.
18. Вид общего решения линейного дифференциального уравнения второго порядка в случае, если корни характеристического уравнения действительные и различные.
19. Вид общего решения линейного однородного дифференциального уравнения 2-го порядка, если корни характеристического уравнения кратные.
20. Вид общего решения линейного однородного дифференциального уравнения 2-го порядка, если корни характеристического уравнения комплексные.
21. Теорема об общем решении линейного неоднородного дифференциального уравнения 2-го порядка.
22. Метод Лагранжа решения неоднородного линейного дифференциального уравнения 2-го порядка.
23. Числовые ряды.
24. Сходимость числовых рядов.
25. Признаки сходимости рядов с положительными членами.
26. Знакопеременные ряды. Действия над рядами.
27. Степенные ряды, радиус сходимости, область сходимости.
28. Ряды Фурье. Основные понятия
Экзаменационные билеты (примерный вариант)
ИЖЕВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ИМЕНИ М.Т. КАЛАШНИКОВА
КАФЕДРА ВЫСШЕЙ МАТЕМАТИКИ.
Математика (1 семестр). Экзаменационный билет № 1
1. (теория) Определители и методы их вычисления. Свойства определителей.
2. Найти момент силы 
, приложенной в точке В (3, -1, 5) относительно точки
А (4, -2, 3), а также модуль и направляющие косинусы вектора силы 
.
3. Проверить, являются ли точки А (3;-1;2), В (1;2;-1), С (-1;1;-3), Д (3;-5;3) вершинами трапеции.
4. Вычислить пределы 
; 
.
5. Написать уравнение диаметра окружности 
параллельного прямой
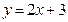. Сделать чертеж.
6. Решить систему уравнений матричным методом:
ИЖЕВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ИМЕНИ М.Т. КАЛАШНИКОВА
КАФЕДРА ВЫСШЕЙ МАТЕМАТИКИ.
МАТЕМАТИКА (2 СЕМЕСТР). ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 1
1. (теория) Исследование функций и построение графиков.
2.Понятие первообразной и неопределенного интеграла. Свойства и таблица интегралов.
3. Найти производную функции 
.
4. Исследовать функцию и построить ее график: 
.
5. Вычислить 
.
6. Вычислить 
.
7. Найти dz; 
: 
, если 
.
8. Найти наибольшее и наименьшее значение функции z = x2 +y2 – 4xy – 4 в квадрате: 0 ≤ x ≤ 4; 0 ≤ y ≤ 4.
ИЖЕВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ИМЕНИ М.Т. КАЛАШНИКОВА
КАФЕДРА ВЫСШЕЙ МАТЕМАТИКИ.
МАТЕМАТИКА (3 СЕМЕСТР). ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 1
1. Найти общее решение дифференциального уравнения 
и частное решение при условии 
.
2. Решить однородное дифференциальное уравнение 
.
3. Решить дифференциальное уравнение II-го порядка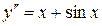 
.
4. Исследовать сходимость ряда с помощью признака Даламбера:
.
5. Вычислить какое число членов ряда надо взять, чтобы получить его сумму с точностью до 0,01: 
.
6. Найти интервал сходимости степенного ряда 
7.(теория) Дифференциальные уравнения 1-го порядка. Общее и частное решения. Задача Коши. Теорема существования и единственности решения. Дифференциальные уравнения с разделяющимися переменными и приводящиеся к ним.
Критерии оценки:
Приведены в разделе 2
Наименование: работа на практических занятиях: текущий контроль выполнения заданий
Представление в ФОС: перечень заданий
Варианты заданий: