Проведём исследование графика уравнения (4.7) методом сечения плоскостями.
Рассмотрим линии  , полученные в сечениях гиперболического параболоида плоскостями Y=h. Эти линии определяются системой уравнений:
, полученные в сечениях гиперболического параболоида плоскостями Y=h. Эти линии определяются системой уравнений:
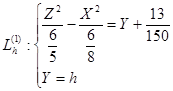
Следовательно, уравнения проекций линий  на плоскость ZO'X имеют вид:
на плоскость ZO'X имеют вид:
 :
: 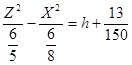
Рассмотрим три случая:
Если h + 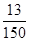 >0, h >
>0, h > 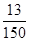 , запишем полученное уравнение в виде:
, запишем полученное уравнение в виде:
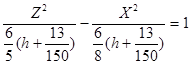 (4.8)
(4.8)
Уравнение (4.8) задаёт гиперболы с центрами в точках (0, h,0).
Полуоси гипербол:
a = 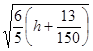 - действительная полуось, b =
- действительная полуось, b = 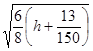 - мнимая полуось, увеличиваются с увеличением h. При различных значениях h получим семейство соответствующих гипербол:
- мнимая полуось, увеличиваются с увеличением h. При различных значениях h получим семейство соответствующих гипербол:
h = 1 a= 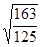 ; b=
; b= 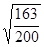 ;
; 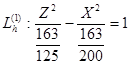
h=2 a=  ; b=
; b=  ;
; 
h=3 a=  ; b=
; b=  ;
; 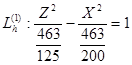
Изобразим данные гиперболы на рисунке:

Если h + 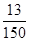 =0, h =
=0, h = 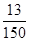 , запишем полученное уравнение в виде:
, запишем полученное уравнение в виде:
 или
или 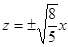
Данное уравнение задаёт две пересекающиеся прямые. Изобразим их на рисунке:
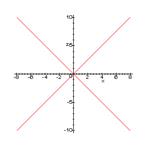
Если h + 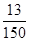 < 0, h<
< 0, h< 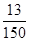 , запишем полученное уравнение в виде:
, запишем полученное уравнение в виде:
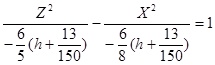
Данное уравнение задаёт сопряжённые гиперболы с центрами в точке (0, h, 0).
Полуоси гипербол:
a= 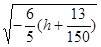 - действительная полуось, b=
- действительная полуось, b= 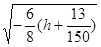 - мнимая полуось, увеличиваются с увеличением | h |.
- мнимая полуось, увеличиваются с увеличением | h |.
При различных значениях h получаем семейство соответствующих гипербол:
h=-1 a=  ; b=
; b= 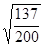 ;
; 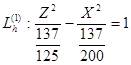
h=-2 a= 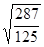 ; b=
; b=  ;
; 
h=-3 a=  ; b=
; b= 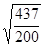 ;
; 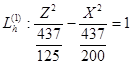
Изобразим данные гиперболы на рисунке:
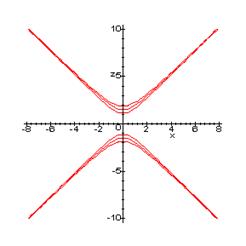
Рассмотрим линии 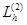 , полученные в сечениях гиперболического параболоида плоскостями Z=h. Эти линии определяются системой уравнений:
, полученные в сечениях гиперболического параболоида плоскостями Z=h. Эти линии определяются системой уравнений:

Следовательно, уравнения проекций линий 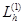 на плоскость XO'Y имеют вид:
на плоскость XO'Y имеют вид:
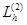 :
:  (4.9)
(4.9)
Уравнение (4.9) задаёт параболы, с вершинами в точках V(0, 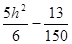 , h) и параметром
, h) и параметром
p= 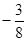 . При различных h получим семейство соответствующих парабол:
. При различных h получим семейство соответствующих парабол:
h = ±1 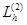 :
: 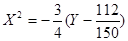
h = ±2 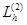 :
: 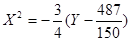
h = ±3 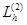 :
: 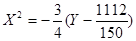
Изобразим данные параболы на рисунке:

Рассмотрим линии 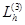 , полученные в сечениях гиперболического параболоида плоскостями X=h. Эти линии определяются системой уравнений:
, полученные в сечениях гиперболического параболоида плоскостями X=h. Эти линии определяются системой уравнений:
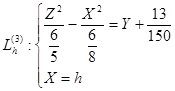
Следовательно, уравнения проекций линий 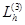 на плоскость YO'Z имеют вид:
на плоскость YO'Z имеют вид:
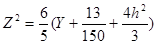 (4.10)
(4.10)
Уравнение (4.10) задаёт параболы, с вершинами в V(h, 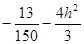 ,0) и параметром p=
,0) и параметром p= 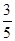 . При различных h получаем семейство соответствующих парабол.
. При различных h получаем семейство соответствующих парабол.
h = ±1 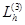 :
: 
h = ±2 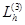 :
: 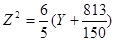
h = ±3 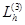 :
: 
Изобразим данные параболы на рисунке:
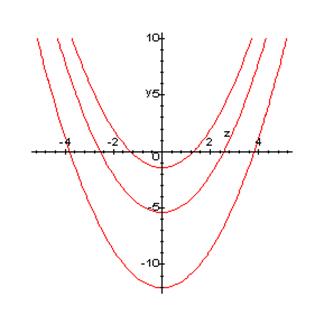
Графики уравнения поверхности
Изобразим поверхность второго порядка в общеалгебраической и канонической системе координат.
График в общеалгебраической системе координат:

График в канонической системе координат:
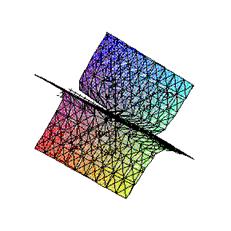
Вывод
Исследовав каноническое уравнение (4.7) гиперболического параболоида, отметим следующее:
1. Оси O'Z и O'X являются осями симметрии поверхности. Центра симметрии у поверхности нет.
2. Рассекая поверхность горизонтальными плоскостями Y = h, в сечениях получаем:
h > 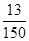 - гиперболы с действительными осями, параллельными оси O'Z
- гиперболы с действительными осями, параллельными оси O'Z
h = 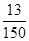 - две пересекающиеся прямые
- две пересекающиеся прямые
h < 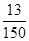 - сопряжённые гиперболы с действительными осями, параллельными оси O'Y
- сопряжённые гиперболы с действительными осями, параллельными оси O'Y
3. Рассекая поверхность плоскостями Z = h и X = h, в сечениях получаем параболы, с ветвями, направленными вниз (Z = h) или вверх (X = h).
4. Поверхность гиперболического параболоида бесконечна в направлении всех трёх координатных осей.
Список литературы
1. Копылова Т. В. Аналитическая геометрия. — Дубна: Международный университет природы, общества и человека «Дубна», 1997.
2. Ильин В. А., Позняк Г. Д. Аналитическая геометрия. — М.: Наука, 1974.